
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Деление Великого предела
|
|
В “Си цы чжуани” порождение символики “Книги перемен” описывается как последовательное дихотомическое деление Великого предела (тай цзи) — космической проявленной единичности — на взаимодополнительные полярности инь и ян:
В Переменах есть Великий предел (тай цзи).
Он рождает двоицу образов (и).
Двоица образов рождает четыре символа (сян).
Четыре символа рождают восемь триграмм (гуа).
Восемь триграмм определяют счастье и несчастье.
Счастье и несчастье рождают великое деяние (Си цы, I, 11).
В качестве графических символов принципов инь и ян в китайской арифмосемиотике используются знаки- и (“образы”) — соответственно прерывистая, “сломанная” (чжэ) и сплошная, “одинарная” (дань) черты (яо) (рис. 1.2.1).

Рис. 1.2.1
Точно не известно, когда появилась такая символика, но к ханьскому времени она уже имеет широкое распространение. Также неизвестно, каким способом обозначались полярные принципы в “Книге перемен” при ее возникновении. Возможно, это были числовые обозначения, о которых будет сказано ниже.
Инь и ян могут рассматриваться как относительно отдельные единичности (своего рода “локальные” Великие пределы). Они, в свою очередь, также разделяются на противоположности. Получаются уже четыре принципа, которые символизируются знаками, представляющими собой различные сочетания прерывистых и сплошных черт по две. Эти диграммы называются сян (“символы”). Диграммы, одна из которых состоит только из прерывистых черт, а другая — из сплошных, именуются соответственно “большими” (тай) инь и ян. Два других символа, состоящие из разных черт, — это “малые” (шао) инь и ян. В первом случае в верхней позиции находится прерывистая черта, а во втором — сплошная (рис. 1.2.2).
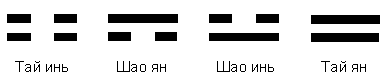
Рис. 1.2.2
Следующий шаг развертки приводит к образованию восьми знаков гуа, составленных из комбинирующихся черт, которые находятся в трех позициях. В китаеведении эти знаки принято называть “триграммами” (рис. 1.2.3).
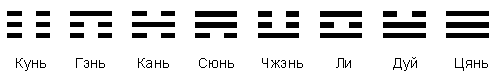
Рис. 1.2.3
Триграммы наделяются теми или иными корреляциями, из которых только часть зафиксирована в “Крыльях”, а именно в “Шо гуа чжуани”. Среди них очень важными являются корреляции с природными “феноменами” — “образами”, которые в китайских текстах часто используются в качестве замены названий триграмм. Для примера можно еще указать на корреляции триграмм с разновидностями животных, частями человеческого тела и направлениями в пространстве (табл. 1.2.1).
| Таблица 1.2.1 | ||||||||
| Название | Цянь | Дуй | Ли | Чжэнь | Сюнь | Кань | Гэнь | Кунь |
| Природные “феномены” | Небо | Низина | Огонь | Гром | Ветер | Вода | Гора | Земля |
| Животные | конь | овца | фазан | дракон | курица | свинья | собака | корова |
| Части тела | голова | рот | глаза | ноги | бедра | уши | руки | живот |
| Направления по Вэнь-вану | СЗ | З | Ю | В | ЮВ | С | СВ | ЮЗ |
Другая часть корреляций триграмм, гораздо более обширная, разбросана по различным текстам, написанным в более поздние времена. Среди них имеется несколько интересных образцов, о которых еще будет сказано в подходящем месте.
Надо отметить, что триграммы представляют собой не просто символы, а определенного типа кодовые знаки, значения которых определяются наличием в них янских или иньских черт и их расположением в позициях. Позиции (вэй) в ицзинистике принято считать снизу вверх и соотносить с “тремя способностями” (сань цай) — Земля (ди), Человек (жэнь) и Небо (тянь) (рис. 1.2.4).

Рис. 1.2.4
Триграммы, имеющие во всех позициях одинаковые знаки, называются “старшими”. В “семейной” символике три янских черты — это “отец” (триграмма [далее — тр.] Цянь), а три иньских — “мать” (тр. Кунь). Они рассматриваются как принципы, порождающие остальные триграммы, подобно тому, как космические ян и инь — Небо и Земля — порождают Человека.
Восемь триграмм раскачивают друг друга, возбуждаясь громовыми раскатами и оплодотворяясь ветром и дождем.
Круговращаются Солнце и Луна — то холод, то жара.
Дао Цянь доводит до зрелости мужское.
Дао Кунь доводит до зрелости женское.
Цянь знает великое начало.
Кунь обеспечивает созревание вещей (Си цы, I, 1).
Остальные триграммы называются “младшими”, или “детьми”. Они также подразделяются на янские и иньские, что определяется их структурой. Во всех “младших” триграммах одна черта по знаку противостоит двум другим. Эта черта и будет определять полярность всего символа, как об этом пишется в “Си цы чжуани”:
В янских гуа больше инь.
В иньских гуа больше ян.
В чем причина этого?
Янские гуа — нечетные.
Иньские гуа — четные.
Как действует их дэ?
В янских [ гуа ] единица — государь, а двойки — подчиненные.
Это дао благородного человека.
В иньских [ гуа ] двойка — государь, а единицы — подчиненные.
Это дао маленького человека (Си цы, II, 3).
В данном отрывке гуа подразделяются на нечетные (цзи) и четные (оу), что является просто свойством принципов ян и инь. Учитывая, что ян символизируется единицей, а инь — двойкой, “младшие” триграммы будут состоять либо из одной единицы и двух двоек, либо из одной двойки и двух единиц. Поскольку, по ицзинистской теории, малочисленное главенствует над многочисленным, первые будут янскими, а вторые — иньскими. Суммарное символическое число для янских триграмм — 1 + 2 + 2 = 5, а для иньских — 2 + 1 + 1 = 4. Поэтому янские триграммы — нечетные, а иньские — четные. С другой стороны, можно предположить, что имеется в виду какой-то конкретный порядок триграмм, в котором соответствующие триграммы стоят на четных и нечетных позициях.
Итак, “сыновьями” будут три триграммы, имеющие только одну сплошную черту, а остальные — прерывистые. Сплошная черта в первой позиции — “старший сын” (тр. Чжэнь), во второй — “средний сын” (тр. Кань), в третьей — “младший сын” (тр. Гэнь). “Дочери” имеют только одну прерывистую черту и две — сплошных. Прерывистая черта в первой позиции — “старшая дочь” (тр. Сунь); во второй — “средняя дочь” (тр. Ли); в третьей — “младшая дочь” (тр. Дуй). Подробным образом это правило излагается в “Шо гуа чжуани”:
Цянь — это Небо, поэтому символизирует отца.
Кунь — это Земля, поэтому символизирует мать.
Чжэнь — это предпочтение в первой [черте], являющейся мужской, поэтому символизирует старшего сына.
Сюнь — это предпочтение в первой [черте], являющейся женской, поэтому символизирует старшую дочь.
Кань — это предпочтение во второй [черте], являющейся мужской, поэтому символизирует среднего сына.
Ли — это предпочтение во второй [черте], являющейся женской, поэтому символизирует среднюю дочь.
Гэнь — это предпочтение в третьей [черте], являющейся мужской, поэтому символизирует младшего сына.
Дуй — это предпочтение в третьей [черте], являющейся женской, поэтому символизирует младшую дочь (Шо гуа, 9).
Видимо, именно этот порядок и имелся в виду, когда говорилось о четности и нечетности триграмм. В нем янские и иньские триграммы чередуются при последовательном расположении “по старшинству”: взрослые, а затем старшие, средние и младшие дети. Наиболее значимые порядки восьми триграмм, о которых будет сказано в дальнейшем, не имеют непрерывного чередования по принципу ян-инь. В “Шо гуа чжуани” приводятся еще три полных порядка и один без “старших” триграмм, но только в двух из них чередуются янские и иньские триграммы, причем более ясной закономерности, чем распределение “по старшинству”, в этих порядках не наблюдается (табл. 1.2.2).
| Таблица 1.2.2 | |||||
| № | § 3 | § 4 | § 4 | § 5 | § 6-17 |
| Цянь | Чжэнь | Чжэнь | Чжэнь | Цянь | |
| Кунь | Сюнь | Сюнь | Сюнь | Кунь | |
| Гэнь | Кань | Ли | Ли | Чжэнь | |
| Дуй | Ли | Кунь | Дуй | Сюнь | |
| Чжэнь | Гэнь | Дуй | Кань | Кань | |
| Сюнь | Дуй | Цянь | Гэнь | Ли | |
| Кань | Цянь | Кань | — | Гэнь | |
| Ли | Кунь | Гэнь | — | Дуй |
Триграммы, противоположные по “полу” и одного “возраста”, можно рассматривать как “дополнительные”. У них в одних и тех же позициях имеются различные черты, и эти триграммы можно преобразовывать друг в друга при помощи инверсии черт, или “противоположности” (дуй). Есть еще триграммы, которые образуются одна из другой при помощи “переворачивания” (фань). Это “старшие” и “младшие” триграммы одного “пола” (тр. Чжэнь — Гэнь; Сунь — Дуй). Остальные триграммы при этой операции не модифицируются, так как у них в нижней и верхней позициях имеются одинаковые черты, иначе говоря, они симметричны относительно средней позиции (рис. 1.2.5).
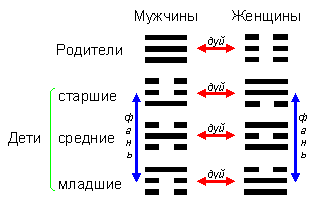
Рис. 1.2.5
Две полярности инь и ян символизируются, как уже говорилось, прерывистыми и сплошными чертами. Но реальные мировые полярности переходят друг в друга. Значит, и черты также должны преобразовываться одна в другую. Чтобы обозначить это их свойство, в китайской арифмосемиотике вводятся еще два дополнительных символа. Один из них должен обозначать прерывистую черту, превращающуюся в свою противоположность, т.е. в черту, у которой две половинки соединяются (®), — “сплетающуюся” (цзяo). А другой обозначает сплошную черту, разрывающуюся на две половинки (®), — “раздваивающуюся” (чун). Эти два символа называются “старыми” (лао), в отличие от предыдущих, называемых “молодыми” (шао). “Старый ян ” может обозначаться кружочком и числом 9, а “старая инь ” — диагональным крестиком и числом 6 (рис. 1.2.6). “Молодые” ян и инь имеют числовую символику 7 и 8. Динамика взаимодействий всех четырех принципов выражается следующим образом: “молодые” черты “стареют”, т.е. превращаются в “старые” черты, не меняя знака, а “старые” уже его меняют, “умирая” и превращаясь в противоположные “молодые” черты, которые вновь “стареют”, и т.д.

Рис. 1.2.6
То же самое можно сказать о символизации космической динамики с помощью диграмм (рис. 1.2.7). “Малые” инь и ян, “вырастая”, становятся соответственно “большими” инь и ян, а те, “умирая”, “возрождаются” в качестве “малых” ян и инь.
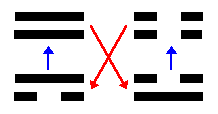
Рис. 1.2.7
Для триграмм ситуация немного усложняется, поскольку “младшие” триграммы, прежде чем “постареть”, должны последовательно пройти три “возрастных” состояния — “младшее”, “среднее” и “старшее” (рис. 1.2.8).

Рис. 1.2.8
Числовые символы черт — 6, 7, 8, 9 — используются при гадании. Эти числа получаются при пересчете специальных палочек, изготовленных из стеблей тысячелистника, или при подсчете суммы чисел, являющихся символами лицевой и оборотной сторон монет, с помощью которых производится гадание. Те же числовые символы можно соотнести с триграммами, учитывая, что входящие в них иньские черты обозначаются числом 2, а янские — 3. Таким образом, 6 и 9 символизируют “старшие” триграммы, а 7 и 8 — “младшие”, причем нечетные из этих чисел символизируют “мужские” триграммы, а четные — “женские” (рис. 1.2.9).

Рис. 1.2.9
Все рассмотренные символы, т.е. и, сян и гуа, можно представить на одном общем чертеже, выражающем собой процесс развертки Великого предела (рис. 1.2.10).

Рис. 1.2.10
Получается нечто вроде “дерева”, при ветвлении которого в символах каждого следующего уровня добавляется новая верхняя позиция с той или иной чертой. Можно составить более простую схему, в которой Великий предел находится внизу, и новый ряд символов получается при добавлении верхней позиции к символам предыдущего ряда (рис. 1.2.11).

Рис. 1.2.11
Подобным образом строится чертеж “Тай цзи”, в котором янские и иньские силы изображаются светлой и темной полосами (рис. 1.2.12).

Рис. 1.2.12
Триграммы в данном случае покоятся на основании “Великого предела” (тай цзи), который символизируется янской, светлой полосой. Таким образом, они, по сути, являются тетраграммами, что становится очевидным, если к данному набору символов добавить сходный набор, но имеющий в основании “Беспредельное” (у цзи), которое будет символизироваться темной полосой.
В принципе, наращивать позиции символов в таких схемах можно до бесконечности, но древние китайцы остановились на 6-ти позициях. Символика с 4-мя и 5-ю позициями не употреблялась, а шестеричные символы занимали очень важное место в древнекитайской науке, поскольку они составляли символическую основу “Книги перемен”. Их называли так же, как и триграммы, — гуа (в китаеведении используется термин “гексаграммы”). Всего таких символов 64, т.е. полное число вариантов, получаемых при комбинировании двух типов черт в 6-ти позициях или при сочетании по две всех триграмм, составляющих верхние и нижние части гексаграммы.
Несмотря на то, что структура вышеприведенного чертежа Великого предела основывается на тексте из “Си цы чжуани”, этот чертеж стал известен в Китае только в XI в., когда его обнародовал неоконфуцианский философ Шао Юн (1011—1077). Он ссылался на “Си цы чжуань” как на идейный источник и, кроме того, утверждал, что эта схема принадлежала Фуси. В связи с этим зафиксированный в схеме порядок триграмм стал называться “порядком Фуси”.
Нетрудно заметить, что этот порядок отражает некоторые закономерности двоичного счисления, т.е. способа выражения чисел с помощью двух цифр — “0” и “1”, открытого известнейшим немецким философом и математиком Готфридом Лейбницем (1646—1716)в конце XVII в. Действительно, если обозначить прерывистую черту как “0”, а сплошную — как “1”, то окажется, что получившиеся трехразрядные двоичные символы располагаются на схеме в порядке чисел от 0 до 7 (рис. 1.2.13). Однако такое совпадение, конечно, не означает, что древние китайцы знали двоичный счет. Для построения порядка Фуси достаточно логики схемы, которую предложил Шао Юн. В ней же зафиксирован прежде всего строгий метод двоичной комбинаторики.
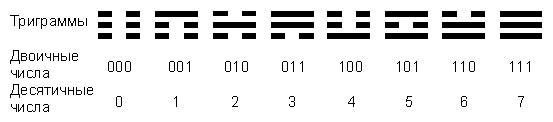
Рис. 1.2.13
Интересно, что Лейбниц через несколько лет после своего открытия, а именно в 1701 г., получил письмо от своего друга, миссионера в Китае патера Иоахима Буве, из которого узнал о существовании древней системы символов “Книги перемен”, сходной с его двоичным счетом. Это возбудило в нем чрезвычайный интерес к данной книге. Он даже делал попытки объяснить содержащуюся в ней символику с помощью двоичной арифметики (см.: Лейбниц 1999: 108—110; Швырев 1987: 145—147).
Следует отметить, что Шао Юн — не первый, кто использовал порядок Фуси. Этот неоконфуцианец только указал на один из способов его построения. В начале X в. круговую схему с порядком Фуси составил даос Чэнь Туань, дав ей название “преднебесный чертеж” (сянь тянь ту) и также приписав ее Фуси. Чэнь Туаню принадлежит и ориентация этой схемы по странам света (рис. 1.2.14; по китайским канонам “юг” было принято изображать сверху).

Рис. 1.2.14
В этой схеме порядок Фуси образуется из двух последовательностей по четыре триграммы, которые соединяются через центр круга (отмечено пунктиром; триграммы основанием обращены к центру круга, который с космологической точки зрения ассоциировался с Землей).
Существовала еще одна круговая схема с триграммами, более древняя, чем предыдущая (рис. 1.2.15). В виде орнамента ее можно увидеть уже на ханьских бронзовых зеркалах. Эта схема основывалась на корреляциях триграмм со странами света, зафиксированных в “Шо гуа чжуани”. Схема приписывалась Вэнь-вану и имела название “посленебесный чертеж” (хоу тянь ту).

Рис. 1.2.15
Наборы гексаграмм
Гексаграммы также имеют канонизированные порядки расположения, связанные с именами Фуси и Вэнь-вана. В первом случае порядок гексаграмм образуется при комбинировании в составе гексаграмм верхних и нижних триграмм, располагающихся в порядке Фуси. Существуют табличная, или “квадратная” (фан ту фан вэй), и круговая (юань ту фан вэй) записи этого порядка гексаграмм. Квадратная запись достаточно наглядно отражает принцип комбинирования триграмм (рис. 1.2.16).

Рис. 1.2.16
При круговой записи, которая подобна круговому расположению триграмм в порядке Фуси, первая половина всего набора гексаграмм располагается на круге против часовой стрелки, а вторая — по часовой стрелке.
В случае гексаграммного порядка Вэнь-вана, имеющего также табличную (рис. 1.2.17) и круговую записи, общую закономерность расположения гексаграмм синологам пока найти не удалось, хотя и совершалось немало попыток. Ничего общего с триграммным круговым порядком Вэнь-вана этот порядок не имеет, за исключением того, что оба приведены в “Чжоу и”. Именно в порядке под этим названием гексаграммы располагаются в основной части данного текста. Единственный и достаточно очевидный принцип связи гексаграмм, обнаруженный пока в этом порядке, заключается в том, что они группируются в пары по принципу переворачивания (фань), а там, где переворачивание приводит к исходной гексаграмме, — по принципу дополнительности (дуй).

Рис. 1.2.17
При археологических раскопках, проводившихся в 1973 г. в местечке Мавандуй (рядом с г. Чанша в пров. Хунань), был обнаружен самый древний экземпляр “Книги перемен”, датируемый 180—170 гг. до н.э. (см.: Вэнь у 1984: 1—8). В этом тексте гексаграммы располагаются в порядке, который у синологов получил название “мавандуйский” (рис. 1.2.18).

Рис. 1.2.18
Алгоритм данного порядка достаточно прост. Весь набор гексаграмм подразделяется на восемь серий, в которых имеются одинаковые верхние триграммы. Последовательность смены серий с данными триграммами соответствует их ранжированию по “семейным” характеристикам: отец, младший, средний и старший сыновья, мать, младшая, средняя и старшая дочери. Последовательность нижних триграмм построена по принципу дополнительности, совмещаемому со старшинством: отец и мать, младшие, средние и старшие сыновья и дочери (рис. 1.2.19).

Рис. 1.2.19
Сочетания верхних и нижних триграмм в данных последовательностях приводят к образованию восьми серий гексаграмм, в которых затем осуществляется перестановка определенных гексаграмм в начало серии. Для перестановки берутся “чистые” (чунь) гексаграммы, т.е. составленные из одинаковых триграмм и имеющие их названия. В первой серии данная перестановка не требуется или может считаться чисто номинальной, поскольку в ее начале стоит как раз такая гексаграмма.
Еще один способ группировки гексаграмм — по “дворцам” — зафиксирован в сочинении раннеханьского ицзиниста Цзин Фана (77—33) “Цзин-ши и чжуань” (“Комментарий г-на Цзина к [Книге] перемен”). В основе построения системы “дворцов” лежит принцип поочередного изменения черт в позициях. Каждый дворец задается “чистой” гексаграммой. Поскольку таких гексаграмм восемь, то и дворцов тоже восемь (рис. 1.2.20).

Рис. 1.2.20
В каждом “дворце” каждая из пяти гексаграмм, находящихся после “чистой”, отличается от предыдущей только одной чертой, причем изменение черт происходит снизу вверх. Последняя в этом списке гексаграмма совпадает с “чистой” только верхней чертой. Ее изменение привело бы к переходу в другой дворец. Такими сцепленными дворцами, охватывающими в сумме 48 гексаграмм, являются дворцы Цянь и Кунь, Дуй и Гэнь, Ли и Кань, Чжэнь и Сюнь. В них в соответствующих местах стоят инвертные гексаграммы.
Оставшиеся 16 гексаграмм не подчиняются указанным закономерностям. Эти гексаграммы невозможно связать между собой посредством последовательного изменения одной черты. К первым шести гексаграммам в каждом дворце они подстраиваются за счет смены одной черты, но при этом нарушается предыдущий порядок переходов от позиции к позиции. При переходе в каждом дворце от шестой к седьмой гексаграмме изменяется четвертая снизу черта. Восьмые гексаграммы отличаются от первых пятой позицией. Между седьмой и восьмой гексаграммами различие образуется за счет инвертирования нижней триграммы.
Седьмые и восьмые гексаграммы в каждом дворце имеют особые названия. Они называются соответственно гексаграммами “странствующей души” (ю хунь) и “возвращающими душу” (гуй хунь). Как указывает Чжоу Цзунхуа, когда эти гексаграммы выпадают при гадании, это считается плохим предзнаменованием (Чжоу Цзунхуа 1996: 118). Судя по названиям и сопутствующим текстам, половина из них имеет положительные, а другая половина — отрицательные значения. Поэтому следует сделать уточнение. Негативный смысл все они, вероятно, приобретают в определенных случаях гадания, когда получаются две гексаграммы за счет изменения “подвижных” (бянь) черт. Исходная гексаграмма называется гуй хунь, если у нее изменяется только пятая черта, что приводит к образованию “чистой” гексаграммы. Если первая — гуй хунь, а вторая образуется за счет инверсии нижней триграммы, то она оказывается ю хунь.
Date: 2016-08-30; view: 467; Нарушение авторских прав