Минимизация функции нескольких переменных

Для поиска минимума функции нескольких переменных применяется команда fminsearch.

Использование команды продемонстрируем на примере нахождения локального минимума функции f(x,y)=sinsin, зависящей от двух переменных x и y. Сначала получим представление о поведении функции, построив ее линии уровня при помощи следующих команд (рис. 6.4):

>> [X,Y]=meshgrid(0:.01:2);

>> Z=sin(pi/2*X.^2).*sin(pi/2*Y.^2);

>> [CMatr,h]=contour(X,Y,Z,[-.9,-.5,-.1,.1,.5,.9]);

>> clabel(CMatr,h)

На графике, приведенном на рис. 6.4, видно расположение локальных минимумов и максимумов. Один из локальных минимумов имеет стартовое приближение (1;1,7) в системе координат xOy.

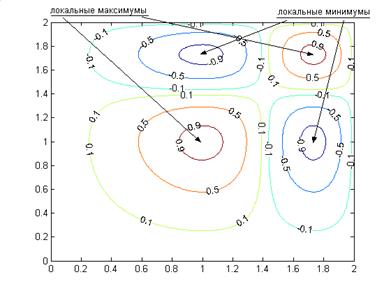
Рис. 6.4

Перед применением fminsearch необходимо создать файл-функцию, вычисляющую значения данной функции, причем аргументом файл-функции должен быть вектор, первый элемент которого соответствует переменной х, а второй – y. Приведем текст требуемой файл-функции:

function f=gr2(arg)

x=arg(1);

y=arg(2);

f=sin(pi/2*x.^2).*sin(pi/2*y.^2);

Теперь для уточнения координат точки минимума вызовем fminsearch с двумя входными аргументами – указателем на файл-функцию gr2 и стартовым приближением (1;1,7). В результате выходной аргумент – вектор M, возвращает координаты искомой точки минимума:

>> M=fminsearch(@gr2,[1,1.7])

M =

1.0000 1.7320

Для получения значения функции в точке минимума следует вызвать fminsearch с двумя выходными аргументами:

>> [M,f]=fminsearch(@gr2,[1,1.7])

M =

1.0000 1.7320

f =

-1.0000

Команды fzero, fsolve, fminbnd и fminsearch позволяют задать дополнительный параметр options, контролирующий вычислительный процесс. Значение options следует предварительно сформировать при помощи команды optimset в соответствии с характером требуемого контроля.

В разделе 6.3 найдено приближенное значение локального минимума функции e^-xcos2πx. Представим результат в формате вывода long:

>> format long

>> [x2,f]=fminbnd(@gr,1.4,1.6)

x2 =

1.47489614357390

f =

-0.22596214557056

Задание максимальной точности eps нахождения локального минимума осуществляется при помощи следующих команд:

>> options=optimset('TolX',eps);

>> [x2,f]=fminbnd(@gr,1.4,1.6,options)

x2 =

1.47488038336724

f =

-0.22596214670612

Здесь eps – системная переменная MATLAB (см. разд. 1.2):

>> disp(eps)

2.220446049250313e-016

Аналогичным образом точность задается при нахождении корней и минимизации функции нескольких переменных. Об остальных параметрах команды optimset можно узнать с помощью команды doc optimset.

В следующем разделе проводится сравнение результатов вычислений с различной заданной точностью.

Date: 2016-08-30; view: 233; Нарушение авторских прав