Каркасные поверхности

Команда plot3(…) может быть использован для построения так называемой каркасной поверхности, которая ограничивает поверхность геометрического тела и похожа на каркас, сплетенный из проволоки.

Пример 16. Построить график каркасной поверхности функции z(x,y) = x+y³ (рис. 5.18), где переменные x и y изменяются на интервале [ – 8;8] с шагом 1. Для построения графика использовать непрерывные линии. Линии, расположенные параллельно плоскости zOy, закрасить в черный цвет, а линии, параллельные плоскости zOx – в красный цвет. На плоскостях xOy, zOx, zOy сформировать сетку.

>> [x,y]=meshgrid(-8:8);

>> z=x+y.^3;

>> plot3(x,y,z,'k',y,x,z,'r')

>> grid on

Как видно из текста программы, для формирования каркасной поверхности в команде plot3(…) использованы два аргумента с дополнительными параметрами. При этом во втором аргументе переменные x и y переставлены местами. Сетка, как и в 2D графике, задается командой grid on.

Рис. 5.18

В примере 16 для построения каркасной поверхности была использована команда plot3(…). Однако для построения таких поверхностей в MATLAB имеются и другие команды, например, mesh(…) и surf(…).

Пример 17. С помощью команды mesh(…) построитькаркасную поверхность (рис. 5.18), заданную функцией z = sin(x)/(x²+y2+0,3), где переменные x и y изменяются на интервале [ – 3;3] с шагом 0,1.

>> [x,y]=meshgrid(-3:0.1:3);

>> z=sin(x)./(x.^2+y.^2+0.3);

>> mesh(x,y,z)

На экране цветного монитора можно видеть, что цвет линий каркасной поверхности зависит от величины значений функции z. Кроме того, команда mesh(…) предполагает вывод только видимой части поверхности.

Рис. 5.19

Для того чтобы сделать каркасную поверхность «прозрачной» (рис. 5.20), следует использовать команду hidden off. Предыдущая программа в этом случае имеет вид

>> [x,y]=meshgrid(-3:0.1:3);

>> z=sin(x)./(x.^2+y.^2+0.3);

>> mesh(x,y,z)

>> hidden off

Рис. 5.20

Команда hidden on убирает невидимую часть поверхности, возвращая графику прежний вид.

В отличие от команды mesh(…) применение команды surf(…) позволяет окрасить не только линии графика, но и залить определенным цветом каждую клетку поверхности. Цвет зависит от значений функции в точках, соответствующих углам клетки.

Результат замены команды mesh(x,y,z) в примере 17 на команду surf(x,y,z) представлен на рис. 5.21.

Рис. 5.21

Трехмерные графики, изображенные на рис. 5.19 – 5.21, позволяют наглядно представить форму поверхности, однако по ним трудно судить о значениях двухмерной функции. Для того чтобы частично устранить этот недостаток, можно после команды surf(x,y,z) применить команду colorbar, которая выводит рядом с графиком столбик, устанавливающий соответствие между цветом поверхности и величиной функции. Рис. 5.22 иллюстрирует получающийся результат.

Рис. 5.22

Команду colorbar можно использовать в сочетании со всеми операторами MATLAB, строящими трехмерные объекты.

Применение после команды surf(x,y,z) команды shading flat позволяет убрать каркасные линии (рис. 5.23), а использование команды shading interp – получить поверхность, плавно залитую цветом, зависящим от значений функции.

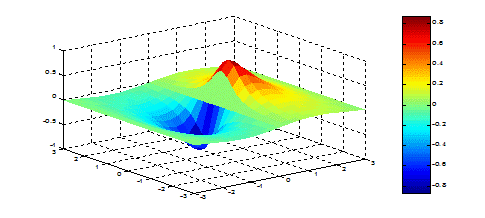
Рис. 5.23

Контурные графики

Контурные графики, как правило, представляют собой некоторый набор линий на плоскости. Каждая из линий является горизонтальной проекцией линии пересечения заданной поверхности с плоскостью горизонтального уровня.

MATLAB позволяет получить различные типы контурных графиков при помощи команд contour(…) и contourf(…).

Пример 18. Построить контурный график функции z = x²+y² (рис. 5.24) из 20 линий. Переменные x и y изменяются на интервале [ – 3;3] с шагом 0,1.

>> [x,y]=meshgrid(-3:0.1:3);

>> z=x.^2+y.^2;

>> contour (x,y,z,20)

>> colorbar

Рис. 5.24

Такой контурный график дает весьма приблизительное представление о том, какое значении функции соответствует той или иной линии уровня.

MATLAB позволяет нанести на каждую линию уровня, значение, которое принимает на ней исследуемая функция. Для этого служит команда clabel (…).

Команда clabel(…) вызывается с двумя аргументами: матрицей, содержащей информацию о линиях уровня, и указателем на график, где следует нанести числовое значение функции.

Пользователю необязательно самому создавать аргументы clabel (…). Для этого команду contour(…) следует вызвать с двумя выходными аргументами.

Поясним это на примере.

Пример 19. Построить контурный график функции z = x²+y² (рис. 5.25), состоящий из 10 оцифрованных линий уровня. Переменные x и y изменяются на интервале [ – 3;3] с шагом 0,1.

>> [x,y]=meshgrid(-3:0.1:3);

>> z=x.^2+y.^2;

>> [C,H]=contour (x,y,z,10);

>> clabel(C,H)

>> grid on

Рис. 5.25

MATLABпредоставляет возможность оцифровки линий уровня вручную. Для этого вместо команды clabel(C,H) необходимо использоватькоманду clabel(C,H,’manual’). Такая замена в примере 19 приводит к тому, что на экран монитора выводится контурный график без оцифровки линий уровня, но с перекрестьем, которое можно двигать по изображению с помощью мыши. Расположив перекрестье на требуемой линии уровня и нажав левую или правую кнопку мыши, можно получить значение функции, соответствующее выбранной линии. Для того, чтобы завершить оцифровку линий уровня, перекрестье следует поместить за пределы графика и нажать любую кнопку мыши.

На рис. 5.26 представлен результат оцифровки с помощью команды clabel(C,H,’manual’) четырех линий уровня, рассчитанных применительно к условиям примера 19.

Рис. 5.26

MATLABпозволяет строить линии уровня не только на плоскости, но и на графике двухмерной функции z(x,y). Для этого применяется команда surfc(x,y,z), правила использования которого аналогичны правилам для команды surf(x,y,z).

Если в примере 17 для вывода графика сделать замену команды mesh(x,y,z) на команду surfc(x,y,z), то получим результат, показанный на рис. 5.27.

Рис. 5.27

Date: 2016-08-30; view: 274; Нарушение авторских прав