Представление функции в виде дискретных отсчетов

Представить графическую зависимость в виде дискретных отсчетов можно, пользуясь командой stem(…). В общем случае команда stem(…) имеет вид stem(t,y,S), где S является дополнительным параметром, который используется так же, как и в команде plot(…). Параметр S выбирается из таблицы 5.1.

stem(Y) – строит зависимость значений элементов вектора от номеров этих значений в виде дискретных отсчетов.

Пример 8. Построить график функции y(t) = e^-tsin(10t), где аргумент t меняется от 0 до 1 с шагом 0,02. Функцию у задать как вектор (рис. 5.10).

>> t=[0:0.02:1];

>> Y=exp(-t).*sin(10*t);

>>stem(Y)

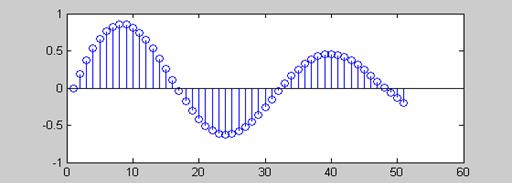
Рис. 5.10

Цвет и стиль линии, а также форму маркера на рис. 5.9 система MATLAB выбрала самостоятельно.

Пример 9. Построить график функции y(t) = e^-tsin(10t), где аргумент t меняется от 0 до 1 с шагом 0,02 (рис. 5.11). Дискретные отсчеты закрасить красным цветом, обозначить маркером в виде * и вычертить штриховой линией.

>> t=[0:0.02:1];

>> Y=exp(-t).*sin(10*t);

>> stem(t,Y,'r*--')

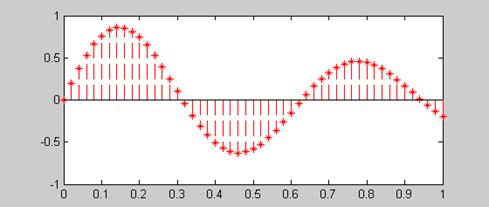
Рис. 5.11

Обратите внимание на то, чем отличается на графиках рис. 5.10 и рис. 5.11 шкала оси абсцисс. На рис. 5.10 значения оси абсцисс представляют собой целочисленный ряд 0, 1, 2, …, 50, т.е. соответствуют номерам элементов вектора Y, а на рис. 5.11 значения абсцисс представляют собой определенную на интервале [0;1] и возрастающую с шагом 0,02 последовательность действительных чисел.

Лестничные графики

Лестничные графики представляют собой ступеньки с огибающей, заданной в виде функции y(t). Они используются, например, для наглядного представления функции y(t), представленной результатами ряда измерений ее значений. При этом в промежутках между измерениями значения функции считаются постоянными и равными величине последнего результата измерения.

Для построения лестничных графиков используется команда stairs(…). Общий вид аргумента команды stairs(…) – такой же, как и в командах plot(…) и stem(…). Правила использования дополнительного параметра S аналогичны правилам, применяемым для команд plot(…) и stem(…).

Пример 10. Построить лестничный график функции y(t) = e^0,1t, где аргумент t меняется от 0 до 20 с шагом 1 (рис 5.12). Описание дополнительного параметра S (см. табл. 5.1): цвет – зеленый, тип маркера – «квадрат», стиль линии – пунктирная.

Программу для расчета значений функции у(t) и вывода требуемого графика (рис. 5.12) представим в двух вариантах:

Вариант 1 Вариант 2

t=[0:20]; t=[0:20];

y=exp(0.1*t); stairs(t,exp(0.1*t),'gs:')

stairs(t,y,'gs:')

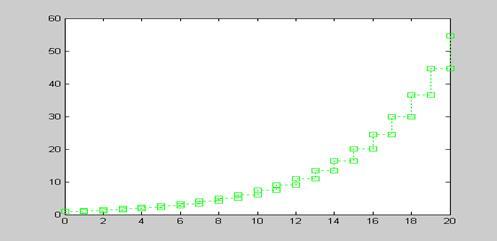
Рис. 5.12

Программа в варианте 2 на одну строку короче. MATLAB может вычислять значения у(t) не только предварительно, но и непосредственно при использовании команды stairs(…). Это оказывается верным также и в случаях применения команд plot(…), stem(…) и команды errorbar(…), которая рассматривается ниже.

Date: 2016-08-30; view: 286; Нарушение авторских прав