Основная теорема линейной регрессии.

Пусть есть Х и У выборки объема Т.

1)

2) - детерминированное (т.е. случайная величина)

3) а)

б) или к нормальной линейной регрессии

Оценк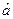и и получены методом наименьших квадратов, являются лучшими в классе линейных несмещенных оценок, т.к. обладают наименьшей дисперсией.

Замечание: наши оценки являются наилучшими, если мы оцениваем модель, линейную по параметру.

Пример: - линейная модель, т.к. ,

или - линейная модель по параметру

-нелинейная модель

Замечание: остатки после построения регрессии должны иметь нормальное распределение с параметрами математическое ожидание=0 и дисперсия=0, т.е., оценив регрессию, мы должны проверить остатки на нормальность.

Оценив параметры модели, мы хотим узнать, насколько точно мы оценим коэффициент. Точность оценки связана с ее дисперсией.

Поэтому найдем дисперсию 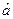и . Для простоты расчетов введем обозначения:

Тогда дисперсия оценки 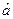будет равна:

Теперь у нас есть наилучшие оценки коэффициентов регрессии aи b, однако в регрессионном уравнении есть еще один неизвестный параметр – это дисперсия ошибок .

Из этих двух формул следует, что чем больше измерений, тем точнее результат и меньше дисперсии.

Рассмотрим дисперсию ошибок более подробно.

Обозначим через - прогноз в точке

Тогда остатки моделей будут собой представлять разницу между истинными и прогнозируемыми значениями.

- случайные величины, но - остатки, 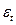- ошибки

Но остатки в отличие от ошибок ненаблюдаемы, поэтому для оценки дисперсии ошибок проще рассмотреть ее через остатки.

Попробуем выразить дисперсию ошибок через остатки модели.

Поскольку математическое ожидание у ошибок и остатков нулевое, то дисперсия выражается через математическое ожидание суммы:

- неизвестная дисперсия остатков

Замечание: неизвестная дисперсия остатка связана с количеством наблюдений (их должно быть как можно больше) и с ошибками (они должны быть как можно меньше). Поэтому из двух подобранных моделей мы выбираем ту, которая точнее строит прогнозы даже если она построена по выборке объемом с меньшим Т.

Date: 2016-08-29; view: 286; Нарушение авторских прав