Модель парной линейной регрессии

Раздел I

Анализ невременных данных

Мы будем работать с данными, которые не являются временными, т.е. их можно переставлять местами, не меняя смысла

Случайная величина (с.в.) x – это числовая функция, заданная на некотором вероятностном пространстве.

Функция распределения с.в. x– это числовая функция числового аргумента, заданная равенством: F(x)=P(x C)

Характеристики случайной величины

I. Математическое ожидание с.в. x.

Обозначается E(x). Показывает среднее ожидаемое значение.

Если x – дискретная с.в., то

Если x – непрерывная с.в., то , где f(x) – плотность распределения.

Т.к. при работе с данными мы не знаем вероятности, то математическое ожидание считается как , где n – количество наблюдений

Свойства математического ожидания:

1) , где x и y – с.в.; a и b = const

2)

3) Если с.в. y 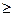с.в. x, то

4) Если , то

II. Дисперсия

Обозначается D[x]=V(x). Дисперсия – это среднее отклонение от среднего, т.е. на сколько в среднем большинство значений отклонится от математического ожидания, т.е. большинство значений будет лежать в интервале:

Свойства дисперсии:

1)

2)

3)

III. Ковариация

Обозначается Cov(x,y). Показывает однонаправленность двух случайных величин, т.е. ковариация – это мера линейной зависимости с.в.

Свойства ковариации:

1)

2)

3)

4)

Т.к. ковариация меняется от до , то использовать ее как меру линейной связи, неудобно, поэтому вводят понятие корреляции.

IV. Корреляция.

Обозначается Corr(x,y). Показывает силу линейной связи в интервале

Свойства корреляции:

1)

2) Если , то между x и y связи нет.

3) Если , то связь сильная положительная, т.е. рост x вызывает рост y и наоборот.

Замечание: если , т.е. линейной связи нет, то это не значит, что нет нелинейной связи.

Ложная корреляция.

При использовании следует помнить, что он показывает наличие только линейной связи. Ложная корреляция – в ряде случаев неправильно выбраны случайные величины, между которыми ищется корреляционная связь.

Пример: Если искать связь между длиной волос и ростом, то получится, что чем выше человек, тем короче у него волосы. Ошибка в том, что следует рассматривать эту зависимость отдельно по мужчинам и отдельно по женщинам.

V. Медиана

Медиана – это альтернатива определения среднего значения. Она считается по упорядоченному по возрастанию ряду из наблюдений (вариационный ряд). Показывает среднее из большинства. Обозначается med.

Пример: Имеются 10 человек. 9 человек получают 100$, 1 – 10000$. Найти средний доход человека.

Средний доход человека

Мы видим, что среднее значение малоэффективно и не показывает реальной ситуации.

Используем медиану.

1)

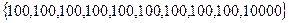
2) т.к. Т=10, то

Медиана показала реальное положение вещей.

Медиана используется, когда есть несколько сильных выбросов, т.е. несколько резко выделяющихся от других значений.

VI. Мода.

Мода – это число, делящее выборку пополам, т.е. 50% значений лежит выше нее, а 50% - ниже. Обозначается mod.

Пример:

Медиана показывает насколько справедливо среднее.

VII. Оценки

Введем обозначения:

истинное значение параметра

оценка параметра

Т.к. истинное значение параметра неизвестно, то мы его находим (оцениваем) по некоторой выборке объема Т.

то число, которое скорее всего примет истинное значение.

Свойства оценок:

Мы стараемся найти и подобрать выборку таким образом, чтобы по ней получить оценки, которые:

1) состоятельны, т.е. при оценка стремится к истинному значению, т.е., чем больше выборка, тем точнее оценка

2) несмещенность, т.е. математическое ожидание оценки – это истинное значение, т.е. в среднем мы получаем истинное значение

3) эффективность, т.е. дисперсия оценки – минимальна

Замечание: дисперсия напрямую связана с точностью оценивания. Чем выше дисперсия, тем больше варьируемость признака, тем менее точный результат мы получаем.

Модель парной линейной регрессии

Пусть Y,X – две выборки объема Т.

Возникает вопрос. Связаны ли они между собой? Если да, то как, и как выразить эту связь количественно?

У

Х

Необходимо подобрать а и bтакими, чтобы линия была как можно ближе ко всем значениям. a иb – неизвестные параметры. Необходимо подобрать a иb, минимизировав меру расстояния от точек, до получившейся прямой. В качестве меры можно взять сумму квадратов отклонения от среднего

Т.е. мы суммируем квадраты расстояния в каждой точке между наблюдаемым значением и тем, что лежит на линии. Берется квадрат расстояний, чтобы большим расстояниям придать больший вес, а также избежать отрицательных значений.

Иногда в качестве меры отклонения берут модуль расстояния

Но вычисления с модулем гораздо сложнее. Мы будем использовать квадрат отклонений.

Для нахождения неизвестных параметров а и b, имея в распоряжении выборки Y и X объема Т, нам необходимо минимизировать следующее расстояние

Мы ищем линию, которая будет максимально близко лежать от этих точек.

Применяя метод Лагранжа в решении подобных задач, получаем что:

,

где

Мы получили оценки неизвестных параметров a и b, удовлетворяющие свойствам оценок, с помощью которых можно построить уравнение регрессии и найти качественную зависимость между X и Y.

, ,

- вектор из двух букв a и b.

В данном случае построить регрессию, значит найти оценку вектора .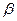

- матричная форма записи

Date: 2016-08-29; view: 273; Нарушение авторских прав