
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Алгоритм решения транспортной задачи методом потенциалов.
|
|
1. Проверяют выполнение необходимого и достаточного условия разрешимости задачи. Если задача имеет неправильный баланс, то вводят фиктивного поставщика или потребителя с недостающими запасами или запросами и нулевыми стоимостями перевозок.
2. Строят начальное опорное решение (методом северо – западного элемента, минимального элемента или методом Фогеля).
3. Опорный план проверяется на условие «вырождения». Согласно теореме Данцига количество занятых клеток в плане не должно превышать суммарного числа строк и столбцов минус единицу  (Для дальнейшего решения необходимо добиться того, чтобы количество занятых клеток в плане в точности равнялось суммарному числу строк и столбцов минус единица
(Для дальнейшего решения необходимо добиться того, чтобы количество занятых клеток в плане в точности равнялось суммарному числу строк и столбцов минус единица  , этого можно добиться вводя при необходимости нулевые перевозки, т.е. заполняя некоторые клетки нулями), где Кз – число занятых клеток; n – число строк (пунктов отправления); m – число столбцов (пунктов назначения).
, этого можно добиться вводя при необходимости нулевые перевозки, т.е. заполняя некоторые клетки нулями), где Кз – число занятых клеток; n – число строк (пунктов отправления); m – число столбцов (пунктов назначения).
4. Строят систему потенциалов, соответствующих опорному плану. Для этого одной из строк, или одному из столбцов (обычно тому, которому соответствует большее число занятых клеток) присваивают произвольное значение «потенциал» (значение потенциала удобно брать больше, чем значение максимального тарифа) и через заполненные клетки, используя соотношение  +
+  =
=  (где
(где  – потенциал строки, а
– потенциал строки, а  – потенциал столбца), строят систему потенциалов, т.е. получают потенциалы всех строк и столбцов. (Поясним, что предложенная для построения системы потенциалов формула
– потенциал столбца), строят систему потенциалов, т.е. получают потенциалы всех строк и столбцов. (Поясним, что предложенная для построения системы потенциалов формула  +
+  =
=  позволяет по известной себестоимости товара в пункте отправления путем прибавления к ней тарифа за транспортировку определить себестоимость товара в пункте назначения, и обратно, преобразовав формулу
позволяет по известной себестоимости товара в пункте отправления путем прибавления к ней тарифа за транспортировку определить себестоимость товара в пункте назначения, и обратно, преобразовав формулу  –
–  =
=  по известной себестоимости товара в пункте назначения, становится возможным, вычтя тариф за транспортировку, определить себестоимость товара в пункте отправления. Еще раз отметим, что система потенциалов строится только через заполненные клетки.)
по известной себестоимости товара в пункте назначения, становится возможным, вычтя тариф за транспортировку, определить себестоимость товара в пункте отправления. Еще раз отметим, что система потенциалов строится только через заполненные клетки.)
5. Проверяют условие оптимальности  +
+ 
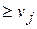 , это условие можно проверять только для свободных клеток таблицы, т.к. в заполненных оно всегда выполнено (Отметим, что невыполнение данного условия фактически означает возможность уменьшения себестоимости товара в пункте назначения, которое может быть достигнуто за счет перераспределения транспортных потоков).
, это условие можно проверять только для свободных клеток таблицы, т.к. в заполненных оно всегда выполнено (Отметим, что невыполнение данного условия фактически означает возможность уменьшения себестоимости товара в пункте назначения, которое может быть достигнуто за счет перераспределения транспортных потоков).
6. Если условие оптимальности выполнено для всех клеток матрицы, то нами получен оптимальный план перевозок (т.к. уменьшения себестоимости товара в пунктах назначения за счет перераспределения транспортных потоков невозможно) и необходимо только найти значение целевой функции L (X). Если же для какой-либо клетки условие оптимальности нарушается, то необходимо применить «формальное правило улучшения плана» и вернуться к пункту 3.
Формальное правило улучшения плана:
а) начиная с клетки, имеющей нарушение, двигаясь только по горизонталям и вертикалям, строится замкнутый контур с вершинами в занятых клетках;
б) начиная с клетки, имеющей нарушение, нумеруются вершины контура (направление обхода контура значения не имеет);
в) в четных вершинах контура находится значение минимальной перевозки;
г) для балансировки матрицы в нечетные вершины контура найденное значение прибавляется, из четных вершин – вычитается. Получается новый, улучшенный план.
Задача
Найдем оптимальное решение транспортной задачи опорный план которой представлен следующей транспортной матрицей:
| Пункты отправления, A i | Пункты назначения Bj | |||||||||
| B1 | B2 | B3 | B4 | Bф | ||||||
| A1 | ||||||||||
| A2 | ||||||||||
| A3 | ||||||||||
Решение
Проверяем условие Данцига: 7 = 5 + 3 – 1.
Строим систему потенциалов. Задаем первой строке потенциал равный 100.
| Пункты отправления, A i | Пункты назначения Bj | Потенциалы | |||||||||
| B1 | B2 | B3 | B4 | Bф | |||||||
| A1 | |||||||||||
| A2 | |||||||||||
| A3 | |||||||||||
| Потенциалы |
Через заполненные клетки определяем потенциалы первого, второго, и третьего столбцов. Далее через клетку (A2,B3) определяем потенциал второй строки, через клетку (A2,B4) определяем потенциал четвертого столбца. После чего через клетку (A3,B4) определяем потенциал третей строки и через клетку (A3,Bф) потенциал последнего столбца.
Проверяем условие оптимальности. Оно не выполнено в клетках (A1,B4), где нарушение составляет 4, (A1,Bф), где нарушение составляет 4, (A2,B1), где нарушение составляет 6, (A2,B2), где нарушение составляет 6, (A2,Bф), где нарушение составляет 7 и (A3,B2), в которой нарушение составляет 2.
Применим формальное правило улучшение плана для клетки (A2,Bф), т.к. в ней выявлено наибольшее нарушение.

Получили следующий вид транспортной матрицы:
| Пункты отправления, A i | Пункты назначения Bj | |||||||||
| B1 | B2 | B3 | B4 | Bф | ||||||
| A1 | ||||||||||
| A2 | ||||||||||
| A3 | ||||||||||
Проверяем условие Данцига и строим систему потенциалов. Задаем первой строке потенциал, равный 100.
| Пункты отправления, A i | Пункты назначения Bj | Потенциалы | |||||||||
| B1 | B2 | B3 | B4 | Bф | |||||||
| A1 | |||||||||||
| A2 | |||||||||||
| A3 | |||||||||||
| Потенциалы |
Проверяем условие оптимальности. Оно не выполнено в клетках (A1,B4), где нарушение составляет 4, (A2,B1), где нарушение составляет 6, (A2,B2), где нарушение составляет 6 и (A3,B2), в которой нарушение составляет 2.
Применим формальное правило улучшения плана для клетки (A2,B1), т.к. в ней выявлено наибольшее нарушение.

Получили следующий вид транспортной матрицы:
| Пункты отправления, A i | Пункты назначения B j | |||||||||
| B1 | B2 | B3 | B4 | Bф | ||||||
| A1 | ||||||||||
| A2 | ||||||||||
| A3 | ||||||||||
Проверяем условие Данцига и строим систему потенциалов. Задаем второй строке потенциал равный 100.
| Пункты отправления, A i | Пункты назначения B j | Потенциалы | |||||||||
| B1 | B2 | B3 | B4 | Bф | |||||||
| A1 | |||||||||||
| A2 | |||||||||||
| A3 | |||||||||||
| Потенциалы |
Проверяем условие оптимальности. Оно не выполнено в клетках (A1,B4), где нарушение составляет 4, (A2,B2), где нарушение составляет 6 и (A3,B2), в которой нарушение составляет 2.
Применим формальное правило улучшение плана для клетки (A2,B2), т.к. в ней выявлено наибольшее нарушение.
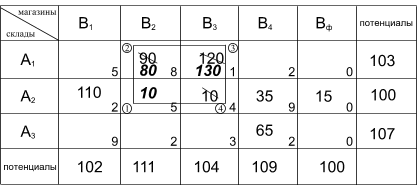
Получили следующий вид транспортной матрицы:
| Пункты отправления, Ai | Пункты назначения Bj | |||||||||
| B1 | B2 | B3 | B4 | Bф | ||||||
| A1 | ||||||||||
| A2 | ||||||||||
| A3 | ||||||||||
Проверяем условие Данцига и строим систему потенциалов. Задаем второй строке потенциал равный 100.
| Пункты отправления, A i | Пункты назначения B j | Потенциалы | |||||||||
| B1 | B2 | B3 | B4 | Bф | |||||||
| A1 | |||||||||||
| A2 | |||||||||||
| A3 | |||||||||||
| Потенциалы |
Проверяем условие оптимальности. Оно не выполнено в клетке (A1,B4), где нарушение составляет 4.
Применим формальное правило улучшения плана для клетки (A1,B4).
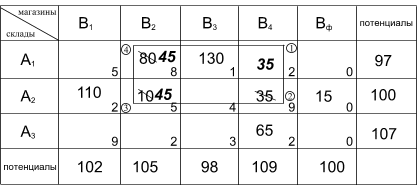
Получили следующий вид транспортной матрицы:
| Пункты отправления, A i | Пункты назначения B j | |||||||||
| B1 | B2 | B3 | B4 | Bф | ||||||
| A1 | ||||||||||
| A2 | ||||||||||
| A3 | ||||||||||
Проверяем условие Данцига и строим систему потенциалов. Задаем второй строке потенциал равный 100.
| Пункты отправления, A i | Пункты назначения B j | Потенциалы | |||||||||
| B1 | B2 | B3 | B4 | Bф | |||||||
| A1 | |||||||||||
| A2 | |||||||||||
| A3 | |||||||||||
| Потенциалы |
Проверяем условие оптимальности. Оно не выполнено в клетках (A1,Bф), где нарушение составляет 2, (A3,B2), где нарушение составляет 5 и (A3,Bф), в которой нарушение составляет 2.
Применим формальное правило улучшение плана для клетки (A3,B2), т.к. в ней выявлено наибольшее нарушение.
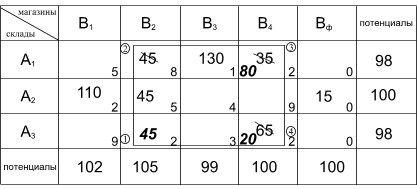
Получили следующий вид транспортной матрицы:
| Пункты отправления, A i | Пункты назначения B j | |||||||||
| B1 | B2 | B3 | B4 | Bф | ||||||
| A1 | ||||||||||
| A2 | ||||||||||
| A3 | ||||||||||
Проверяем условие Данцига и строим систему потенциалов. Задаем второй строке потенциал равный 100.
| Пункты отправления, A i | Пункты назначения B j | Потенциалы | |||||||||
| B1 | B2 | B3 | B4 | Bф | |||||||
| A1 | |||||||||||
| A2 | |||||||||||
| A3 | |||||||||||
| Потенциалы |
Проверяем условие оптимальности. Оно выполнено во всех клетках, следовательно получен оптимальный план перевозок. Суммарные затраты за транспортировку составит:
 .
.
Отметим, что мы за нулевое приближение; мы выбрали опорный план, полученный методом «северо-западного угла», в силу чего нам и пришлось производить большое количество итераций. Если бы в качестве начального приближения был выбран опорный план, полученный методом «минимального элемента», то необходимое количество итераций было бы существенно меньше, а при выборе в качестве исходного опорного плана построенного «методом Фогеля», в данном примере вообще не пришлось бы производить итерации.
Отметим также, что при решении данного примера контуры которые мы строили, получались прямоугольные; это не всегда так, контуры могут быть различных форм, но строятся они всегда по одному принципу и в каждом случае могут быть получены единственным образом.

Задание № 1
Предприятие выпускает два вида продукции, для производства каждого из которых используется сырьё двух типов. На изготовление тысячи единиц изделия первого вида требуется затратить сырья каждого типа 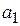 и
и  тонн соответственно, а для тысячи единиц изделия второго вида
тонн соответственно, а для тысячи единиц изделия второго вида  и
и  тонн соответственно. Согласно заключенным договорам поставки сырья первого типа не должны превышать
тонн соответственно. Согласно заключенным договорам поставки сырья первого типа не должны превышать 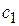 тонн, а поставки сырья второго типа не могут быть снижены, менее чем до
тонн, а поставки сырья второго типа не могут быть снижены, менее чем до  тонн. Причем суммарный выпуск продукции должен находиться в следующем диапазоне: увеличенное в
тонн. Причем суммарный выпуск продукции должен находиться в следующем диапазоне: увеличенное в  раз количество продукции второго вида не может превышать более чем на
раз количество продукции второго вида не может превышать более чем на 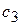 тысяч единиц количество продукции первого вида, увеличенное в
тысяч единиц количество продукции первого вида, увеличенное в  раз; а в свою очередь увеличенное в
раз; а в свою очередь увеличенное в  раз количество продукции первого вида не может превышать более чем на
раз количество продукции первого вида не может превышать более чем на  тысяч единиц количество продукции второго вида, увеличенное в
тысяч единиц количество продукции второго вида, увеличенное в  раз.
раз.
Стоимость тысячи единиц изделий первого вида составляет  тыс. руб., а тысячи единиц изделия второго вида
тыс. руб., а тысячи единиц изделия второго вида 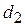 тыс. руб.
тыс. руб.
Требуется составить план производства изделий, обеспечивающий максимальную прибыль предприятию:
а) решите задачу графическим методом;
б) решите задачу симплекс-методом.
Данные к задаче по вариантам приведены в таблице 1:
Задание № 2
На трех складах находятся запасы продукции в количестве а 1, а 2, а 3, единиц соответственно, а в четырех магазинах имеется необходимость в завозе данной продукции, причем потребности составляют b 1, b 2, b 3, b 4.едениц продукции соответственно, тарифы на транспортировку продукции с i -того склада к j -тому магазину равны сi,j. Необходимо построить оптимальный план перевозок и определить минимальные затраты на транспортировку.
Данные к задаче по вариантам приведены в таблице 2:
Таблица 1
| вариант | 
| 
| 
| 
| 
| 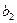
| 
| 
| 
| 
| 
| 
| 
| 
|
Таблица 2
| Вар. | 
| 
| 
| 
| 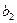
| 
| 
| 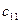
| 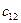
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
|
ЛИТЕРАТУРА
1. Тернер Д. Вероятность, статистика и исследование операций./ Тернер Д. - М.: Статистика,1976.
2. Экономико-математические методы и прикладные модели. /Под ред. В.В. Федосеева. - М.: ЮНИТИ, 1999.
3. Акулич И.Л. Математическое программирование в примерах и задачах./ Акулич И.Л. - М.: Высшая школа,1993.
4. Расс С. Линейное программирование (методы и приложения). / Расс С. - М.: Физматгиз, 1961.
5. Архипенков С.М. Экономико-математические модели формирования оптимальных (напряженных) и надежных планов производства на предприятиях обрабатывающей промышленности. / Архипенков С.М. - Тамбов: Изд-во Тамб. гос. тех. уп-т. 1999.
6. Коссов В.В. Межотраслевые модели. / Коссов В.В. - М.: Экономика, 1973.
7. Кремер Н.Ш., Тришин И.М., Фридман М.Н. Исследование операций в экономике: Учеб. пособие для вузов. /Н.Ш. Кремера. - М.: ЮНИТИ, 1997.
8. Шелобаев С.И. Математические методы и модели в экономике, финансах и бизнесе: Учебник для вузов. / Шелобаев С.И. - М.: ЮНИТИ, 2000.
9. Грешилов А.Н. Использование MS Excel и VBA в экономике и финансах./ Грешилов А.Н. –СПб.:; БВХ. – 2000.
Содержание
ПРЕДИСЛОВИЕ 3
Раздел 1. Линейное программирование 4
1.1 Графический метод решения задач ЛП 11
1.2 Симплекс метод решения задач ЛП 16
Раздел 2. Транспортная задача 18
ЛИТЕРАТУРА 38
Учебное издание
МАТЕМАТИЧЕСКИЕ МЕТОДЫ В ЭКОНОМИКЕ
Date: 2016-07-25; view: 452; Нарушение авторских прав