Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Раздел 1. Линейное программирование
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Государственное образовательное учреждение
Высшего профессионального образования
КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ
ЭНЕРГЕТИЧЕСКИЙ УНИВЕРСИТЕТ»
МАТЕМАТИЧЕСКИЕ МЕТОДЫ В ЭКОНОМИКЕ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Для подготовки к практическим занятиям по дисциплине
«Экономико-математическое моделирование»
Казань 2012
УДК
ББК
М34
М34 Математические методы в экономике: Методические указания для подготовки к практическим занятиям по дисциплине «Экономико-математическое моделирование», авторы: С.А. Лившиц, Р.Ф. Ахвердиев, М.Г. Лившиц / Казань: Казан. гос. энерг. ун-т, 2012, -38.
Представлены методические указания для выполнения практических занятий по дисциплине «Экономико-математическое моделирование». Предназначены для студентов специальности 08052.65 «Экономика и управления на предприятии (энергетика)», направления подготовки 080100 «Экономика»
УДК
ББК
ã Казанский государственный энергетический университет, 2012.
ПРЕДИСЛОВИЕ
Методические указания предназначены для оказания помощи студентам при решении задач на практических занятиях по дисциплине «Экономико-математическое моделирование».
Дисциплина «Экономико-математическое моделирование» является одной из основных при подготовке дипломированных специалистов – экономистов. Студенты, изучившие данную дисциплину, должны ориентироваться в основных, применяемых в настоящее время, моделях, используемых для анализа, и активно использовать полученные знания для решения научных и практических задач.
В данном пособии мы рассмотрим наиболее простые и хорошо алгоритмизируемые разделы экономико-математического моделирования, такие как линейное программирование и модели оптимизации производственных планов.
Раздел 1. ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
Во многих ситуациях, встречающихся в промышленности, сельском хозяйстве, экономической деятельности и т.д., задача оптимизации плана некоторых экономико-производственных действий может быть записана в виде линейных уравнений и неравенств с линейным же, относительно искомых, определяющих этот план, переменных целевой функцией. К задачам этого же вида сводятся очень многие задачи оптимизации и принятия решений из некоторых других самостоятельных направлений прикладной математики.
Соответственно возникает потребность в математической теории, позволяющей решать такие задачи. Такая теория существует и называется линейным программированием. Данное название возникло в 30-е годы, когда представления о программировании на компьютере ещё не существовало. Под программированием фактически подразумевается планирование. Однако, этот термин уже укоренился, и не только в линейном случае. Имеются так же и такие названия математических теорий решения задач оптимизации, как нелинейное программирование и динамическое программирование.
В общем виде задача линейного программирования (ЛП) заключается в отыскании таких неотрицательных чисел x 1, x 2..., х nкоторые максимизируют (минимизируют) линейную функцию:
при условии выполнения системы неравенств :
При описании реальной ситуации с помощью линейной модели следует проверять наличие у модели таких свойств, как пропорциональность и аддитивность. Пропорциональность означает, что вклад каждой переменной в целевую функцию (ЦФ) и общий объем потребления соответствующих ресурсов должен быть прямо пропорционален величине этой переменной. Например, если продавая какой либо товар в общем случае по одной цене рублей, фирма будет делать скидку при определенном уровне закупки, то будет отсутствовать прямая пропорциональность между доходом фирмы и величиной переменной. Т.е. в разных ситуациях одна единица товара будет приносить разный доход. Аддитивность означает, что ЦФ и ограничения должны представлять собой сумму вкладов от различных переменных. Примером нарушения аддитивности служит ситуация, когда увеличение сбыта одного из конкурирующих видов продукции, производимых одной фирмой, влияет на объем реализации другого.
При решении задачи линейного программирования целесообразно бывает введение следующих определений.
Допустимое решение – это совокупность чисел (план) 
, удовлетворяющих ограничениям исходной задачи.
Оптимальное решение – это план, при котором ЦФ принимает свое максимальное (минимальное) значение.
Прежде чем построить математическую модель задачи, т.е. записать ее с помощью математических соотношений, необходимо четко разобраться с экономической ситуацией, описанной в условии. Для этого необходимо с точки зрения экономики, а не математики, ответить на следующие вопросы:
1) Что является искомыми величинами задачи?
2) Какой параметр задачи служит критерием эффективности (оптимальности) решения? (это может быть: прибыль, время, количество отходов и т.д.)
3) В каком направлении должно изменяться значение этого параметра (к max или к min) для достижения наилучших результатов?
4) Какие условия в отношении искомых величин и ресурсов задачи должны быть выполнены? Эти условия устанавливают, как должны соотноситься друг с другом различные параметры задачи, например, количество ресурса, затраченного при производстве, и его запас на складе; количество выпускаемой продукции и емкость склада, где она будет храниться; количество выпускаемой продукции и рыночный спрос на эту продукцию и т.д.
Только после экономического ответа на все эти вопросы можно приступать к записи этих ответов в математическом виде, т.е. к записи математической модели.
а) Искомые величины являются переменными задачи, которые как правило обозначаются малыми латинскими буквами с индексами, например, однотипные переменные удобно представлять в виде .
б) Цель решения записывается в виде целевой функции, обозначаемой, например, 
. Математическая формула ЦФ отражает способ расчета значений параметра – критерия эффективности задачи.
в) Условия, налагаемые на переменные и ресурсы задачи, записываются в виде системы равенств или неравенств, т.е. ограничений. Левые и правые части ограничений отражают способ получения (расчет или численные значения из условия задачи) значений тех параметров задачи, на которые были наложены соответствующие условия.
В процессе записи математической модели целесообразно указывать единицы измерения переменных задачи, целевой функции и всех ограничений.
Задача
Фабрика производит два вида красок: первый – для наружных, а второй – для внутренних работ. Для производства красок используются два ингредиента: А и В. Известны расходы ингредиентов А и В на 1 т соответствующих красок и максимально возможные суточные запасы этих ингредиентов на складе. Данные по расходам ингредиентов на краски первого и второго вида представлены в таблице.
| Ингредиенты | Расход ингредиентов, т ингр./т краски | Запас, т ингр./сутки | |
| Краска 1-го вида | Краска 2-го вида | ||
| А | |||
| В |
Изучение рынка сбыта показало, что суточный спрос на краску 2-го вида никогда не превышает спроса на краску 1-го вида более, чем на 1 т. Кроме того, установлено, что спрос на краску 2-го вида никогда не превышает 2 т в сутки. Оптовые цены одной тонны красок равны: 3 тыс. руб. для краски 1-го вида; 2 тыс. руб. для краски 2-го вида.
Необходимо построить математическую модель, позволяющую установить, какое количество краски каждого вида надо производить, чтобы доход от реализации продукции был максимальным.
Решение
В задаче требуется установить, сколько краски каждого вида надо производить. Поэтому искомыми величинами, а значит, и переменными задачи являются суточные объемы производства каждого вида красок:
– суточный объем производства краски 1-го вида, [т краски/сутки];
– суточный объем производства краски 2-го вида, [т краски/сутки].
В условии задачи сформулирована цель – добиться максимального дохода от реализации продукции. Т.е. критерием эффективности служит параметр суточного дохода, который должен стремиться к максимуму. Чтобы рассчитать величину суточного дохода от продажи красок обоих видов, необходимо знать объемы производства красок, т.е. и т краски в сутки, а также оптовые цены на краски 1-го и 2-го видов – согласно условию, соответственно 3 и 2 тыс. руб. за 1 т краски. Таким образом, доход от продажи суточного объема производства краски 1-го вида равен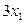 
тыс. руб. в сутки, а от продажи краски 2-го вида – 
тыс. руб. в сутки. Поэтому запишем ЦФ в виде суммы дохода от продажи красок 1-го и 2-го видов (при допущении независимости объемов сбыта каждой из красок)
[тыс. руб./сутки],
.
Возможные объемы производства красок и ограничиваются следующими условиями:
· количество ингредиентов А и В, израсходованное в течение суток на производство красок обоих видов, не может превышать суточного запаса этих ингредиентов на складе;
· согласно результатам изучения рыночного спроса суточный объем производства краски 2-го вида может превышать объем производства краски 1-го вида, но не более, чем на 1 т краски;
· объем производства краски 2-го вида не должен превышать 2 т в сутки, что также следует из результатов изучения рынков сбыта;
· объемы производства красок не могут быть отрицательными.
Таким образом, все ограничения задачи делятся на 3 группы, обусловленные:
1) расходом ингредиентов;
2) рыночным спросом на краску;
3) неотрицательностью объемов производства.
Ограничения по расходу любого из ингредиентов имеют следующую содержательную форму записи:
.
Запишем эти ограничения в математической форме.
Левая часть ограничения – это формула расчета суточного расхода конкретного ингредиента на производство красок. Так из условия известен расход ингредиента А на производство 1 т краски 1-го вида (1 т ингр. А) и 1 т краски 2-го вида (2 т ингр. А). Тогда на производство 
т краски 1-го вида и т краски 2-го вида потребуется 
т ингр. А.
Правая часть ограничения – это величина суточного запаса ингредиента на складе, например, 6 т ингредиента А в сутки. Таким образом, ограничение по расходу А имеет вид
.
Аналогична математическая запись ограничения по расходу В
.
Примечание. Следует всегда проверять размерность левой и правой частей каждого из ограничений, поскольку их несовпадение свидетельствует о принципиальной ошибке при составлении ограничений.
Ограничение по суточному объему производства краски 1-го вида по сравнению с объемом производства краски 2-го вида имеет
содержательную форму
и математическую форму
.
Ограничение по суточному объему производства краски 1-го вида имеет
содержательную форму
и математическую форму
.
Неотрицательность объемов производства задается как
.
Таким образом, математическая модель этой задачи имеет вид
Для задач линейного программирования, содержащих только две переменные 
и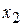 
применим графический способ решения. Этот способ основан на том факте, что в случае двух переменных множество допустимых решений можно построить на двухмерной плоскости.
Date: 2016-07-25; view: 357; Нарушение авторских прав