Методика решения задач ЛП графическим методом

I. В ограничениях задачи замените знаки неравенств на знаки точных равенств и постройте соответствующие прямые.

II. Найдите и заштрихуйте полуплоскости, разрешенные каждым из ограничений-неравенств задачи. Для этого подставьте в конкретное неравенство координаты какой-либо точки [например, (0;0)], и проверьте истинность полученного неравенства.

Если неравенство истинное, то надо заштриховать полуплоскость, содержащую данную точку; иначе (неравенство ложное) надо заштриховать полуплоскость, не содержащую данную точку.

Поскольку x ₁ и x ₂ должны быть неотрицательными, то их допустимые значения всегда будут находиться выше оси Оx₁ и правее оси О x ₂, т.е. в I-м квадранте. Ограничения-равенства разрешают только те точки, которые лежат на соответствующей прямой, поэтому выделите на графике такие прямые.

III. Определите ОДР как часть плоскости, принадлежащую одновременно всем разрешенным областям, и выделите ее. При отсутствии ОДР задача не имеет решений, о чем сделайте соответствующий вывод.

IV. Если ОДР – не пустое множество, то определите координаты угловых точек. Определение координат сводится к решению системы соответствующих линейных уравнений.

V. Подставьте координаты угловых точек в уравнение для ЦФ и найдите max (min) значение целевой функции.

Можно вместо перебора всех угловых точек (пункт IV, V ) произвести следующие действия:

IV.а Провести вектор, координатами которого служат коэффициенты в уравнении с целевой функцией. Сдвигать прямую перпендикулярную построенному вектору от начала по направлению вектора до момента, когда пересечение сдвигаемой прямой с ОДР будет составлять одну точку.

V.а Координаты найденной точки будут являться оптимальным планом, а если их подставить в уравнение целевой функции, то получим ее max (min) значение.

Задача

Найдем оптимальное решение задачи о красках, математическая модель которой имеет вид:

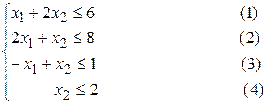
Построим прямые ограничений (рис. 1).

Рис. 1. Графическое решение задачи

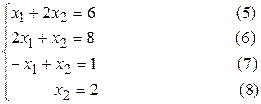
Определим ОДР. Например, подставим точку (0;0) в исходное ограничение (3), получим 0 ≤ 1, что является истинным неравенством, поэтому стрелкой (или штрихованием) обозначим полуплоскость, содержащую точку (0;0), т.е. расположенную правее и ниже прямой (3). Аналогично определим допустимые полуплоскости для остальных ограничений и укажем их стрелками у соответствующих прямых ограничений (см. рис. 1). Общей областью, разрешенной всеми ограничениями, т.е. ОДР является многоугольник ABCDEF.

Найдем координаты точек пересечения прямых ограничений, т.е. координаты угловых точек. В некоторых случаях хороший рисунок позволяет сразу определять координаты угловых точек.

;

;

;

;

Для определения координаты точки Е решим систему уравнений с ограничениями (5) и (6).

Решая данную систему получаем:

.

Найдем значение целевой функции в угловых точках, т.е. подставим их координаты в уравнение .

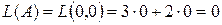
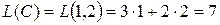
Е – это точка максимума ЦФ.

Таким образом, наилучшим режимом работы фирмы является ежесуточное производство краски 1-го вида в объеме 3 1/3 т и краски 2-го вида в объеме 1 1/3 т. Доход от продажи красок составит 12 2/3 тыс. руб. в сутки.

Решая графическим методом, предполагающим построение целевого вектора, проводим вектор, координатами которого служат коэффициенты в уравнении с целевой функцией ; сдвигая прямую, перпендикулярную построенному вектору (от начала к концу), найдем точку, являющуюся последней в пересечении сдвигаемой прямой с ОДР (это точка Е), ее координаты, найденные из решения системы соответствующих уравнений, будут являться оптимальным планом, а значение целевой функции в ней будет max.

В более общем случае разработан и широко применяется универсальный метод решения любой задачи ЛП, называемый симплекс-методом.

Симплекс – метод, как метод решения задач ЛП был предложен американским математиком-экономистом Данцигом в 1951 году.

Графически симплекс метод представляет из себя передвижение по выпуклому многограннику от вершины к вершине, при этом значение целевой функции на каждом шаге улучшается до тех пор, пока не достигается оптимум.

Идея симплекс – метода состоит в том, чтобы преобразовать уравнение содержащее целевую функцию к виду: , т.к. в этом случае становиться возможным выразить , а в силу того что перед нами ставится задача максимизировать L, то эта задача достигается в случае, когда все переменные, присутствующие в данном уравнении, принимают нулевые значения (т.к. переменные не отрицательны по условию).

Date: 2016-07-25; view: 300; Нарушение авторских прав