
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Двойное лучепреломление
|
|
Эллиптическая поляризация – наиболее общий случай поляризации световых волн, она возникает при сложении двух когерентных взаимно перпендикулярных колебаний различной амплитуды.
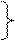

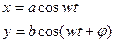


(1)
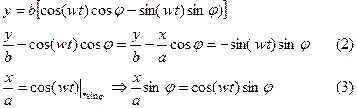

 (4) возведем в квадрат и сложим
(4) возведем в квадрат и сложим
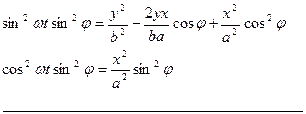
+

y b
 уравнение эллипса (5) a x
уравнение эллипса (5) a x
 При φ=0 эллипс вырождается в линию, т.е. колебания синфазные:
При φ=0 эллипс вырождается в линию, т.е. колебания синфазные:
 y
y
(7) (6)
x
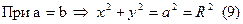 Уравнение круга; конец вектора с составляющими x и y описывает окружность.
Уравнение круга; конец вектора с составляющими x и y описывает окружность.
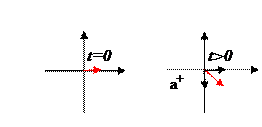 Если φ = π/2 из уравнения (1)
Если φ = π/2 из уравнения (1)  то колебания по x отстают по фазе от колебаний по y на π/2, в момент t=0 конец вектора лежит на оси x в точке x = a, а y -ой компоненты нет. (Рис. 1)
то колебания по x отстают по фазе от колебаний по y на π/2, в момент t=0 конец вектора лежит на оси x в точке x = a, а y -ой компоненты нет. (Рис. 1)
В последующие моменты (t>0) x -ая компонента уменьшается, а y -ая компонента растет в отрицательном направлении, поскольку к
аргументу φ = π/2 добавляется ωt. (Рис. 2)
Рис.1 Рис. 2
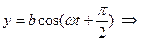
 происходит вращение по часовой стрелке. Такое вращение называется «правое вращение» и, наоборот, против часовой стрелке – «левое вращение».
происходит вращение по часовой стрелке. Такое вращение называется «правое вращение» и, наоборот, против часовой стрелке – «левое вращение».
И так, если волна распространяется к смотрящему на чертёж, Рис. 2, с вектором 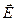 вращающимся по часовой стрелке, то говорят о волне с правой поляризацией по кругу, в противном случае – с левой поляризацией по кругу (a-).
вращающимся по часовой стрелке, то говорят о волне с правой поляризацией по кругу, в противном случае – с левой поляризацией по кругу (a-).
Если рассмотреть сумму,  то их сумма направлена вдоль оси Oy, тогда получаем линейно-поляризованную волну. В каждый момент t они занимают симметричные относительно оси y положения, и их сложение
то их сумма направлена вдоль оси Oy, тогда получаем линейно-поляризованную волну. В каждый момент t они занимают симметричные относительно оси y положения, и их сложение 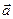 всегда направлено по оси y, это линейно-поляризованное колебание. Тогда линейно-поляризованная волна представляет собой сумму двух волн с круговой поляризацией, одна – правая, другая имеет левую поляризацию.
всегда направлено по оси y, это линейно-поляризованное колебание. Тогда линейно-поляризованная волна представляет собой сумму двух волн с круговой поляризацией, одна – правая, другая имеет левую поляризацию.
Двойное лучепреломление
В природе существуют вещества, в которых скорости распространения а+ и а- различны, следовательно, будут различны и n+ и n-, и если будет распространяться линейно-поляризованная волна, то возникает её разделение на две волны, которые выходят под различными углами  двойное лучепреломление. Это имеет место для поперечных электромагнитных волн в ионизированном газе или в фирите в магнитном поле. Существуют также кристаллы, в которых свет испытывает двойное лучепреломление, это исландский шпат (CaCO3 - разновидность углекислого кальция), в природе их довольно много, они оптически чистые и бывают больших размеров.
двойное лучепреломление. Это имеет место для поперечных электромагнитных волн в ионизированном газе или в фирите в магнитном поле. Существуют также кристаллы, в которых свет испытывает двойное лучепреломление, это исландский шпат (CaCO3 - разновидность углекислого кальция), в природе их довольно много, они оптически чистые и бывают больших размеров.

Рис. 4. Кристалл исландского шпата в виде ромбоэдра.
 Первоначальный пучок перпендикулярный к грани φi. Пучок делится на два, причем один из них является продолжением первичного = обыкновенная волна (О”), а второй уклоняется так, что угол преломления отличается от нулевого, (Е”) - необыкновенная волна.
Первоначальный пучок перпендикулярный к грани φi. Пучок делится на два, причем один из них является продолжением первичного = обыкновенная волна (О”), а второй уклоняется так, что угол преломления отличается от нулевого, (Е”) - необыкновенная волна.
Рис. 5
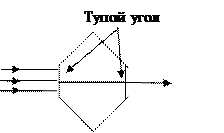
При распространении вдоль оптической оси кристалла, двойное лучепреломление отсутствует.
Это явление было открыто Бартолином в 1670г., Гюйгенс 1690г. и для УКВ - диапазона, Лебедевым в ХХ веке.
Рис. 6
Для необыкновенного луча показатель преломления ne зависит от направления луча в кристалле, для nо – остается постоянным при любом угле падения светового луч в кристалл.
Для исландского шпата:
λ = 5893Ǻ (желтый дублет натрия)
nо = 1,658 а 1,486≤ ne 1,658
ne ≤ nо  так называемые отрицательные кристаллы.
так называемые отрицательные кристаллы.
Существуют кристаллы с ne ≥ nо – положительные кристаллы, кристаллический кварц. При ne = nо  ось кристалла (оптическая ось).
ось кристалла (оптическая ось).
Любая плоскость, приведенная через оптическую ось, называется главным сечением. В природе существуют одноосные и двухосные кристаллы.
Одноосные кристаллы: исландский шпат и кварц.
Оба луча, возникающие в кристалле при двойном лучепреломлении, полностью поляризованы в двух взаимно перпендикулярных плоскостях.
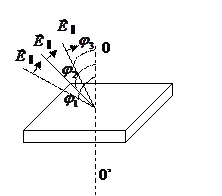
 Главным сечением считают плоскость, проходящую через падающий на кристалл луч и направление оптической оси.
Главным сечением считают плоскость, проходящую через падающий на кристалл луч и направление оптической оси.
Рис. 7
(a) (b)
Вектор 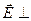 главному сечению Вектор
главному сечению Вектор 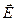 ║ главному сечению
║ главному сечению
Рассмотрим два случая ориентации вектора 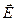 (
( и
и 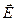 ║) относительно главного сечения: Если
║) относительно главного сечения: Если 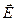 перпендикулярно главному сечению, то изменение угла падения φ не изменяет взаимную ориентацию
перпендикулярно главному сечению, то изменение угла падения φ не изменяет взаимную ориентацию 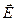 и оптическая ось ОО’ (рис. 7а.). Для
и оптическая ось ОО’ (рис. 7а.). Для 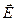 ║ главной плоскости сечения, при изменении угла падения меняется угол между оптической осью и направлением вектора
║ главной плоскости сечения, при изменении угла падения меняется угол между оптической осью и направлением вектора 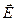 . Это приводит к зависимости показателя преломления от угла падения. Такие кристаллы называют анизотропные.
. Это приводит к зависимости показателя преломления от угла падения. Такие кристаллы называют анизотропные.
В случае произвольной ориентированной линейной поляризации луча, падающего на кристалл можно разложить на 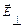 и
и  ║ относительно сечения ОО’, тогда
║ относительно сечения ОО’, тогда 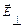 не испытывает зависимости от φ i – угла падения, и для нее n = const
не испытывает зависимости от φ i – угла падения, и для нее n = const  no, т.е. обыкновенный луч. Вторая компонента,
no, т.е. обыкновенный луч. Вторая компонента, 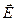 ║, распространения в кристалле с другой скоростью, т.к. n = n(φi)
║, распространения в кристалле с другой скоростью, т.к. n = n(φi)  ne. Таким образом, луч разделяется на два луча, no и ne.
ne. Таким образом, луч разделяется на два луча, no и ne.
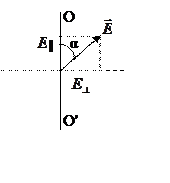
Если введем угол α между 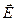 и ОО’, то получим
и ОО’, то получим

 Через каждые π/2 или I0 или Ie обращаются в нуль.
Через каждые π/2 или I0 или Ie обращаются в нуль.
Из правила Малю следует, что при падении на анизотропный кристалл неполяризованного света происходит его разделение на две компоненты (обыкновенную и необыкновенную), которые линейно поляризованы. Вследствие разной величины no и ne идут по разным путям и выходят из кристалла в виде двух линейно поляризованных лучей.
Следовательно, анизотропный кристалл служит поляризатором света.
Поляризационные приспособления
Для х-ки поляризации света вводится так называемая степень поляризации P:

Пластинки из анизотропных кристаллов и их комбинаций применяются для получения поляризованного света.
- Призма Николя (Николь). Исландский шпат.

В
С’ А о
е
Рис. 10
По линии АА призма разрезается и склеивается канадским бальзамом с пδ =1,550, пе<пδ<пο. Оптическая ось составляет со входной гранью угол в 48 градусов. Можно подобрать угол, при котором существует полное внутреннее отражение на прослойке канадского бальзама и поглощается зачерненной нижней гранью (для больших призм ставят дополнительную призму для вывода луча, чтобы избежать её нагрева).
Необыкновенный луч ne выходит параллельный грани АС’. Но так как канадский бальзам поглощает ультрафиолетовое излучение, и в качестве поляризаторов в УФ используют призму Волластона, из исландского шпата, с воздушной (или глицериновой) прослойкой.
С глицерином
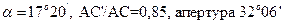 при которой еще можно получить поляризацию.
при которой еще можно получить поляризацию.
С воздушной прослойкой
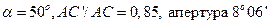 она пригодна для ультрафиолета.
она пригодна для ультрафиолета.
2. Двояко преломляющие призмы
 а)
а)
шпат О Луч О преломляется в шпате и стекло раза в два и сильно
отклоняется. Луч Е выходит почти без отклонения, так как nстекла близкий к ne:
е

Стекло
Рис. 11
б) Призма из двух кусков исландского шпата с различными направлениями оптических лучей. Различие в ориентации оптических осей влияет на угол расхождения между лучами. Допустимая апертура падающего пучка во всех этих призмах весьма не велика.
3. ---------------------- пластинки (турмалин). Наряду с двойным лучепреломлением
существует поглощение, сильнее необыкновенного луча, чем “О” луча. Из пластинки оба луча выходят поляризованными во взаимно перпендикулярных плоскостях. При толщине 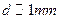 , обыкновенный луч целиком поглощается и вышедший луч будет плоскополяризованным, следовательно, существуют некоторые участки видимого света где необыкновенный луч испытывает частичное поглощение,
, обыкновенный луч целиком поглощается и вышедший луч будет плоскополяризованным, следовательно, существуют некоторые участки видимого света где необыкновенный луч испытывает частичное поглощение,  еще оказывается окрашенной
еще оказывается окрашенной  турмалин является поляризатором и еще светофильтром, практически пропускающим желто-зеленую область видимого спектра. Дихроизм (плеохроизм = многоцветность) – это явление, когда поглощение зависит от λ и, следовательно, по разным направлениям разная окраска.
турмалин является поляризатором и еще светофильтром, практически пропускающим желто-зеленую область видимого спектра. Дихроизм (плеохроизм = многоцветность) – это явление, когда поглощение зависит от λ и, следовательно, по разным направлениям разная окраска.
Лекция
Дисперсия (приборов)
Основные свойства спектральных приборов
В экспериментах по получению спектров обычно используют призму или дифракционную решетку, призмы и дифракционные решетки играют основную роль при создании спектральных приборов. Эти диспергирующие элементы обеспечивают разложение по длинам волн. Кроме них спектральный прибор должен содержать какую-то фокусирующую оптику, чтобы получить четкое изображение входной щели в свете исследуемой волны ( ) (спектральную линию) этот прибор называется спектрографом. Излучение определенного интервала длин волн можно вывести через выходную щель. Так работают монохроматор
) (спектральную линию) этот прибор называется спектрографом. Излучение определенного интервала длин волн можно вывести через выходную щель. Так работают монохроматор
.
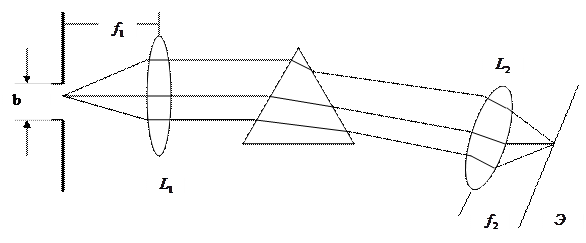
рис 1. упрощенная схема спектрального прибора
Простейшая схема спектрального прибора: в главном фокусе колец–мажорного объектива L1 помещена входная щель b. При прохождении излучения через такую систему образуется плоская волна, падающая на дисперцирующий элемент. Второй (камерный) объектив L2 фокусирует излучение разных длин волн (спектральных линий) в определенных точках фотопластинки. Подобная система отнюдь не является единственно возможном (например, интерференционный фильтр позволяет выделить из исследуемого спектра узкую группу волн, и также служит монохроматором).
Прежде чем проводить анализ полученных спектральных линий следует ответить на следующие принципиальные вопросы:
- является ли разложение произвольного излучения по длинам волн единственным?
- в какой степени свойства спектрального прибора могут влиять на характер получаемого спектра?
- Согласно теореме Фурье, любую функцию F(t) можно заменить конечной или бесконечной суммой гармонических функций вида:
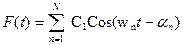 (1)
(1)
 (2)
(2)
Из (2) следует, если известны амплитуды 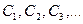 монохроматических колебаний с частотами
монохроматических колебаний с частотами 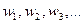 то сложив квадраты амплитуд найдем среднее значение функции
то сложив квадраты амплитуд найдем среднее значение функции  .
.
|

Для сопоставления экспериментального (физического) и математического разложения функция F(t) на составляющие, рассмотрим случай, когда F(t) состоит из трех монохроматических функций с частотами 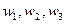 тогда
тогда
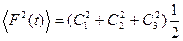
Затем настроим монохроматор поочередно на 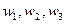 неизбежное искажение сигнала, вносимое всеми составными частотами спектрального прибора, характеризуется аппаратной функцией, которая показывает, каков результат измерения частоты монохроматического излучения, которого на вход спектрального прибора.
неизбежное искажение сигнала, вносимое всеми составными частотами спектрального прибора, характеризуется аппаратной функцией, которая показывает, каков результат измерения частоты монохроматического излучения, которого на вход спектрального прибора.
Будем считать, что разность между  и
и 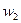 ,
, 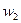 и
и 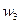 ,
, 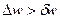 значительно превышает ширину аппаратной функции, чтобы измерение на одной частоте не привела к искажению измерений на другой частоте и мы зарегистрируем три мах. Тогда отношение квадратов амплитуд (или отношение площадей под пиками) будет равно отношению
значительно превышает ширину аппаратной функции, чтобы измерение на одной частоте не привела к искажению измерений на другой частоте и мы зарегистрируем три мах. Тогда отношение квадратов амплитуд (или отношение площадей под пиками) будет равно отношению  и сумма площадей
и сумма площадей  определит среднее значение исследуемой функции. Следовательно спектральный прибор, выделив sin составляющие из исследуемого излучения,как бы провел экспериментальное разложение заданной функции в ряд Фурье.
определит среднее значение исследуемой функции. Следовательно спектральный прибор, выделив sin составляющие из исследуемого излучения,как бы провел экспериментальное разложение заданной функции в ряд Фурье.
Если функция произвольная, ее представляют в виде интеграла Фурье, а прибор (дает) регистрирует сплошной спектр. Построение 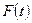 затруднено тем, что разложение позволяет лишь установить амплитуды гармонических колебаний, но не их начальные фазы. Так, например, нельзя утверждать, что белый свет возникает из семи цветов хотя разложение белого света в сплошной спектр дает семь цветов. Любой прибор не только выделяет периодические составляющие, но и как бы преобразует их, что можно описать при посредстве его аппаратной функции. Для математического описания такого преобразования обычно используют свертку, устанавливая связь между суммой произведений аппаратной функции на истинный контур линии и наблюдаемым на опыте распределением по частотам энергии светового потока в пределах исследуемой спектральной линии. В некоторых случаях удается исключить влияние прибора, т.е. выявить истинный контур спектральной линии (когда спектральный прибор, вообще говоря, не может разделить излучение на двух длинах волн, находящихся в пределах его аппаратной функции).
затруднено тем, что разложение позволяет лишь установить амплитуды гармонических колебаний, но не их начальные фазы. Так, например, нельзя утверждать, что белый свет возникает из семи цветов хотя разложение белого света в сплошной спектр дает семь цветов. Любой прибор не только выделяет периодические составляющие, но и как бы преобразует их, что можно описать при посредстве его аппаратной функции. Для математического описания такого преобразования обычно используют свертку, устанавливая связь между суммой произведений аппаратной функции на истинный контур линии и наблюдаемым на опыте распределением по частотам энергии светового потока в пределах исследуемой спектральной линии. В некоторых случаях удается исключить влияние прибора, т.е. выявить истинный контур спектральной линии (когда спектральный прибор, вообще говоря, не может разделить излучение на двух длинах волн, находящихся в пределах его аппаратной функции).
Сказанного достаточно, чтобы стало ясной необходимость конкретного изучения свойств спектрального прибора, используемого для разложения заданного излучения на монохроматические волны.
1.Дисперсия спектрального аппарата.
Исследуем на какой угол δφ будут разведены диспергирующим элементом два пучка света с длинами волнами 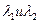 .
.
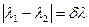
D≡ дисперсия-это функция, характеризуемая производной от угла по длине волны
 (3)
(3)
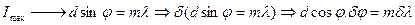
 - угловая дисперсия (4)
- угловая дисперсия (4)
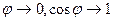 то
то 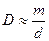 , удобно для оценок только.
, удобно для оценок только.
Следовательно дисперсия дифференциальной решетки тем больше, чем меньше d (период) решетки, т.е. чаще надо наносить штрихи, важно именно число штрихов на единицу длины  , где N-число штрихов, а
, где N-число штрихов, а  длина решетки, и выгодно работать на высоких порядках m,
длина решетки, и выгодно работать на высоких порядках m,  , но в тоже время, m должно превышать
, но в тоже время, m должно превышать  - наибольший порядок дифракции. Например, при
- наибольший порядок дифракции. Например, при  ,
, 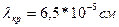 ,
,  - только в первом порядке.
- только в первом порядке.
Здесь n-число единицу длины 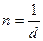
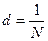
Для λ=1 мкм, следует взять наклонное падение, тогда
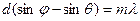

роль угла дифракции 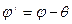 ,
, 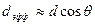 ,
,  ,
,  - скользящее падение для ультрафиолетовых лучей (λ=100Ǻ).
- скользящее падение для ультрафиолетовых лучей (λ=100Ǻ).
Обычно спектр проецируется на экран с помощью линзы. Если ее фокусное расстояние равно f, то угловое смещение будет связано с линейным смещением формулой

таким образом линейная дисперсия  будет равна
будет равна
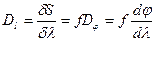 (6)
(6)
она обычно выражается в 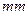 на ангстрем. Часто показывают обратную величину
на ангстрем. Часто показывают обратную величину 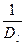 , т.е сколько волн укладывается на 1
, т.е сколько волн укладывается на 1 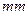

 угол наименьшего отклонения
угол наименьшего отклонения 
A- Преломляющий угол призмы

 где
где 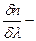

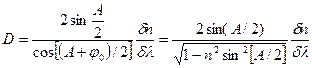 (7)
(7)

Следовательно дисперсия призмы полностью определяется 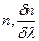 так как для всех прозрачных веществ показатель преломления
так как для всех прозрачных веществ показатель преломления 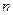 увеличивается с уменьшением длины волны- нормальная дисперсия
увеличивается с уменьшением длины волны- нормальная дисперсия  то выгодно использовать призмы с большим
то выгодно использовать призмы с большим 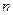 и
и 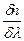 и применять в качестве диспергирующего элемента для коротковолновой. Рис.4. области спектра.
и применять в качестве диспергирующего элемента для коротковолновой. Рис.4. области спектра.
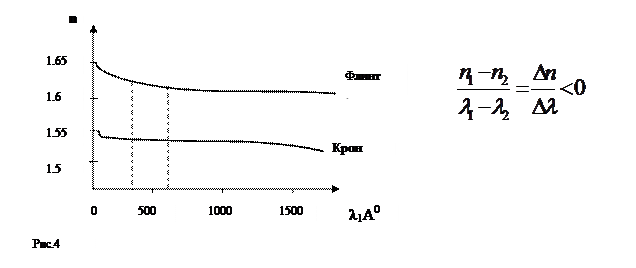
Для ультрафиолетового излучения стекло непрозрачно и призмы обычно изготавливают из кварца. Дисперсия кварцевой призмы для коротких волн  достаточно велика, но при дальнейшем продвижении в ультрафиолетовую область прозрачность кварца заметно уменьшается и для
достаточно велика, но при дальнейшем продвижении в ультрафиолетовую область прозрачность кварца заметно уменьшается и для 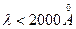 он уже становится полностью непрозрачен.
он уже становится полностью непрозрачен.
Полезно запомнить, что призма наиболее сильно отклоняет фиолетовые лучи, а решетка красные. Для интерферометра Фабри-Перо: 
 ,
, 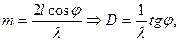 дисперсия
дисперсия  при
при 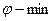 (центральное кольцо).
(центральное кольцо).
2. Явление дисперсии не позволяет полностью охарактеризовать способности спектрального прибора различать произвольное излучение двух близких по длине волн на возможно большое угол, но и добитая того, чтобы каждая составляющая была достаточно узкой.
Разрешающая способность. Эта характеристика дает возможность различать с помощью аппарата две спектральные линии с близкими длинами волн  и
и 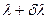 (рис. 5).
(рис. 5).
На рис.5 а. и b представлены две пары  различной ширины, разведенных на один и тоже угол (дисперсия одинаковая), но в одном случае (б) суммарная кривая позволяет наблюдать провал между max, а в другом (а) в излучении нельзя обнаружить две компоненты. Для такой характеристики аппаратной функции, определяющей измерение спектральной линии монохроматического излучения и служит разрешающая сила.
различной ширины, разведенных на один и тоже угол (дисперсия одинаковая), но в одном случае (б) суммарная кривая позволяет наблюдать провал между max, а в другом (а) в излучении нельзя обнаружить две компоненты. Для такой характеристики аппаратной функции, определяющей измерение спектральной линии монохроматического излучения и служит разрешающая сила.

Критерий Рэлея – две спектральные линии могут быть уверенно, разрешены, если max из них (Imax1) приходится на min соседней(Imin2). За меру разрешающей способности принимают отношение длины волны  к min интервалу
к min интервалу 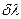

рис. 6

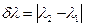 ,
,  – средняя длина волны. Условие возникновения главных max
– средняя длина волны. Условие возникновения главных max  –го порядка для решетки из
–го порядка для решетки из  штрихов для
штрихов для  , для
, для 

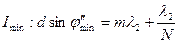
т.к. между двумя главными max,  N -1 min. Для критерия Рэлея
N -1 min. Для критерия Рэлея  , т.е.
, т.е. 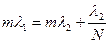
|
|
 или
или 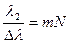 ,
, 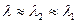 тогда получаем
тогда получаем
Таким образом, разрешающая способность аппарата (дифракционные решетки) зависит от числа штрихов ( ) (для дисперсии от числа штрихов на единицу длинны) т.е. от числа интерферирующих пучков. Поэтому, для повышения
) (для дисперсии от числа штрихов на единицу длинны) т.е. от числа интерферирующих пучков. Поэтому, для повышения  решетки с большой длиной, т.к. еще нужно чтобы
решетки с большой длиной, т.к. еще нужно чтобы 

 (10)
(10)
Тогда  т.е. число длин укладывающихся на разности хода между крайними лучами при максимальном угле дифракции (рис.7).
т.е. число длин укладывающихся на разности хода между крайними лучами при максимальном угле дифракции (рис.7).

Разрешающая сила решетки всегда меньше длины ее рабочей части и следует учесть, что Im ~  ограничение на высокие
ограничение на высокие  .
.
 , и
, и  (11)
(11)
3. Область свободной дисперсии 
 (12)
(12)
под выбранным углом  распространяется измерение не только определенной длины волны
распространяется измерение не только определенной длины волны  , но и других волн
, но и других волн 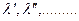
Так, например, в одном направлении  будет распространятся излучение с длиной волны 6000А0(1ый порядок), 3000А0(2ой порядок) и 2000А0(3ий порядок) и т.д. (
будет распространятся излучение с длиной волны 6000А0(1ый порядок), 3000А0(2ой порядок) и 2000А0(3ий порядок) и т.д. ( . Пусть на решетку падают волны в интервале
. Пусть на решетку падают волны в интервале 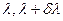 ,
,
max 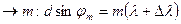 для правого края
для правого края
max 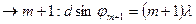 для левого края
для левого края
|
|
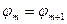 ,
, 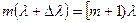 или
или
Таким образом дисперсионная область уменьшается с увеличением порядка. Разрешающая способность призмы запишем без доказательство:
А=  , (где b– основные призмы) (14)
, (где b– основные призмы) (14)
для призмы  только m =1
только m =1
Гораздо шире распространен случай, когда коэффициент пропускания пластинки, располагаемой в световом пучке, меняется не в доль одного направления, а по всей поверхности пластинки. Такая структура будет двумерной (двумерная решетка). Этот случай практически очень важен.
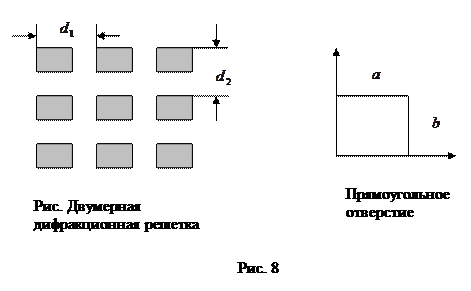

Очевидно что
 (15)
(15)
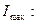
 (16) (
(16) ( – направляющий
– направляющий  )
)
Пусть на такую систему дважды дифракционных решеток падает плоская волна. Обозначим через  углы между нормалью к падающей волны и осями
углы между нормалью к падающей волны и осями 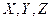 . Рассмотрим случай нормального падения (
. Рассмотрим случай нормального падения ( ). Условия возникновения главных
). Условия возникновения главных  для излучения с любой произвольной длиной волны имеют вид
для излучения с любой произвольной длиной волны имеют вид
 17(
17(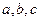 )
)
Интенсивность от щели на прямоугольном отверстии (рис.8) (сделали переход от дифракций на двухмерной решетки к щели на прямоугольном отверстии). В направлении углов 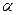 и
и  дает выражение (аналогично прямоугольной щели)
дает выражение (аналогично прямоугольной щели)
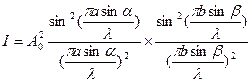 (18)
(18)
Анализ показывает, что главные  возникают тогда, когда
возникают тогда, когда 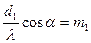 и
и 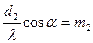 ,
, 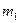 и
и  – целые числа. В этом случае если
– целые числа. В этом случае если  и
и  – число штрихов на двухмерной решетки вдоль
– число штрихов на двухмерной решетки вдоль  соответственно, то
соответственно, то

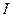 ~
~ 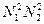 (19)
(19)
Если только 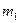 или
или  целое, то главное
целое, то главное  имеет
имеет 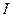 много меньше.
много меньше.
ричс 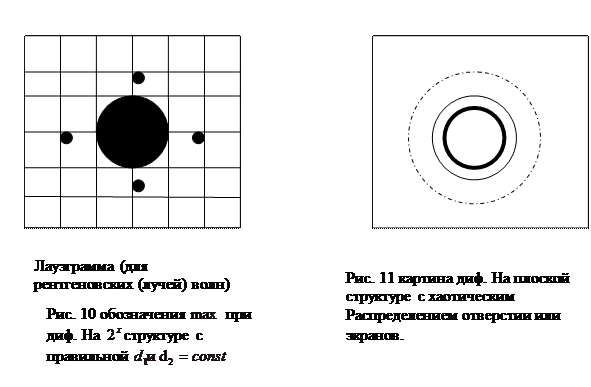
Итак, анализ рис.10 и рис.11 дает возможность экспериментально отличить правильное расположение вызывающих дифракцию центров от хаотического их распределение. Это особенно интересно, если в качестве решетки выступает кристаллическая решетка твердого тела, которая представляет собой пространственную структуру. При падении на нее излучение с очень малой длиной  волны, например (рентгеновской), будет наблюдаться дифракция. Большой интерес и практическое значение имеет дифракция на пространственных неоднородностях. В этом случае волна распространяется не в однородной среде, а в среде, в которую включены участки, где скорость волны отличается от скорости в остальных частях среды, т.е.
волны, например (рентгеновской), будет наблюдаться дифракция. Большой интерес и практическое значение имеет дифракция на пространственных неоднородностях. В этом случае волна распространяется не в однородной среде, а в среде, в которую включены участки, где скорость волны отличается от скорости в остальных частях среды, т.е.  . Если
. Если 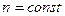 в среде, то волна остается плоской (как и падающая). Если и ее однородность среды нарушено какими либо включениями или в следствии каких либо процессов, т.е.
в среде, то волна остается плоской (как и падающая). Если и ее однородность среды нарушено какими либо включениями или в следствии каких либо процессов, т.е. 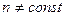 (локально), то на таких неоднородностях должны возникнуть дифракционные явления, и часть света дифрагирует (отклоняется) от своего первоначального направления, и поверхность одинаковой фазы перестает быть плоским, и свет будет распространяться по различным направлениям.
(локально), то на таких неоднородностях должны возникнуть дифракционные явления, и часть света дифрагирует (отклоняется) от своего первоначального направления, и поверхность одинаковой фазы перестает быть плоским, и свет будет распространяться по различным направлениям.
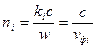 (20)
(20)
С такими дифракционными явлениями мы встречаемся в природе: распространение света в тумане (ориентировка судов, и явление Тиндаля, 1860г.) при прохождение света в мутных средах, дым или другие твердые частицы, взвешенные в газе взвесь нерастворяющихся жидкостей. Известно, что интегральное интенсивность излучения диполя пропорциональна четвертой степени частоты (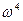 ~
~ 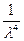 ). Следовательно, голубой цвет будет рассеиваться значительно сильней красного
). Следовательно, голубой цвет будет рассеиваться значительно сильней красного 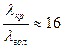 . это так называемое молекулярное рассеяние. Яркий пример этому – возникновение голубого небо в результате рассеяние солнечного света (рассеивание на флуктуациях плотности в атмосфере); венцы вокруг солнца представляют дифракционные явления – их внешний край красного света, тогда как гало (светлые круги вокруг солнце) возникают в результате преломления световых лучей на кристаллах льда в атмосфере, а также круги (гало и венцы) вокруг луны.
. это так называемое молекулярное рассеяние. Яркий пример этому – возникновение голубого небо в результате рассеяние солнечного света (рассеивание на флуктуациях плотности в атмосфере); венцы вокруг солнца представляют дифракционные явления – их внешний край красного света, тогда как гало (светлые круги вокруг солнце) возникают в результате преломления световых лучей на кристаллах льда в атмосфере, а также круги (гало и венцы) вокруг луны.
Явление дифракций на пространственных препятствиях или неоднородностях, когда число таких неоднородностей очень велико, а размеры их незначительны очень легко наблюдать. В таком случае среду принято называть мутной, и явление дифракции носит обычно название рассеяние света. "Молекулярное мутность" есть результат случайного скопления значительного числа молекул, образующегося при беспорядочном тепловом движении. Отметим, что для волн обычного света молекулярное строение среды само по себе еще не обуславливает неоднородности, т.к.  >>
>> 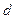 молекул (10-8 см). наоборот, для волн очень коротких (
молекул (10-8 см). наоборот, для волн очень коротких (
 ) рентгеновских, уже само наличие молекул обусловливает неоднородность среды и ведет к дифракции (рассеянию). Рассмотрим дифракцию на трехмерных периодических структурах (случай ромбических кристаллов), которую можно описать формулами для решетки с добавлением условия
) рентгеновских, уже само наличие молекул обусловливает неоднородность среды и ведет к дифракции (рассеянию). Рассмотрим дифракцию на трехмерных периодических структурах (случай ромбических кристаллов), которую можно описать формулами для решетки с добавлением условия  в результате интерференции лучей, идущих от разных плоскостей решетки (рис.12) свет на решетку падает снизу. По направлению
в результате интерференции лучей, идущих от разных плоскостей решетки (рис.12) свет на решетку падает снизу. По направлению 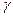 идут лучи 1 и 2 диофрагированные на двух плоскостях
идут лучи 1 и 2 диофрагированные на двух плоскостях
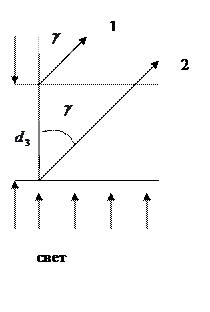
(21) 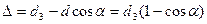 , где
, где 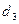 – третий период решетки, тогда
– третий период решетки, тогда
(22)  и
и 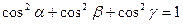
Система (22) – определяет дифракционные условия 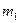 ,
,  и
и 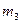 – целые числа. Не трудно видеть, что нельзя, вообще говоря, для любой длины волны получить направление (
– целые числа. Не трудно видеть, что нельзя, вообще говоря, для любой длины волны получить направление ( ) для которого выполняются все эти условия. Действительно, исключая из этих уравнений
) для которого выполняются все эти условия. Действительно, исключая из этих уравнений  найдем соотношение
найдем соотношение
 (23)
(23)
Который показывает, какие значения должна иметь длина волны  для того, чтобы в данной структуры при заданном первоначальном направлении распространение света образовались отчетливые дифракционные максимумы. Таким образом, на пространственной дифракционной решетке получается дифракционный
для того, чтобы в данной структуры при заданном первоначальном направлении распространение света образовались отчетливые дифракционные максимумы. Таким образом, на пространственной дифракционной решетке получается дифракционный  только для некоторых длин волн, удовлетворяющих условию (23). В применении к дифракций рентгеновских лучей на кристаллах получение соотношение называются формулами Лауэ (1913г.).
только для некоторых длин волн, удовлетворяющих условию (23). В применении к дифракций рентгеновских лучей на кристаллах получение соотношение называются формулами Лауэ (1913г.).
Если происходит отражение от слоев решетки, то интерференционное соотношение имеет тот же вид что и формула разности хода для плоскопараллельной пластинки (рис.13)

 (24)
(24)
Где  – угол скольжения
– угол скольжения

Это соотношение обычно называется условием Брега–Вульфа. Оно позволяет на опыте определить расстояние между плоскостями, в которых находится максимальное число исследуемых центров. Кроме того, если для данного кристалла точно известны расстояния между отражающими плоскостями, то это соотношение можно использовать для определения длины волны рентгеновского излучения.
Date: 2016-07-25; view: 490; Нарушение авторских прав


