
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Общая интерференционная схема.
|
|
Интерференция света.
Лекция №2.
Когерентность. Интерференция колебаний.
Пусть в некоторой точке пространства Р одновременно существуют две произвольные волны (в общем случае немонохроматические). Согласно принципу суперпозиции, напряженность электрического поля. Для перехода к энергетическому описанию возведем это равенство в квадрат:
 (2.1)
(2.1)
Так как трудно осуществить безынерционное измерение процессов длительностью = время пребывания атома в возбужденном состоянии (0.1 с – инерционность зрительного восприятия человека). Поэтому надо усреднить уравнение (2.1)

 (2.2)
(2.2)
или вводя  =a2 =I, где I- интенсивность волны. Тогда средняя суммарная энергия
=a2 =I, где I- интенсивность волны. Тогда средняя суммарная энергия  зависит от:
зависит от:  интерференционного члена
интерференционного члена 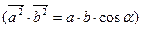
Случай 1) I= I1 +I2  (2.3) 2)I≠ I1+I2 (2.4)
(2.3) 2)I≠ I1+I2 (2.4)


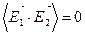
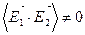
1) Суммарная освещенность равна сумме освещенностей.
2) Суммарная освещенность не равна сумме освещенностей (имеет место интерференция) 
Геометрическая интерпретация сложения двух векторов.

 (2.5)
(2.5)
Если за время t/ разность фаз ( ) много раз изменялось то
) много раз изменялось то  (2.6). Тогда необходимое условие существования интерференции:
(2.6). Тогда необходимое условие существования интерференции:
Определение. Для возникновения интерференции необходимо, чтобы разность фаз  const за время усреднения.
const за время усреднения.
В этом случае колебания называются когерентными. Т.е. сложение колебаний, при котором не имеет место суммирование интенсивностей (случай 2), называется интерференцией колебаний.
 (2.7)
(2.7)
Из (2.7) видно, два гармонических колебания одной частоты всегда когерентны. Гармонические колебания порождают монохроматические волны, способные интерферировать. Равенство частот интерферирующих волн 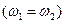 и неперпендикулярность векторов
и неперпендикулярность векторов  и
и  служат дополнительными требованиями. С учетом этого условие (2.7) является достаточным.
служат дополнительными требованиями. С учетом этого условие (2.7) является достаточным.
При
 может наблюдаться нестационарная интерференционная картина.
может наблюдаться нестационарная интерференционная картина.
Для негармонических колебаний наличие корреляции фаз служит необходимым условием их когерентности.
При описании интерференционных явлений - понятие временной и пространственной когерентности. Временную когерентность обычно связывают со степенью монохроматичности исследуемых колебаний, а степенью пространственной когерентности характеризуют геометрию экспериментов (протяженный источник света).
Результат интерференции определяется разностью фаз интерферирующих волн в месте наблюдения, которая зависит от начальной разности фаз, а также от разности расстояний, отделяющих точку наблюдения от источников каждой из волн.
 P
P
 S1 r1
S1 r1
S 2l
S2
Пусть  для простоты вычислений
для простоты вычислений  (2.8)
(2.8)
(D>>2l),  (2.9)
(2.9)
(задача скалярна, т.к. все колебания направлены одинаково).
Считая ∆= r2-r1 (разность хода или геометрическая разность хода), I=a2=E2 (2.10)
 , (2.11)
, (2.11)
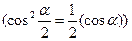 ,
,
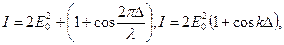 т.к.
т.к.  (2.12)
(2.12)

Imax: Imax= 4E  при k∆= 2mπ – четный,
при k∆= 2mπ – четный,

Imin: Imin=0 при k∆= (2m+1)π – нечетный,
где m – порядок интерференции, m= 0, 1, 2 …

 kΔ=
kΔ=  ,где 2m – четное число (2.13)
,где 2m – четное число (2.13)
(2m+1)- нечетное число,  (2.14)
(2.14)
Если одна из волн проходит в среде с показателем преломления n1, то вводят понятие оптической разности хода (разность произведений rini).

 (2.15)
(2.15)
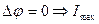 (собирающая линза)
(собирающая линза)
С другой стороны Δ можно определить из геометр. рисунка ΔS1S2A~ΔNPO/ отсюда

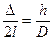 или
или  (2.15а)
(2.15а)
Следовательно, 
На экране чередование светлых и тёмных полос.


 - ширина полосы (2.16)
- ширина полосы (2.16)
Для количественной характеристики качества интерференционной картины вводят функцию видимости, качество интерференционных полос существенно зависит от освещенности (Майкельсон).
 , где 0≤V≤1 (2.17)
, где 0≤V≤1 (2.17)
Если  , n=const,
, n=const, 
 P
P
r1
O1
r2
O2 Δr << 1
 - сдвиг начала отсчета,
- сдвиг начала отсчета,

Тогда величину 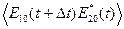 называют функцией корреляции, а
называют функцией корреляции, а
 - комплексная степень когерентности излучаемых колебаний.
- комплексная степень когерентности излучаемых колебаний.

Другими словами  - это доля когерентности света
- это доля когерентности света
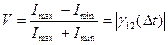 (2.17)
(2.17)
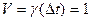 - полная когерентность двух рас. колебаний.
- полная когерентность двух рас. колебаний.
___________________________________________________________________________________
τизл, τуд, τког, Lког.
τког (10-9-10-10с), Lког = Сτког.
Δ<Cτког => интерф. картина, τког для обычных источников (не лазеров) 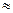 3-30 см
3-30 см
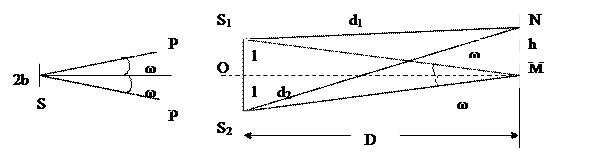
Lког (в радиотехнике) 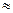 10// км
10// км
___________________________________________________________________________________
Опыт показывает, что когда два независимых источника света, например, две свечи, или даже два различных участка донного и того же светящегося тела посылают световые волны в одну область пространства, то мы не наблюдаем, интерференции и имеем сложение интенсивностей I=I1+I2.Сказанное не относится к лазерным источникам.
1. Бизеркала Френеля.


Для получения двух систем когерентных волн необходимо испускаемое излучение расчленить на два потока (путем отражения или преломления) и заставить их встретиться после того, как они пройдут различные пути d1 и d2.
2. Билинзы Бийе.
 В интерференционном поле, благодаря интерференции, происходит перераспределение освещенности – образуются интерференционные полосы. Углы 2ω, идущие от S – угол раскрытия лучей апертура интерференции световой поток Φ = ВδΩ, яркость В задается.
В интерференционном поле, благодаря интерференции, происходит перераспределение освещенности – образуются интерференционные полосы. Углы 2ω, идущие от S – угол раскрытия лучей апертура интерференции световой поток Φ = ВδΩ, яркость В задается.

3. Бипризма Френеля.


 S1 и S2 – мнимые источники. Δ│r1-r2│<cτког , угол PSP=2ω- апертура интерференции, угол BS1R равен углу LS2F=2γ- апертура перекрывающихся пучков для бесконечно удаленного экрана.
S1 и S2 – мнимые источники. Δ│r1-r2│<cτког , угол PSP=2ω- апертура интерференции, угол BS1R равен углу LS2F=2γ- апертура перекрывающихся пучков для бесконечно удаленного экрана.
Апертура интерференции 2ω=  2ω<2γ. Преломляющие углы бипризмы делают очень маленькими, чтобы S1S2, маленькими, и, следовательно широкие полосы на экране
2ω<2γ. Преломляющие углы бипризмы делают очень маленькими, чтобы S1S2, маленькими, и, следовательно широкие полосы на экране  .
.
4. Зеркало Ллойда.
В отличие, от схем Френеля, апертура интерференции 2ω сильно зависит от того, для какого места на экране исследуется интерференция. Она тем меньше 2ω<2ω/ чем ближе это место к центру поля. С ростом h качество падает.

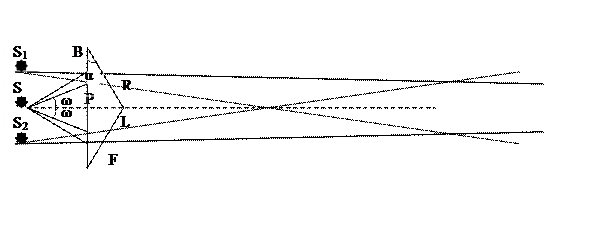
Общая интерференционная схема.
S1S2=2l, OM=D, S1N=d1, S2N=d2, S1 и S2 – синфазны, центральный max лежит в М, S1M-S2M=0.
Δ=d2-d1 до любой точки N, лежащей на расстоянии h от М




Δ- разность хода в длинах волн.
 Из формулы (2.12)
Из формулы (2.12)
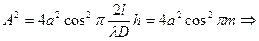
Imax при m= (0, 1, 2..),
Imin при m= (1/2, 3/2..).
Расстояние между соседними max и min, соответствует изменению m на единицу



 (2.18)
(2.18)
|
 Ширина полосы уменьшается с увеличением
Ширина полосы уменьшается с увеличением  при D и λ= const. Ширину полосы можно выразить через апертуру интерференции, так как угол 2ω мал, то есть tg2ω ≈ sin2ω ≈ 2ω, тогда
при D и λ= const. Ширину полосы можно выразить через апертуру интерференции, так как угол 2ω мал, то есть tg2ω ≈ sin2ω ≈ 2ω, тогда 
Угловое расстояние между двумя соседними max или min

Date: 2016-07-25; view: 2103; Нарушение авторских прав