Возможность наблюдения интерференции от протяженного источника.

При наличии двух независимых (некогерентных) источников света можно получить две стационарные интерференционные картины и с помощью какого-нибудь оптического устройства свести их в некоторой области пространства.

В результате наложения двух интерференционных картин может наблюдаться I_max≠I_min или

I_max=I_min (0≤V≤1).

Рассчитаем, как будет зависеть функция видимости от геометрии эксперимента. Возьмем две самосветящиеся щели S₁ и S₂, перпендикулярные плоскости рисунка, экран параллельно плоскости, в которой лежат S₁ и S₂. разделим пучок, излучаемый S₁ (и соответственно S₂), на два с помощью двух параллельных зеркал. Следовательно, каждый реальный источник света заменяется двумя фиктивными. Вместо S₁ мы получим два когерентных источника и , вместо S₂- и . Расстояние .Для того, чтобы использовать все выкладки, проделанные ранее, надо чтобы D>>2l, D>>2d и (2.20) и апертура интерференции 2ω весьма мала sin2ω≈2ω.

Тогда из формул (2.11), (2.13), (2.15) , 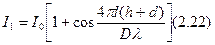суммарная интенсивность I=I₁+I₂ (ни какой интерференции нет, так как S₁ и S₂ не когерентны) . (2.23)

так как ,

, I=f(h) (2.24)

Из формулы (2.24)=> I_max будет (если )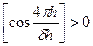

I_min будет (если )

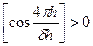(2.25)

Отсюда функция V: (2.26)

V→1 при 2d<<δh (cos0=1),

V→0 при 2d= δh/2- полосы на экране исчезнут,

V→1 при 2d= δh,

V→0 при 2d= 3δh/2.

Теперь пусть весь промежуток 2d занимает один протяженный источник света (на экране средняя освещенность I₀). Разобьем его мысленно на светящиеся полоски шириной δξ<<λ (такие элементарные источники будут не когерентны). В любой точке экрана .

На экране будут наблюдаться полосы в зависимости от h формулы (2.27)

или , при x→0, , а с увеличением x монотонно убывает, при x= π, V= 0 затем опять возрастает по функции меньшего экстремального значения, при x= 2π, V=0 опять и т.д. V=2/3 при 2d =δh/2. При V≥2/3, I_max≥5I_min при 2d ≤ δh/2, .

Получаем искомую связь между дополнительными размерами источника (с длиной волны λ), и апертурой интерференции

(2.29)

1)Чем меньше ω (апертура интерференции), тем больше допустимые размеры источника.

2)Формула (2.29): мы получили право использовать синусоидальную модеализацию и для протяженного источника.

3)Δ<cτ_ког остаётся в силе и для протяженного источника, а условие временной когерентности дополняется условием пространственной когерентности (2.29), которую можно вычислить:

(2.30)

Стоячие световые волны. Опыты Винера.

Условия интерференции между падающей и отраженной волнами сходны для волн любых типов. Существенным является то, что в процессе отражения может иметь место изменение фазы волны.

S₁ = a sin (ώt – x) (2.31)

S₂ = a sin (ώt + x + δ) (2.32)

где ώ = , , отражение в точке х = 0.

S_R = S₁ + S₂ = 2a cos ( x + 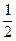δ) sin (ώt + 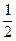δ) (2.33)

A = f(x) = 2a cos ( x + 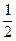δ) = 2a cos ( x + 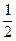δ) (2.34)

Знак амплитуды остается неизменным в пределах полуволны и меняется на противоположный при изменении х на .

при δ = 0 а > 0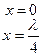

Опр. т.е. фаза колебаний остается постоянной в пределах полуволны и меняется на π при переходе от одной к другой – определение стоячей волны.

А = 0 при kx + 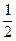δ = 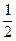nπ, n = 1, 3, 5… нечетные числа, эти точки расположены на расстоянии (полуволны) одна от другой и называются узлами стоячей волны. Между узлами посредине, A_max = 2a и называются пучностями. kx + 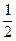δ = 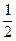nπ, n =0, 2, 4… - четные числа.

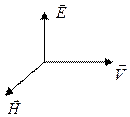
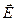
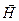
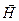
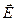
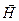
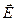
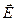
ε₂ > ε₁ ε₂<ε₁

в падающей в отраженной

Так как при отражении изменилось направление , а 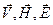должны образовывать правовинтовую систему, то один из векторов должен скачками поменять свое направление на противоположное, т.е. получить добавочное изменение фазы на π или, как говорят, испытать потерю полуволны. В зависимости от условий на границе двух сред. Если ε₂>ε₁ то для H δ = 0, для E δ = π и если ε₂<ε₁ то для H δ = π, для E δ = 0. Различие в δ ведет к тому, что узлы одного из векторов совпадают с пучностями другого.

(2.35)

Моменты прохождения через max вектора 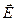и 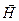отличаются на четверть периода. Энергия стоячей волны (СВ) локализована и переходит от области пучности 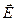к области пучности (т.е. обращается в магнитную). Следовательно, вместо течения энергии мы имеем дело с колебаниями ее, переход энергии из одной формы в другую.

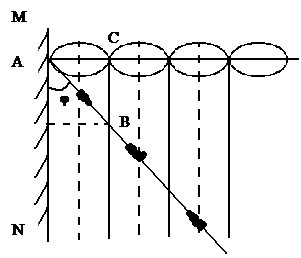Опыт Винера. (прием «малого наклона»)

Система стоячих волн получалась в воздухе при отражении монохроматического света от металлического зеркала. Положение очень тонкого (около 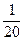λ) светочувствительного слоя, образующий малый угол φ с поверхностью MN светочувствительный слой пересекается с плоскостями пучностей или иной силы по параллельным прямым, след от которых изображен на рисунке в виде черных пятен.

AB = AC/sin φ = 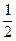λ/sin φ = (2.36)

Если φ достаточно мало, то АВ становится достаточно большим. φ = 1´ => AB ≈ 1 ÷ 2 мм. При этих условиях можно заметить, что первая четная полоса не совпадает с ним, а отстоит от него на .

Опыт Винера, позволивший впервые получить стоячие световые волны и доказать, что фотографическое действие световой волны связано с ее электрическим вектором.

Т.к. электроны входят в состав атомов и молекул и представляют собой электрические заряды, то сила действующая на них, определяется в первую очередь электрическим полем, т.е. электрическим вектором э/м волны. Магнитный вектор играет лишь второстепенную роль (здесь) и действие его непосредственно почти не сказывается.

Date: 2016-07-25; view: 638; Нарушение авторских прав