
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Вращение плоскости поляризации
|
|
Вещества, обладающие способностью вращать плоскость поляризации, называются оптически активными.(кристаллы и аморфные тела)
1.опыт с кварцем, одноосный кристалл.
| 
Поляризатор (Р1) и анализатор (Р2) установлены так, что не пропускают излучения (скрещены). После введения пластинки из кварца толщиной d поле просветляется. Свет распространяется вдоль оптической оси => двойное лучепреломление отсутствует. Повернув анализатор на угол φ, снова получаем темноту => доказательство поворота плоскости поляризации, а не какого-то другого явления. Разные образцы вращают плоскость поляризации вправо = правое вращение (по часовой стрелке) или влево = левое вращение (против часовой стрелки), такие кристаллы отличаются по своей форме и являются зеркальным отображением друг друга.
Опыт дает:  ,
, 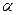 ~
~  (т. е. сильно зависит от λ) (1)
(т. е. сильно зависит от λ) (1)
Например: при d= 1 мм имеем  , а
, а 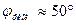
2. опыт с аморфными веществами - сахар, камфара, никотин и др.
угол поворота =  , где
, где  - концентрация (2)
- концентрация (2)
[α]~  -постоянная вращения для данного вещества.
-постоянная вращения для данного вещества.
Этот метод используют для нахождения, например, концентрации сахара в производственных растворах и биологических веществах (кровь, моча). Угол поворота плоскости поляризации φ можно измерить с большой точностью (~0,01º).
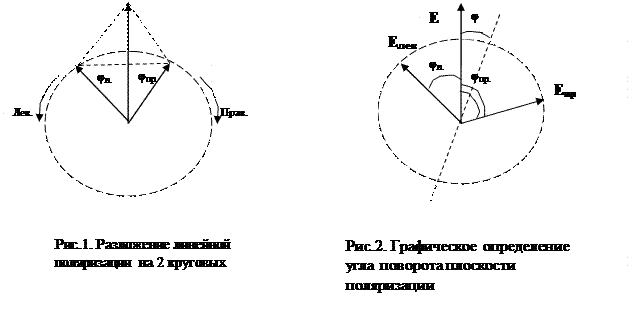
Френель: любое линейно поляризованное колебание можно разложить на два круговых колебания с правым и левым вращением (Рис.1). в оптически активном веществе скорость распространения волны с левым вращением отлична от волны с правым вращением, uпр  uлев=>nпр
uлев=>nпр  n. (“правые” nпр>nлев и т.п.)
n. (“правые” nпр>nлев и т.п.)
Следовательно, время, необходимое каждой волне для прохождения одного и того же расстояния (d) в активной среде, окажется различным => векторы  и
и 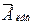 повернутся на разные углы φпр и φлев (Рис.2). => для того чтобы результирующее колебание оставалось линейным, неизбежно должна повернуться плоскость симметрии. Плоскость колебаний вектора в результирующей плоско поляризованной волне повернется по отношению к направлению колебаний в исходной волне на угол
повернутся на разные углы φпр и φлев (Рис.2). => для того чтобы результирующее колебание оставалось линейным, неизбежно должна повернуться плоскость симметрии. Плоскость колебаний вектора в результирующей плоско поляризованной волне повернется по отношению к направлению колебаний в исходной волне на угол  (3)
(3)
Если линейно поляризованная волна описывается как  (4)
(4)
Если по кругу, то  (5)
(5)
Т.к. exp(i*π/2)=i, то появление разности фаз δ=π/2 между Ex и Ey эквивалентно умножению одной из них на i, а знак “± “ соответствует правому или левому вращению, при правом вращении Ey опережает Ex на π/2,
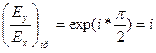 и
и 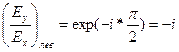 (6)
(6)
Следовательно [учитывая, что cos(α+ 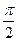 )=-sinα] имеем
)=-sinα] имеем
 }правое вращение
}правое вращение 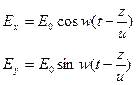
 }левое вращение (7)
}левое вращение (7)
Для неактивных веществ nпр = nлев ; uпр = uлев =u
Для активных веществ nпр  nлев.
nлев.
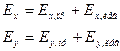 } и вместо E0 =>
} и вместо E0 => 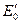 ,
, 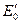 <E0, [
<E0, [  ]
]
Тогда Ex= 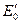
 +
+ 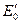
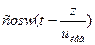 ={2
={2  (8) Ey=
(8) Ey=  (9)
(9)
Сравнивая (8) и (9) => что фазы колебаний Exи Ey одинаковы => сдвиг фаз δ=0 и => при сложении этих колебаний => линейно поляризованная волна. При прохождении z = d, плоскость поляризации повернется на угол φ.
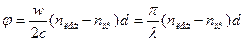 (10)
(10)
∆n=nлев-nпр, если 
 см, d= 10cм, то ∆n~
см, d= 10cм, то ∆n~  ,
,
т. е. можно обнаружить ничтожную разницу в показателях преломления.
С позиции молекулярной теории вращение ПП (плоскости поляризации) связано с асимметрией строение оптически активного вещества. Для кристаллов главной причиной различая скоростей из-за асимметрии внешней формы (отсутствие центра симметрии), для аморфных сред – со строением сложных молекул активных сред.
 | |||
 |
Асимметричные молекулы. Борн (1915) показал, что ВПП можно объяснить если учесть взаимодействие э/м поля с веществом в пределах одной молекулы. Все активные вещества характеризуются правым и левым вращением ПП, рассматривались сложные асимметричные молекулы с пространственной структурой, не имеющие ни центра симметрии, ни плоскости симметрии. Рис. 3 – отрезок спирали. Δn будет зависеть от размеров молекулы. При проведении расчета предполагается наличие определенных соотношений между электрическими моментами, вызываемыми линейно поляризованной волной в разных участках (радикалах) изучаемой сложной молекулы, и учитывалось изменение фазы волны в ее пределах.
Δn = nпр – nлев = 4πγ sin 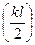 (11)
(11)
γ – некоторая const,  , так при l = 0 => Δn = 0 – нет вращения ПП.
, так при l = 0 => Δn = 0 – нет вращения ПП.
Пример: УКВ-излучение, λ ≈ 3 см (клистрон). На пути волны ставится небольшая коробка из бумаги с хаотически расположенными внутри отрезками спирали (a = 6÷7 мм, длиной ≈ 10 мм) из медной проволоки. Рупор приемника излучения составляет угол  с рупором излучателя. Введение коробки приводит к появлению сигнала, повернув приемник на угол φ, можно опять погасить сигнал => наблюдается вращение ПП.
с рупором излучателя. Введение коробки приводит к появлению сигнала, повернув приемник на угол φ, можно опять погасить сигнал => наблюдается вращение ПП.
Механизм магнитного вращения плоскости поляризации (МВПП)
 Опыт Фарадея:
Опыт Фарадея:
Между скрещенными поляризаторами вводят оптически неактивное вещество, помещенное внутрь катушки с большим числом витков (H = μμ0nI), при включении тока внутри катушки возникает магнитное поле (продольное) и на экране наблюдается светлое пятно => свет от скрещенных поляризаторов проходит, если выключить поле Н, то пятно исчезнет =>  эффект МВПП. Важной особенностью МВПП является малая инерционность (10-9).
эффект МВПП. Важной особенностью МВПП является малая инерционность (10-9).
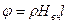 (12)
(12)
ρ = const Верде.
МВПП. Важной особенностью МВПП является малая инерционность (10-9).
При изучении явления => учесть действие э/м волны на излучающий электрон.


 (13)
(13)
 =>}
=>}  (14)
(14)
На входе (z= 0)
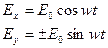 }
} 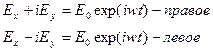 вращение
вращение
Решение уравнения (13) ищем в виде:

 (15) => r0- вещественно, т.к. поглощение отсутствует, а магнитное поле лишь изменяет направление движения зарядов, но не тормозит.
(15) => r0- вещественно, т.к. поглощение отсутствует, а магнитное поле лишь изменяет направление движения зарядов, но не тормозит.
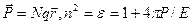
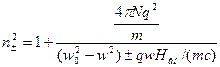 (16) => две волны (±), => nпр и nлев непосредственно связаны с ± qwHвн/(mc), что и требовалось доказать.
(16) => две волны (±), => nпр и nлев непосредственно связаны с ± qwHвн/(mc), что и требовалось доказать.
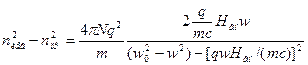
 и пренебрегая
и пренебрегая  =>
=>
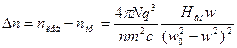 => если Hвн=0, то и ∆n=0
=> если Hвн=0, то и ∆n=0
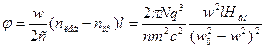 (17)
(17)
и const Верде 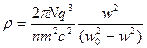 , ρ~
, ρ~ 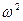 ~
~  ,
, 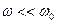
Удобно записывать const Верде в виде  (18)
(18)
 Нормальный эффект Зеемана.
Нормальный эффект Зеемана.
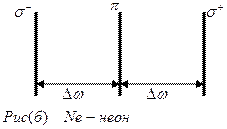 При нормальном эффекте Зеемана линия расщепляется на две компоненты, если наблюдение ведется вдоль поля (Рис. а) или на три, если ведется перпендикулярно магнитным силовым линиям (Рис. б). опыт показывает, что смещенные компоненты поляризованы по правому σ+ и левому σ- кругам, а несмещенная π-компонента линейно поляризована в продольном
При нормальном эффекте Зеемана линия расщепляется на две компоненты, если наблюдение ведется вдоль поля (Рис. а) или на три, если ведется перпендикулярно магнитным силовым линиям (Рис. б). опыт показывает, что смещенные компоненты поляризованы по правому σ+ и левому σ- кругам, а несмещенная π-компонента линейно поляризована в продольном 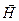 .
.
 |
Расщепление линии испускания 


Решение ищем в виде: 

Положим 
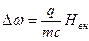 (вдоль поля).
(вдоль поля).
Линия испускания расщепится на две поляризованных по кругу σлев- и σпр+ компоненты смещенные относительно ω0 на 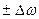 . В центре, где при
. В центре, где при 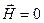 находилась бы исследуемая спектральная линия, не будет наблюдаться никакого излучения.
находилась бы исследуемая спектральная линия, не будет наблюдаться никакого излучения.
 Из графика => 1 – в узком спектральном интервале вблизи линии поглощения дважды меняется знак эф. Фарадея угол вращеня ПП имеет один знак вне интервала
Из графика => 1 – в узком спектральном интервале вблизи линии поглощения дважды меняется знак эф. Фарадея угол вращеня ПП имеет один знак вне интервала  , и другой внутри. => 2 – угол вращения вблизи поглощения может быть очень большим, т.к. происходит резкое изменение n и коэф. поглощения и разность
, и другой внутри. => 2 – угол вращения вблизи поглощения может быть очень большим, т.к. происходит резкое изменение n и коэф. поглощения и разность  может принимать большие значения.
может принимать большие значения.
Date: 2016-07-25; view: 572; Нарушение авторских прав