Методика анализа графика зависимости дисперсии от времени.

Связь между дисперсией объединенного процесса и масштабом агрегации формулируется как (8.1), что эквивалентно (9.1).

(9.1)

Прологарифмировав обе части (9.1) получают зависимость:

(9.2)

Следовательно, можно получить оценку , вычислив для различных значений и отображая результаты графически от , провести через полученные точки прямую линию по методу наименьших квадратов. Оценку для определяют как отрицательный наклон прямой линии, подобранный по методу наименьших квадратов. График зависимости Var[X(m)] от в двойном логарифмическом масштабе будет представлять собой прямую линию с наклоном . Примеры зависимости дисперсии агрегированных выборок приведены на рис. 9.1.

Рисунок 9.1 – Зависимость дисперсии агрегированного процесса от времени (слева), аппроксимирующая прямая (справа)

Методика оценки параметра Херста по R/S статистике. Статистическое самоподобие означает, что статистические свойства одинаковы и для всего набора данных, и для подразделов набора данных (две части набора данных имеют такие же статистические свойства, как и весь набор данных). Это применяется к оценке экспоненты Херста, где нормированный диапазон оценивается на различных участках. Нормированный диапазон рассчитывается для всего набора данных. Затем нормированный диапазон рассчитывается для двух частей набора данных, результирующие и . Этот процесс продолжается путем деления каждого из предыдущих разделов на две части и расчета нормированного диапазона для каждого нового раздела. Нормированные диапазоны значений для каждого раздела усредняются. Деление прекращается, когда область становится слишком мала (менее 8 точек). Параметр Херста оценивается путем расчета среднего нормированного диапазона в нескольких областях данных. Для данного набора наблюдений, с выборочным средним определяется последовательностью скорректированных частичных сумм:

(9.3)

(9.4)

Диапазон определяется по формуле:

(9.5)

Параметр Херста определяется заданным нормированным диапазоном:

(9.6)

при Н >0.5

Рисунок 9.2 – График R/S статистики при H=0.7

Методика оценки параметра Херста по методу периодограмм (рис. 9.3). R/S-метод дает лишь приближенное значение показателя Херста, поэтому для его вычисления целесообразно пользоваться несколькими методиками и сравнения полученных результатов. Рассмотрим метод определения величины на основе периодограммного анализа. Для самоподобного СП вычисляется периодограмма

(9.7)

где – частота;
N – количество элементов во временной серии X.

Для самоподобных процессов

(9.8)

Оценочная формула Уитла:

(9.9)

– СПМ фрактального шума

Рисунок 9.3 – Периодограмма самоподобного процесса (H=0.7)

Методика вычисления параметра Херста по МДА (рис. 9.4).

1. Рассчитать

(9.10)

2. Определить средний угол наклона в двойном логарифмическом масштабе.

3. Проверить, что .

4. Вычислить .

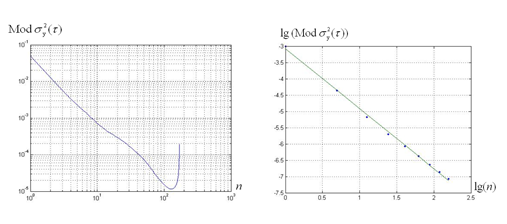
Рисунок 9.3 – Графики зависимости МДА от n при H =0.8

Рисунок 9.4 – Сравнение некоторых методов оценки

Рисунок 9.5 – Погрешности методик оценки параметра Хэрста

Влияние самоподобия трафика на работу телекоммуникационных систем:

Размер буфера коммутатора расчитывается по следующей формуле:

(9.11)

Рисунок 9.6 – Зависимость размера буфера коммутатора от коэффициента использования

Date: 2016-07-25; view: 333; Нарушение авторских прав