Показательное (экспоненциальное) распределение.

Вернемся к рассмотрению простейшего потока событий с интенсивностью а (см. распределение Пуассона) и введем непрерывную случайную величину Т – промежуток времени между двумя появлениями события. По смыслу . Определим для нее функцию распределения:

Вероятность противоположного события ) равна вероятности того, что в промежутке времени (0,t) не наступит ни одно событие потока, т.е.

.

Следовательно, вероятность искомого события

при

Определение. Положительная случайная величина 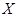имеет показательное распределение с параметром , если ее функция распределения задается формулой

для , для .

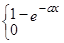
Плотность распределения находится по общему правилу

для .

Параметр а в ряде областей именуется «отношением риска».

Числовые характеристики: .

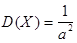Области применения.

Укажем две области.

1. Задачи, связанные с данными типа «времени жизни». В медико-биологических исследованиях под этим термином может подразумеваться продолжительность жизни больных при клинических исследованиях, в технике – продолжительность безотказной работы устройств, в психологии –время, затрачиваемое испытуемыми на выполнение тестовых задач и т.д..

2. Задачи массового обслуживания. Интервалы между вызовами «скорой помощи», телефонными звонками или обращением клиентов и т.д., описываются показательным распределением. Оно широко используется в теории надежности для описания распределения времени безотказной работы прибора или системы, если интенсивность отказа можно считать постоянной; длительности ремонта или другого вида обслуживания.

Пользуясь показательным распределением можно определить вероятность того, что время надежной работы не выйдет из заданного интервала .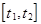

.

Задавшись вероятностью , можно определить время надежной работы, гарантированной с этой вероятностью, так как

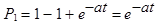и .

Пример 1. Пусть в результате наблюдений за работой системы в течение 100 ч зарегистрировано 5 отказов.

Определить:

1. Функцию надежности системы, т.е. что система будет работать без отказа.

2. Вероятность безотказной работы в течение 50 ч.

3. Время безотказной работы, гарантированное с вероятностью .

Решение. Из условия задачи известно, что t = 100, n = 5, a = 5:100 = 0,05 отказа в 1 час.

1. Функция надежности: .

2. .

3. .

Пример 2. Среднее время обслуживания покупателя 20 мин. Чему равна вероятность простоя в очереди от 20 до 40 минут?

Решение. Из условия задачи известно, что = 20 мин. Следовательно, 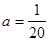. Искомая вероятность

.

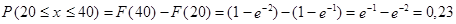3.4.8. Связь между некоторыми распределениями.

Случайная величина

Дискретная Непрерывная

Распределения Распределения

Биноми-альное	Пуассона	Гипергео-метрическое	Равномерное	Нормальное	Показательное

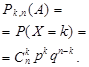
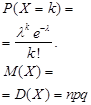
Некоторые из рассмотренных распределений при больших n и некоторых дополнительных условиях сходятся к другим типам распределений. Например, биноминальное распределение с параметрами n и p может быть аппроксимировано нормальным распределением с и , если выполняются условия npq > 5 и . При условии npq > 25 эту аппроксимацию можно применять независимо от значения p. При условии, что р < 0,1 и n велико биноминальное распределение может быть аппроксимировано распределением Пуассона. Распределение Пуассона может быть аппроксимировано нормальным распределением с , если . Когда , но 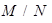и n остаются фиксированными, то гипергеометрическое распределение сходится к биномиальному. При малых р, больших n и гипергеометрическое распределение может аппроксимироваться распределением Пуассона.

Вопросы для самопроверки.

1. Что называется случайной величиной? Дайте определения дискретной и непрерывной случайных величин и приведите примеры такого рода величин.

2. Что называется распределением вероятностей дискретной случайной величины X и каким образом можно задать это распределение?

3. Дайте определение функции распределения и укажите ее свойства.

4. Дайте определение плотности распределения вероятностей и укажите ее свойства.

5. Укажите формулы для вычисления вероятности попадания случайной величины в заданный интервал.

6. Что называется математическим ожиданием случайной величины и каковы его свойства?

7. Что называется дисперсией случайной величины и каковы ее свойства?

8. Случайную величину X умножили на постоянную величину C. Как при этом изменится математическое ожидание, дисперсия и среднее квадратическое отклонение?

9. Дайте определение начального и центрального моментов порядка K. Какими моментами являются математическое ожидание и дисперсия?

10. Укажите числовые характеристики, описывающие форму распределения.

11. Какое распределение называется биномиальным? При каких условиях оно возникает?

12. Какое распределение называется распределением Пуассона и каковы условия его возникновения?

13. Написать формулу плотности нормального распределения и объяснить смысл входящих в нее параметров.

14. Написать формулу для вероятности попадания нормально распределенной случайной величины в заданный интервал [ ].

15. Как нужно преобразовать нормально распределенную случайную величину X , чтобы получить нормально распределенную величину Y ?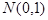

16. В чем состоит правило “трех сигм”? Каково его практическое применение?

Задачи.

3.1. Завод отправил на базу 100000 керамических изделий. Вероятность того, что изделие в пути разобьется, равна 0,00006. Составить закон распределения числа поврежденных изделий, указав первые 4 члена. Найти математическое ожидание и дисперсию этой случайной величины.

3.2. Два студента сдают 2 зачета. Вероятность того, что первый студент сдаст любой из зачетов равна 0,9, а второй – 0,8. Составить закон распределения общего числа сданных зачетов.

3.3. Вероятность того, что пассажир опоздает к отправлению поезда, равна 0,002.

а) Найти вероятность того, что 5 человек среди 1000 пассажиров некоего поезда опоздали;

б) составить первые три члена закона распределения числа опоздавших;

в) найти математическое ожидание и дисперсию этой случайной величины.

3.4. При некотором технологическом процессе брак составляет в среднем 3%. Составить закон распределения числа стандартных изделий среди взятых наудачу 5 изделий этого производства.

3.5. Вероятность того, что любой абонент позвонит на коммутатор в течение часа, равна 0,005. Телефонная станция обслуживает 600 абонентов. Найти вероятность того, что в течение часа позвонит пять абонентов.

3.6. В радиоаппаратуре за 10000 ч. непрерывной работы происходит замена десяти ламп. Найти вероятность выхода из строя радиоаппаратуры из-за выхода из строя ламп за 100 ч. непрерывной работы.

3.7. Вероятность того, что изделие не выдержит испытания, равна 0,0004. Найти вероятность того, что из 1000 изделий не выдержит испытаний не менее двух.

3.8. На шоссе установлен контрольный пункт для проверки технического состояния автомобилей. Найти математическое ожидание и среднее квадратическое отклонение времени ожидания машины контролером, если поток машин простейший и время (в часах) между прохождением машин через контрольный пункт распределено по показательному закону с параметром a = 10.

3.9. Для телефонной станции в интервале от 10 до 11 часов дня средняя интенсивность поступающих вызовов в стационарном режиме равна четырем вызовам в минуту. Найти вероятность поступления не более чем трех вызовов в интервале между ровно десятью и десятью и одной минутой часов.

3.10. Руководитель фирмы решил проверить работу своих служащих и дал указание сообщать ему каждый день, сколько заказов в этот день не было выполнено вовремя. Через 120 дней он обнаружил, что в среднем ежедневно не выполнялось шесть заказов. Обозначим через X число заказов, не выполненных в срок, и будем считать, что X = 0,1,2... Предположим также, что Х является случайной величиной, распределенной по закону Пуассона. Какова вероятность того, что в какой-то день не будет выполнено 6 или более заказов?

3.11. Функция распределения годовых доходов лиц, облагаемых налогом, построенная по многолетним статистическим данным, имеет вид:

, если и F (x) = 0, если x < ,

где > 0, > 0 – известные параметры. Определить плотность распределения и критический размер годового дохода, который для случайно выбранного налогоплательщика может быть превзойден с вероятностью 0,5.

3.12. Среднее время обслуживания пациента врачом 12 минут. Чему равна вероятность ожидания в очереди пациентом от 24 до 36 минут?

3.13. Пусть известно, что вес рыбы (в кг) распределен нормально N (2; 0,4). Определить (не прибегая к помощи таблиц) вероятность того, что вес выловленной рыбы будет: а) меньше 0,09 кг; б) больше 4 кг.

3.14. Средний процент выполнения плана некоторыми предприятиями составляет 102%, среднее квадратическое отклонение 9%. Полагая, что выполнение плана этой группой предприятий подчиняется нормальному закону, определить процент предприятий: а) не выполняющих план; б) выполняющих план от 101% до 115%.

3.15. Найти плотность вероятности и функцию распределения времени ожидания поезда метрополитена, зная, что оно равномерно распределено в интервале (0;3)мин. Вычислить математическое ожидание и дисперсию этой случайной величины.

3.16. Время ожидания троллейбуса пассажиром распределено равномерно с М (X)=3 мин. и D (X)=3 мин .

а) Найти плотность распределения и функцию распределения времени ожидания.

б) Найти вероятность того, что время ожидания не превысит 4 минуты

Date: 2016-07-25; view: 1503; Нарушение авторских прав