
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Характеристики формы распределения (асимметрия и эксцесс).
|
|
В отличие от начальных моментов, центральные моменты не меняются при прибавлении к случайной величине постоянного слагаемого, т.е. они не зависят от выбора начала отсчета в шкале измерения случайной величины. Но от выбранной единицы измерения зависимость остается: если, скажем, случайную величину начать измерять не в рублях, а в тысячах рублей, то значения центральных моментов тоже изменятся. Чтобы устранить подобное явление, моменты тем или иным способом нормируют, например, делят их на соответствующие степени среднего квадратического отклонения  . В результате получается безразмерная величина, не зависящая от выбора начала отсчета и единицы измерения исходной случайной величины.
. В результате получается безразмерная величина, не зависящая от выбора начала отсчета и единицы измерения исходной случайной величины.
Чаще всего из нормированных моментов используется асимметрия и эксцесс – соответственно третий и четвертый нормированные центральные моменты. Для случайной величины Х коэффициент асимметрии 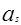 («скошенности» распределения) вычисляется по формуле:
(«скошенности» распределения) вычисляется по формуле:
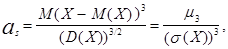
а коэффициент эксцесса 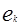 («островершинности» распределения) вычисляется по формуле
(«островершинности» распределения) вычисляется по формуле
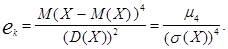
Принято считать, что асимметрия характеризует симметричность распределения случайной величины, а эксцесс – степень выраженности «хвостов» распределения, т.е. частоту появления удаленных от среднего значений.
Для симметричного распределения 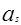 = 0.
= 0.
Если 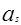 > 0, то имеет место правосторонняя асимметрия, т.е. распределение имеет более длинную часть справа от математического ожидания (рис. а), если
> 0, то имеет место правосторонняя асимметрия, т.е. распределение имеет более длинную часть справа от математического ожидания (рис. а), если 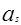 < 0, то имеет место левосторонняя асимметрия, т.е. распределение имеет более длинную часть слева от математического ожидания (рис. б).
< 0, то имеет место левосторонняя асимметрия, т.е. распределение имеет более длинную часть слева от математического ожидания (рис. б).
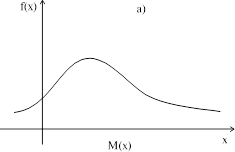
|

|
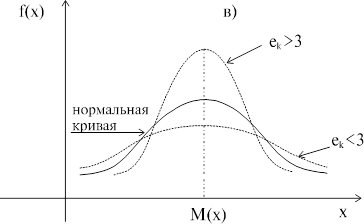
При оценке «островершинности» распределения в качестве эталонного выбирается нормальное распределение, для которого 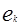 = 3. Если
= 3. Если 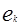 – 3 > 0, то распределение имеет более острую, при
– 3 > 0, то распределение имеет более острую, при 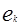 – 3 < 0 более пологую вершину, чем нормальное (см. рис. в)
– 3 < 0 более пологую вершину, чем нормальное (см. рис. в)
|
Квантили.
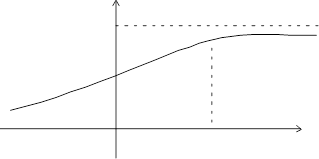
Для случайных величин, принимающих вещественное значение, часто используются такие характеристики, как квантили.
|
Функция распределения случайной величины любой точке 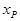 ставит в соответствие вероятность P = F (
ставит в соответствие вероятность P = F (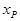 ) = P (X <
) = P (X < 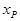 )
)
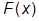
|
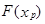
|
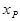
|
| Х |
Иногда возникает обратная задача: по заданному значению вероятности p найти такое значение 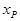 , чтобы выполнялось равенство F (
, чтобы выполнялось равенство F (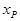 ) = p.
) = p.
Определение. Квантилью 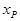 случайной величины Х, имеющей функцию распределения F (x), называется решение
случайной величины Х, имеющей функцию распределения F (x), называется решение 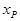 уравнения F (
уравнения F (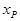 ) = p,
) = p,
0 < p < 1.
Величину 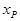 часто называют р – квантилью или квантилью уровня р распределения F (x). Среди квантилей чаще всего используются медиана и квартили распределения.
часто называют р – квантилью или квантилью уровня р распределения F (x). Среди квантилей чаще всего используются медиана и квартили распределения.
Медианой называется квантиль, соответствующая значению 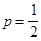 . Нижней квартилью называется квантиль, соответствующая значению
. Нижней квартилью называется квантиль, соответствующая значению 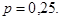 Верхней квартилью называется квантиль, соответствующая значению
Верхней квартилью называется квантиль, соответствующая значению 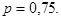
 В описательной статистике нередко используются децили, т.е. квантили уровней 0,1; 0,2; 0,3;...; 0,9. Значения децилей позволяют неплохо представить поведение графика y = F (x) в целом.
В описательной статистике нередко используются децили, т.е. квантили уровней 0,1; 0,2; 0,3;...; 0,9. Значения децилей позволяют неплохо представить поведение графика y = F (x) в целом.
Отметим, что уравнение F (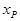 ) = p, определяющее р – квантили, для некоторых значений р может не иметь решений или иметь неединственное решение. Для соответствующей случайной величины это означает, что некоторые р – квантили не существуют, а некоторые определены неоднозначно.
) = p, определяющее р – квантили, для некоторых значений р может не иметь решений или иметь неединственное решение. Для соответствующей случайной величины это означает, что некоторые р – квантили не существуют, а некоторые определены неоднозначно.
Критической точкой порядка р (симметричной критической точкой величины р) распределения непрерывной случайной величины Х называется действительное число 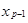 , удовлетворяющее уравнению
, удовлетворяющее уравнению
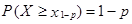 .
.
Квантиль и критическая точка одного и того же распределения связаны соотношением
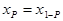
Date: 2016-07-25; view: 502; Нарушение авторских прав