Распределение Пуассона.

Рассмотрим наиболее типичную ситуацию, в которой возникает распределение Пуассона. Пусть событие А появляется некоторое число раз в фиксированном участке пространства (интервале, площади, объеме) или промежутке времени с постоянной интенсивностью. Для определенности рассмотрим последовательное появление событий во времени, называемое потоком событий. Графически поток событий можно иллюстрировать множеством точек, расположенных на оси времени.

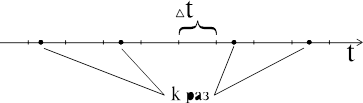
Это может быть поток вызовов в сфере обслуживания (ремонт бытовой техники, вызов скорой помощи и др.), поток вызовов на АТС, отказ в работе некоторых частей системы, радиоактивный распад, куски ткани или металлические листы и число дефектов на каждом из них и др. Наиболее полезным распределение Пуассона оказывается в тех задачах, где требуется определить лишь число положительных исходов («успехов»).

Представим себе булку с изюмом, разделенную на маленькие кусочки равной величины. Вследствие случайного распределения изюминок нельзя ожидать, что все кусочки будут содержать их одинаковое число. Когда среднее число 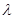изюминок, содержащееся в этих кусочках, известно, тогда распределение Пуассона задает вероятность того, что любой взятый кусочек содержит X = k (k = 0,1,2,...,)число изюминок.

Иначе говоря, распределение Пуассона определяет, какая часть 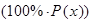длинной серии кусочков будет содержать равное 0, или 1, или 2, или и т.д. число изюминок.

Сделаем следующие предположения.

1. Вероятность появления некоторого числа событий в данном промежутке времени зависит только от длины этого промежутка, а не от его положения на временной оси. Это свойство стационарности.

2. Появление более одного события в достаточно малом промежутке времени 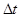практически невозможно, т.е. условная вероятность появления в этом же интервале другого события стремится к нулю при 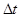® 0. Это свойство ординарности.

3. Вероятность появления данного числа событий на фиксированном промежутке времени не зависит от числа событий, появляющихся в другие промежутки времени. Это свойство отсутствия последействия.

Поток событий, удовлетворяющий перечисленным предложениям, называется простейшим.

Рассмотрим достаточно малый промежуток времени 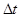. На основании свойства 2 событие может появиться на этом промежутке один раз или совсем не появиться. Обозначим вероятность появления события через р, а непоявления – через q = 1 -p. Вероятность р постоянна (свойство 3) и зависит только от величины 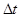(свойство 1). Математическое ожидание числа появлений события в промежутке 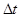будет равно 0× q + 1× p = p. Тогда среднее число появления событий в единицу времени называется интенсивностью потока и обозначается через a, т.е. a = .

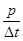Рассмотрим конечный отрезок времени t и разделим его на n частей 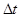= 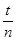. Появления событий в каждом из этих промежутков независимы (свойство 2). Определим вероятность 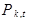того, что в отрезке времени t при постоянной интенсивности потока а событие появится ровно X = k раз и не появится n – k. Так как событие может в каждом из n промежутков 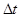появиться не более чем 1 раз, то для появления его k раз на отрезке длительностью t оно должно появиться в любых k промежутках из общего числа n. Всего таких комбинаций , а вероятность каждой равна 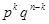. Следовательно, по теореме сложения вероятностей получим для искомой вероятности 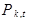известную формулу Бернулли

» .

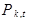Это равенство записано как приближенное, так как исходной посылкой при его выводе послужило свойство 2, выполняемое тем точнее, чем меньше 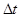. Для получения точного равенства перейдем к пределу при 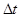® 0 или, что то же, n ® 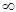. Получим после замены

P = a 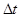= 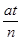и q = 1 – .

= = .

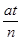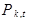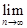
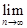
Введем новый параметр 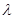= at, означающий среднее число появлений события в отрезке t. После несложных преобразований и переходу к пределу в сомножителях получим.

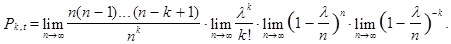
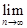
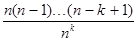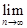
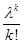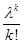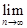
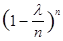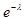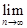
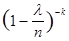= 1, = ,

= , = 1.

Окончательно получим

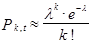, k = 0, 1, 2,...

е = 2,718... –основание натурального логарифма.

Определение. Случайная величина Х, которая принимает только целые, положительные значения 0, 1, 2,... имеет закон распределения Пуассона с параметром 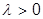, если

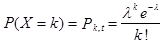для k = 0, 1, 2,...

Распределение Пуассона было предложено французским математиком С.Д. Пуассоном (1781-1840 гг). Оно используется для решения задач исчисления вероятностей относительно редких, случайных взаимно независимых событий в единицу времени, длины, площади и объема.

Для случая, когда а) 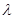– велико и б) k = 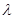, справедлива формула Стирлинга:

.

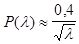Для расчета последующих значений используется рекуррентная формула

P (k + 1) = 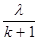P (k).

Пример 1. Чему равна вероятность того, что из 1000 человек в данный день родились: а) ни одного, б) один, в) два, г) три человека?

Решение. Так как p = 1/365, то q = 1 – 1/365 = 364/365» 1.

Тогда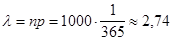

а) ,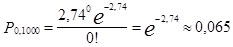

б) ,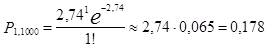

в) ,

г) .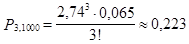

Следовательно, если имеются выборки из 1000 человек, то среднее число человек, которые родились в определенный день, соответственно будут равны 65; 178; 244; 223.

Пример 2. Определить значение 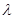, при котором с вероятностью Р событие появилось хотя бы один раз.

Решение. Событие А = {появиться хотя бы один раз} и 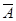= {не появиться ни одного раза}. Следовательно .

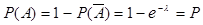Отсюда 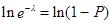и .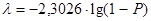

Например, для Р = 0,5 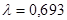, для Р = 0,95 .

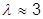Пример 3. На ткацких станках, обслуживаемых одной ткачихой, в течение часа происходит 90 обрывов нити. Найти вероятность того, что за 4 минуты произойдет хотя бы один обрыв нити.

Решение. По условию t = 4 мин. и среднее число обрывов за одну минуту 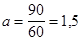, откуда 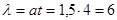. Требуемая вероятность равна .

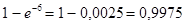Свойства. Математическое ожидание и дисперсия случайной величины, имеющей распределение Пуассона с параметром 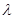, равны:

M (X) = D (X) = .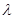

Эти выражения получаются прямыми вычислениями:

.

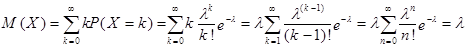Здесь была осуществлена замена n = k – 1 и использован тот факт, что .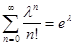

.

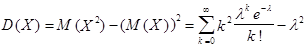Выполнив преобразования, аналогичные использованным при выводе М (X), получим

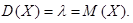
Распределение Пуассона используется для аппроксимации биноминального распределения при больших n

При изучении биноминального распределения указывалось на целесообразность асимптотических формул, облегчающих вычисление вероятностей для больших значений n (формулы Муавра-Лапласа). При выводе формулы распределения Пуассона было получено

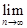
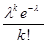= , ãäå 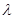= at и p = = .

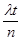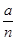Таким образом, биноминальное распределение при n ® 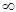стремится к распределению Пуассона с параметром 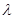. Так как параметр 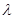– постоянное число (среднее число появления события), то с ростом n p = 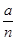® 0, т.е. предельное равенство предполагает неограниченное уменьшение р.

Переходя от предельного равенства к приближенному, при конечном n получим асимптотическую формулу Пуассона для биноминального распределения .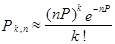

Строго говоря, предпосылка о постоянстве 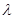, лежащая в основе вывода закона Пуассона (откуда следует переменная вероятность p = 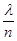), противоречит исходным условиям биноминального распределения (p = const). Однако приближенное равенство дает достаточно точные результаты при 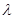непостоянном. Важно лишь сохранить условие малости р и достаточно большего п так, чтобы произведение пр было невелико (например, пр < 10).

Пример. В некоторой области в среднем один из 2000 домов ежегодно сгорает от пожара. Если в области имеется 4000 домов, то чему равна вероятность того, что в течение года случится ровно 5 пожаров?

Решение. По условию задачи , .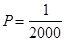

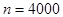Тогда 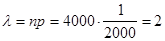и .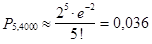

Date: 2016-07-25; view: 306; Нарушение авторских прав