
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Модуль 11. Модели стационарных и нестационарных временных рядов
|
|
Комплексная цель модуля 11:
Сформировать основы знаний о стационарных и нестационарных временных рядах, об основных подходах к распознаванию стационарности временных рядов.
Проектное задание к модулю 11:
1. Сформулируйте условия, при которых временной ряд x(t) можно называть нестационарным однородным.
2. Ответьте на вопрос, какой вид имеет процесс смешанного типа и что такое «белый шум».
3. Какой вид имеет общий линейный процесс, если он описывается классической линейной моделью множественной регрессии?
4. Какие факторы всегда участвуют в процессе формирования значений временного ряда?
Тест рубежного контроля к модулю 11
11. Тест содержит 6 заданий, на выполнение которых отводится 3 минуты. Выберите наиболее правильный, по Вашему мнению, вариант ответа и отметьте его любым значком в бланке ответов.
| 1 Стохастическим процессом называется | |||
набор случайных переменных X(t), где 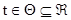 (вещественные числа); (вещественные числа);
| набор детерминированных переменных X(t); | ||
набор детерминированных и случайных переменных X(t), где 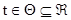 (вещественные числа); (вещественные числа);
| набор случайных переменных X(t), где 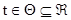 (детерминированные переменные). (детерминированные переменные).
| ||
| 2 Стохастический процесс Xt называется стационарным в сильном смысле, если | |||
совместное распределение вероятностей всех переменных 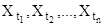 точно то же самое, что и для переменных точно то же самое, что и для переменных  ; ;
| совместное распределение вероятностей некоторых из переменных 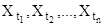 точно то же самое, что и для некоторых из переменных точно то же самое, что и для некоторых из переменных  ; ;
| ||
совместное распределение вероятностей всех переменных 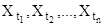 отличается от распределения вероятностей для переменных отличается от распределения вероятностей для переменных  ; ;
| распределение вероятностей одной переменной в ряду переменных 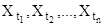 точно то же самое, что и для переменных точно то же самое, что и для переменных  . .
| ||
| 3 Под стационарным процессом в слабом смысле понимается стохастический процесс, для которого | |||
| среднее и дисперсия независимо от рассматриваемого периода времени имеют постоянное значение, а автоковариация зависит только от длины лага между рассматриваемыми переменными; | дисперсия независимо от рассматриваемого периода времени имеет постоянное значение, а автоковариация зависит только от длины лага между рассматриваемыми переменными; | ||
| среднее независимо от рассматриваемого периода времени имеет постоянное значение, а автоковариация зависит только от длины лага между рассматриваемыми переменными; | автоковариация зависит только от длины лага между рассматриваемыми переменными. | ||
| 4 Стационарность временного ряда означает отсутствие: | |||
| тренда, систематических изменений дисперсии; строго периодичных флуктуации; систематически изменяющихся взаимозависимостей между элементами временного ряда; | тренда и систематически изменяющихся взаимозависимостей между элементами временного ряда; | ||
| систематических изменений дисперсии; строго периодичных флуктуации; систематически изменяющихся взаимозависимостей между элементами временного ряда; | тренда, систематических изменений дисперсии. | ||
| 5 Эргодичность – это: | |||
поведение большого класса стационарных процессов, когда арифметическое среднее со временем сходится к математическому ожиданию 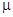 ; ;
| поведение малого класса нестационарных процессов, когда арифметическое среднее со временем сходится к математическому ожиданию 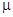 ; ;
| ||
поведение большого класса стационарных процессов, когда геометрическое среднее со временем сходится к математическому ожиданию 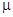 ; ;
| поведение большого класса нестационарных процессов, когда арифметическое среднее со временем сходится к математическому ожиданию 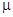 . .
| ||
| 6 «Белым шумом» называется: | |||
| чисто случайный процесс, т.е. ряд независимых, одинаково распределенных случайных величин at | детерминированный процесс, т.е. ряд независимых, одинаково распределенных величин at | ||
| чисто случайный процесс, т.е. ряд зависимых, одинаково распределенных случайных величин at | чисто случайный процесс, т.е. ряд независимых, различно распределенных случайных величин at. |
Бланк ответов
| № | ||||||
| 1) | ||||||
| 2) | ||||||
| 3) | ||||||
| 4) | ||||||
| 5) | ||||||
| 6) |
МОДУЛЬ 12. ПРИКЛАДНАЯ ЭКОНОМЕТРИКА: МОДЕЛЬ ЦЕНООБРАЗОВАНИЯ НА ОСНОВНОЙ КАПИТАЛ (ЦОК)
Комплексная цель модуля 12:
сформировать практические навыки использования линейных моделей парной регрессии в области постановки и решения экономических задач.
Проектное задание к модулю 12:
1. Определите задачи, решаемые эконометрикой в различных сферах экономики.
2. Ответьте на вопрос, какую информацию необходимо учитывать при проведении эконометрического исследования в области ценообразования на основной капитал и как можно обосновать необходимость диверсификации портфеля ценных бумаг эконометрическими методами.
3. Обоснуйте эндогенные и экзогенные переменные регрессионного уравнения прогнозирования прибылей по альтернативным ценным бумагам.
4. Приведите пример стратегии сочетания рискованного портфеля ценных бумаг с безрисковыми ценными бумагами для получения максимальной прибыли.
Тест рубежного контроля к модулю 12
12. Тест содержит 6 заданий, на выполнение которых отводится 3 минуты. Выберите наиболее правильный, по Вашему мнению, вариант ответа и отметьте его любым значком в бланке ответов.
| 1. Нобелевские премии по экономике за достижения с использованием эконометрического инструментария получили | |||
| Ян Тильберген, Рагнар Фриш, Лоуренс Клейн, Трюгве Хаавельмо, Джеймс Хекман и Дэниель Мак-Фадден; | Ян Тильберген, Рагнар Фриш, Василий Леонтьев, Джеймс Хекман и Дэниель Мак-Фадден; | ||
| Рагнар Фриш, Лоуренс Клейн, Трюгве Хаавельмо, Джеймс Хекман и Леонид Канторович; | Ян Тильберген, Рагнар Фриш, Лоуренс Клейн, Трюгве Хаавельмо и Дэниель Мак-Фадден. | ||
| 2. Ожидаемую (ex ante)норму прибыли от капиталовложений можно определить следующим образом: | |||
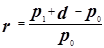
| 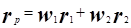
| ||

| 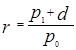
| ||
| 3 Риск,связанный с возможными капиталовложениями, обычно характеризуется | |||
| нормальным распределением возможных прибылей и измеряется дисперсией; | нормальным распределением возможных прибылей и измеряется стандартным отклонением σ; | ||
| логнормальным распределением возможных прибылей и измеряется стандартным отклонением σ; | бета-распределением возможных прибылей и измеряется стандартным отклонением σ. | ||
| 4 Компенсация (премия) за риск по j-йценной бумаге может быть определена как | |||
| превышение прибыли над свободной от риска нормой прибыли; | превышение свободной от риска нормы прибыли над ожидаемой прибылью, | ||
| превышение прибыли над связанной с риском нормой прибыли; | равенство прибыли свободной от риска норме прибыли. | ||
| 5 Предельная дисперсия – это: | |||
| изменение в дисперсии всего портфеля ценных бумаг в результате небольших изменений во вкладах k;она зависит от ковариации между прибылями от актива k и портфелем ценных бумаг. | изменение в дисперсии всего портфеля ценных бумаг в результате больших изменений во вкладах k; | ||
| изменение в дисперсии отдельных ценных бумаг в портфеле в результате небольших изменений во вкладах k;она зависит от ковариации между прибылями от актива k и портфелем ценных бумаг. | изменение в математическом ожидании всего портфеля ценных бумаг в результате небольших изменений во вкладах k;она зависит от вариации прибылей от актива k. | ||
6 Линейное соотношение между прибылью  и риском портфеля ценных бумаг и риском портфеля ценных бумаг 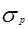 имеет вид: имеет вид:
| |||
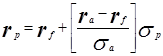
| 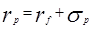
| ||
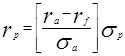
| 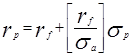
|
Бланк ответов
| № | ||||||
| 1) | ||||||
| 2) | ||||||
| 3) | ||||||
| 4) | ||||||
| 5) | ||||||
| 6) |
Date: 2016-07-22; view: 394; Нарушение авторских прав