Трение во вращательных парах

Вращательная кинематическая пара образуется цапфой (опорной частью вала) и охватывающим её подшипником.

Для того чтобы цапфа, находящаяся под действием нескольких приложенных к ней сил, могла вращаться, необходимо, чтобы равнодействующая Р этих сил (рис. 16.10) создавала момент не меньший момента силы трения.

Рис. 16.10

Разложив силу Р на нормальную Рⁿ и тангенциальную Р ^t составляющие и обозначив через: r плечо действия силы Р относительно оси вращения цапфы; R – радиус цапфы; l - угол между линией действия силы Р и радиусом, проведённым в точку приложения силы P, получим:

момент, вращающий цапфу, равен

;

момент силы F трения равен

.

Для возможности движения необходимо соблюдение условия

,

откуда

,

и поэтому

.

Следовательно, момент силы Р не может вращать цапфы, если линия действия силы Р проходит внутри круга с радиусом .

Такой круг получил название – круга трения.

Трение в пятах (трение верчения)

Трение в пятах имеет место на поверхности соприкосновения двух прижатых одно к другому тел, вращающихся одно относительно другого вокруг нормали к поверхности соприкосновения (рис. 16.11, а).

Рис. 16.11

При учете сопротивления, оказываемого силами трения моменту, вращающему одно тело относительно другого, приходится определять равнодействующий момент сил трения, заменяя элементарные силы трения на всей поверхности трения равнодействующей силой, приложенной на окружности с радиусом R. Определим величину радиуса R, предположив, что поверхность трения представляет собой кольцевую площадь с внешним радиусом r ₁ и внутренним радиусом r ₂ и что вращение происходит вокруг общего центра окружностей (рис. 16.11, б).

Полная сила трения скольжения равна:

,

где р – давление на поверхности трения, т.е. сила, приходящаяся на единицу поверхности трения; - площадь поверхности соприкосновения.

Момент полной силы трения

,

где R – радиус окружности, на которой приложена равнодействующая элементарных сил трения.

Элементарная сила трения, распределённая по кольцу с площадью , равна

.

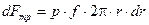Момент элементарной силы трения равен

.

Суммарный момент

.

Тогда приравнивая правые половины уравнений, получаем равенство

,

откуда

.

При r ₂ = 0, получаем .

Контрольные вопросы

44. Что такое трение, и от чего оно зависит.

45. Трение скольжения: сила, угол и конус трения.

46. Трение на горизонтальной плоскости.

47. Трение на наклонной плоскости.

48. Трение клинчатого ползуна, приведенный коэффициент трения.

49. Трение во вращательных парах.

50. Трение в пятах.

Лекция 17

Трение гибких тел. Трение качения. Коэффициент полезного действия механизмов: общие сведения, КПД при последовательном и параллельном соединении звеньев, КПД винтовой передачи.

Трение гибких тел

Рассмотрим идеально гибкое и нерастяжимое тело, т.е. тело, совершенно не деформирующееся под действием растягивающей силы и не оказывающее никакого сопротивления при его перегибе, которое огибает неподвижный цилиндр. Охват цилиндра происходит по дуге ab с центральным углом a (рис. 17.1). На тело действуют силы S ₁ и S ₂, для движения его по цилиндру с равномерной скоростью необходимо соблюдение условия

,

где F – сила трения между гибким телом и цилиндром.

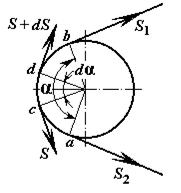
Рис. 17.1

Так как сила трения распределена на дуге ab соприкосновения гибкого тела с цилиндром, то натяжение гибкого тела от точки a набегания его на цилиндр до точки b сбегания его с цилиндра возрастает по некоторому закону от S ₂ до S ₁. В точке с бесконечно малой дуги cd натяжение достигает некоторой величины S, в точке d натяжение увеличивается до S + dS.

Бесконечно малая сила трения на дуге cd, обуславливающая увеличение натяжения на величину dS и поэтому равная dS, может быть выражена следующим образом:

,

где f – коэффициент трения; dRⁿ – бесконечно малая сила, нормальная к поверхности трения.

Величина силы dRⁿ создается проекциями натяжений S и S + dS на радиус, проведенный в середину дуги cd:

.

Так как и , как член высшего порядка малости, то

;

.

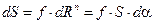Разделив, получаем

.

Интегрируя, а затем, дифференцируя, получаем

;

;

;

.

Зависимость между силой S ₁, движущей идеально гибкое и нерастяжимое тело, охватывающее цилиндр, и силой S ₂, сопротивляющейся движению была получена Л. Эйлером.

На основании формулы Эйлера сила трения на поверхности соприкосновения гибкого тела и охватываемого им цилиндра равна

.

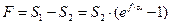Анализируя формулу, видим, что величина силы трения в значительной степени зависит и от коэффициента трения и от угла охвата: при f = 0,35 обмотав гибкое тело вокруг цилиндра на два полных оборота (a = 4p), силой 10 Н, можно уравновесить силу 800 Н.

Трение качения

При перекатывании одного тела, имеющего криволинейную поверхность, по другому телу с плоской или криволинейной поверхностью возникает сопротивление, которое называется трением второго рода или трением качения. Сопротивление перекатыванию зависит от упругих свойств материалов соприкасающихся тел, кривизны их поверхностей и величины нормальной силы, действующей между телами.

Пусть на плоскости лежит цилиндр, вес которого G (рис. 17.2, а). Так как цилиндр и плоскость не являются абсолютно твёрдыми телами, то в зоне их соприкосновения под действием силы G образуется некоторая площадка смятия АВ. Согласно теории упругости Герца, в зоне площадки смятия напряжения распределяются по эллиптическому закону. Равнодействующая этих напряжений Rⁿ будет равна по величине и противоположна по направлению силе G и действует по одной линии с нею.

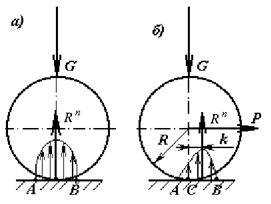
Рис. 17.2

Если цилиндр не будет находиться в статическом состоянии, то закон распределения напряжений изменится: на участке СВ контактной площадки напряжения будут больше, нежели на участке АС (рис. 17.2, б). Участок СВ называется зоной нарастающих деформаций, а участок АС – зоной исчезающих деформаций. Зона исчезающих деформаций является результатом гистерезиса, т.е. сохранения части деформаций и после того, как исчезла причина, вызвавшая эту деформацию.

Равнодействующая напряжений всей контактной площадки, равная внешней нагрузке G, будет смещена за вертикальную ось симметрии цилиндра на некоторую величину k. Эту величину называют коэффициентом трения качения.

Для перекатывания тела необходимо преодолеть момент трения равный:

.

Если на цилиндр действует внешняя сдвигающая горизонтальная сила Р, приложенная по центру цилиндра, то для преодоления момента трения необходимо приложить момент

,

откуда внешняя сдвигающая сила

.

Отношение k/R можно рассматривать как приведенный коэффициент трения .

Если между телами сцепление недостаточно, то возможно появление скольжения

., т.е. или .

Таким образом, при тело будет катиться без скольжения, в противном случае тело будет скользить без качения. При будет одинаковая возможность и качения и скольжения.

Date: 2016-07-18; view: 699; Нарушение авторских прав