
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Связь между бесконечно малыми и бесконечно большими величинами
|
|
Теорема: Если функция α(x) есть бесконечно малая величина при  (при
(при  ), то функция
), то функция  является бесконечно большой при
является бесконечно большой при  (при
(при  ). И обратно, если функция f(x) бесконечно большая при
). И обратно, если функция f(x) бесконечно большая при  (при
(при  ), то функция
), то функция  есть величина бесконечно малая при
есть величина бесконечно малая при  (при
(при  ).
).
Раскрытие неопределённостей.
Если при вычислении пределов получается отношение вида  или
или  , то сразу сказать чему равен предел нельзя. В этом случае говорят, что получена неопределённость вида
, то сразу сказать чему равен предел нельзя. В этом случае говорят, что получена неопределённость вида  или
или  . Для раскрытия таких неопределённостей можно разложить числитель и знаменатель дроби на множители, разделить числитель и знаменатель дроби на переменную в наибольшей степени или применить замечательные пределы. Раскрытие неопределённостей вида
. Для раскрытия таких неопределённостей можно разложить числитель и знаменатель дроби на множители, разделить числитель и знаменатель дроби на переменную в наибольшей степени или применить замечательные пределы. Раскрытие неопределённостей вида  сначала сводится к неопределённостям вида
сначала сводится к неопределённостям вида  или
или  .
.
Односторонние пределы
Определение: число А+ будем называть правым односторонним пределом функции f (x), если для любого, сколь угодно малого, e > 0 найдется положительное число δ, такое, что как только выполнено неравенство 0 < x – a < δ (a < x < a + δ), так сразу f (x) попадает в эпсилон-окрестность числа А+, т.е.: 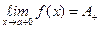
Т.о.Число А называется правым пределом функции f(x) в точке а, если  такое, что для каждого х, удовлетворяющего условию
такое, что для каждого х, удовлетворяющего условию 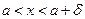 верно неравенство │
верно неравенство │ 
Обозначается: 
Аналогично определяется левый односторонний предел:  и в этом случае неравенство будет иметь вид: 0 < а – х < δ (a – δ < x < a).
и в этом случае неравенство будет иметь вид: 0 < а – х < δ (a – δ < x < a).
Число А называется левым пределом функции f(x) в точке а, если 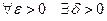 такое, что для каждого х, удовлетворяющего условию
такое, что для каждого х, удовлетворяющего условию  верно неравенство │
верно неравенство │ 
Обозначается: 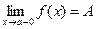
Eсли x® a и при этом x > a, то пишут x® a+0. Если, в частности, a=0, то вместо символа 0+0 пишут +0. Аналогично если x®a и при этом x<a, то пишут x®a-0. Числа  и
и 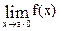 называются соответственно пределом справа и пределом слева функции f(x) в точке а. Для существования предела функции f(x) при x®a необходимо и достаточно, чтобы
называются соответственно пределом справа и пределом слева функции f(x) в точке а. Для существования предела функции f(x) при x®a необходимо и достаточно, чтобы  =
= 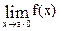 .
.
Непрерывность функции.
Определение 1. Функция  называется непрерывной в точке х0 если:
называется непрерывной в точке х0 если:
1. Эта функция определена в некоторой окрестности точки х0.
2. Существует конечный предел  при
при 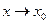 , т. е.
, т. е. 
3. 
Определение 2. Функция  называется непрерывной в точке х0, если она определена в этой точке и бесконечно малому приращению
называется непрерывной в точке х0, если она определена в этой точке и бесконечно малому приращению  аргумента х, соответствует бесконечно малое приращение функции
аргумента х, соответствует бесконечно малое приращение функции 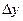 то есть
то есть 
Итак, функция f (x) называется непрерывной в точке а, если предел функции в этой точке равен значению функции в этой же точке, т.е.:

 |
Свойства функций непрерывных в точке.
Если функции  и
и 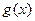 непрерывны в точке х0, то:
непрерывны в точке х0, то:
1. их сумма (разность) (f (x) + g (x)), (f (x) – g (x)) является функцией непрерывной в точке х0
2. их произведение (f (x) × g (x))является функцией непрерывной в точке х0
3. их частное  , при условии
, при условии 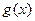 >0, является функцией непрерывной в точке х0
>0, является функцией непрерывной в точке х0
4. если функция  непрерывна в точке u0, а функция
непрерывна в точке u0, а функция 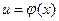 непрерывна в точке х0, то сложная функция
непрерывна в точке х0, то сложная функция  непрерывна в точке х0.
непрерывна в точке х0.
Определение: Функция  называется непрерывной на промежутке Х если она непрерывна в каждой точке этого промежутка.
называется непрерывной на промежутке Х если она непрерывна в каждой точке этого промежутка.
Теорема: всякая элементарная функция непрерывна в каждой точке своей области определения.
Определение: пусть функция y = f (x) определена на промежутке [a; b] и принимает значения на промежутке [α; β], и пусть на промежутке [α; β] определена функция z = z (y), тогда будем говорить, что на промежутке [a; b] определена сложная функция z = z (f (x)).
Пример: 
Теорема: если функция y = f (x) непрерывна в точке а, а функция z = z (f (x)) непрерывна в точке f (a), то сложная функция z = z (f (x)) будет непрерывной в точке а.
 |  |  | |||
Точки разрыва и их классификация
 |  |  | |||
Определение: Точка х0 называется точкой разрыва функции
 , если в данной точке х0 нарушается хотя бы одно условие непрерывности функции
, если в данной точке х0 нарушается хотя бы одно условие непрерывности функции  , а саму функцию
, а саму функцию  называют при этом разрывной.
называют при этом разрывной.
Точки разрыва подразделяются на точки разрыва первого и второго рода.
Точка х0 называется точкой разрыва первого рода функции  , если в этой точке существуют конечные, но неравные между собой односторонние пределы
, если в этой точке существуют конечные, но неравные между собой односторонние пределы  ;
;  .
.
Точка х0 называется точкой устранимого разрыва для функции  , если существует предел
, если существует предел  при
при 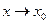 , а сама функция
, а сама функция  в точке х0 либо не определена, либо
в точке х0 либо не определена, либо  не равно пределу
не равно пределу  .
.
Разрыв можно устранить если функцию  доопределить в точке х0 или изменить её значение следующим образом (сделать равными)
доопределить в точке х0 или изменить её значение следующим образом (сделать равными)  .
.
Пусть х0 - точка разрыва первого рода, тогда скачком функции  в точке х0 называется разность односторонних пределов.
в точке х0 называется разность односторонних пределов.
Чтобы найти значение скачка надо от значения правого предела вычесть значение левого предела.
Точки устранимого разрыва и точки скачка являются точками разрыва 1-го рода.
Точка х0 называется точкой разрыва второго рода (точкой бесконечного разрыва)функции  если в этой точке не существует хотя бы один конечный односторонний предел слева или справа.
если в этой точке не существует хотя бы один конечный односторонний предел слева или справа.
Свойства функций непрерывных на отрезке.
Функция  называется непрерывной на отрезке [ a,b ] если она непрерывна на интервале (a,b) и, кроме того в точке a -непрерывна слева, а в точке b -справа.
называется непрерывной на отрезке [ a,b ] если она непрерывна на интервале (a,b) и, кроме того в точке a -непрерывна слева, а в точке b -справа.
Теорема Вейерштрасса: Если функция  непрерывна на отрезке [ a,b ], то на отрезке [ a,b ] она достигает своего наибольшего и наименьшего значения, то есть существуют такие точки х1 и х2
непрерывна на отрезке [ a,b ], то на отрезке [ a,b ] она достигает своего наибольшего и наименьшего значения, то есть существуют такие точки х1 и х2 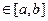 , что для всех x
, что для всех x 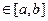 выполняются неравенства
выполняются неравенства  и
и  (x1 - максимум, x2 - минимум).
(x1 - максимум, x2 - минимум).
Пусть функция f (x) определена и непрерывна на замкнутом промежутке [a; b], тогда на этом промежутке она достигает свои наибольшее и наименьшее значения, т.е.:
 ; f (x1) = m; f (x2) = M.
; f (x1) = m; f (x2) = M.

Теорема Больцано-Коши: Если  непрерывна на отрезке [ a,b ] и на концах его принимает различные значения, то между точками a и b найдется точка с, такая что
непрерывна на отрезке [ a,b ] и на концах его принимает различные значения, то между точками a и b найдется точка с, такая что 
Пусть функция f (x) определена и непрерывна на замкнутом промежутке [a; b],
т.е.: f (x) Î C [a; b] и пусть на концах этого промежутка она принимает значения разных знаков (f (a) × f (b) < 0), тогда внутри промежутка [a; b] существует точка С, в которой функция обращается в ноль:
f (a) × f (b) < 0 Þ $ с Î (a; b): f (c)=0
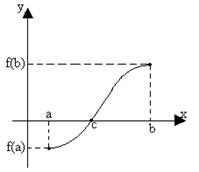 |
f (a) × f (b) < 0; f (c)=0
Таких точек (С) в принципе может быть несколько. Теорема Коши гарантирует, что есть хотя бы одна.
Замечание: на первой теореме Коши основан один из приближенных методов решения алгебраических уравнений, а именно метод половинного деления (дихатомии).
 |
Пусть нам известно, что не промежутке (a; b) уравнение f (x) = 0. в качестве первого приближенного значения корня берут середину этого отрезка:

Точность, с которой найден корень, равна половине ширины отрезка (a; b), обозначается δ.
2) на втором шаге выбирают в два раза меньший отрезок, на концах которого функция принимает значения разных знаков. Обозначают его границы a1; b1, и в качестве второго приближенного значения корня берут его середину: 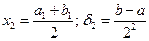
И так далее. На n-м шаге получим n-е приближенное значения корня:

Теорема Коши: Пусть  непрерывна на отрезке [ a,b ] и
непрерывна на отрезке [ a,b ] и  ,
,  , тогда найдется для любого числа С, заключенного между числами А и В, внутри отрезка АВ (
, тогда найдется для любого числа С, заключенного между числами А и В, внутри отрезка АВ ( ) такая точка С, что
) такая точка С, что 
 Если функция f (x) определена и непрерывна на замкнутом промежутке [a; b] и принимает на концах этого промежутка разные значения, т.е. f (a) ≠ f (b), то для любого числа γ между числами f (a) и f (b) найдется (внутри промежутка (a; b)) точка С, такая, что функция в этой точке равна γ, т.е.
Если функция f (x) определена и непрерывна на замкнутом промежутке [a; b] и принимает на концах этого промежутка разные значения, т.е. f (a) ≠ f (b), то для любого числа γ между числами f (a) и f (b) найдется (внутри промежутка (a; b)) точка С, такая, что функция в этой точке равна γ, т.е. 

Вторая теорема Коши является следствием первой теоремы Коши.
Следствие из теорем Коши и Вейерштрасса:
Если f (x) непрерывна на замкнутом отрезке [a; b], то ее значения сплошь заполняют некоторый замкнутый промежуток.
Замечание: графики непрерывных функций на координатной плоскости являются непрерывными кривыми, т.е. их можно нарисовать не отрывая карандаш от листа бумаги.
Лекция 8 Дифференциальное исчисление функции одной переменной ( Тема 3.2.)
План лекции
Определение производной её геометрический и физический смысл.
Производные элементарных функций.
Производная сложной функции, дифференциал функции.
Производные и дифференциалы высших порядков.
Исследование функций с помощью дифференциального исчисления.
Понятие производной
Определение. Производной функции  в точке
в точке 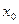 называется предел отношения приращения функции в этой точке к приращению аргумента при
называется предел отношения приращения функции в этой точке к приращению аргумента при  (при условии, что этот предел существует).
(при условии, что этот предел существует).
Производная обозначается  или
или 
Итак, по определению,  .
.
Нахождение производной называется дифференцированием функции.
Исходя из определения, составить, опираясь на рассуждения студентов, алгоритм отыскания производной.
Пусть функция у = f (x) определена в точке х0 и во всех точках, достаточно близких в точке х0, т.е. в некоторой окрестности точки х0. тогда выберем приращение аргумента ∆х такое, что х0 + ∆х не выходит за пределы этой окрестности. Тогда составим и вычислим предел отношения приращения функции к приращению аргумента при условии ∆х→ 0. Если этот предел имеет конечное значение, то он называется производной функции f (x) в точке х0 , т.е. 
Для производной используются также другие обозначения: 
Теорема: если функция у = f (x) имеет производную в точке х0 , то она непрерывна в этой точке (обратное утверждение в общем случае неверно).
Геометрический смысл производной функции f (x) в точке х0 состоит в том. Что она равна тангенсу угла наклона (т.е. угловому коэффициенту) касательной, проведенной в этой же точке.
Понятие производной впервые ввели: Ньютон, исходя из задач механики, и Лейбниц, исходя из геометрических построений, которые мы только что рассмотрели.
Уравнение касательной и нормали к кривой.
Касательная проходит через точку с координатами (х0; f(х0)) и имеет угловой коэффициент  , тогда получим следующее уравнение касательной:
, тогда получим следующее уравнение касательной:

Нормалью к кривой будем называть прямую линию, проходящую через точку касания перпендикулярно касательной (смотри рис.1).
Нормаль проходит через ту же самую точку с координатами (х0; f(х0)), угловой коэффициент нормали:  . Получим уравнение:
. Получим уравнение: 

Геометрический смысл производной.
Обозначим угол наклона секущей через β. Тогда:  .
.
Устремим ∆х к нулю, тогда секущая превратиться в касательную, проведенную к кривой в точке х0. угол наклона касательной обозначим через a.
Получим: 
 |  |
∆х→ 0

Пример Используя определение производной, найти производную функции  в точке
в точке  .Решение. Придавая аргументу
.Решение. Придавая аргументу  в точке
в точке 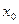 приращения
приращения  , найдем соответствующее приращение функции:
, найдем соответствующее приращение функции: 
Составим соотношение  .Найдем предел этого отношения при
.Найдем предел этого отношения при
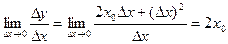
Следовательно, производная функции  в точке
в точке 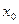 равна числу 2
равна числу 2 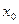 , что в принятых обозначениях можно записать так:
, что в принятых обозначениях можно записать так: 
Вычисление производных
Основные формулы дифференцирования:
1. 
| 2. 
| 3. 
|
4. 
| 5. 
| 6. 
|
7. 
| 8. 
| 9. 
|
10. 
| 11. 
| 12. 
|
13. 
| 14. 
| 15. 
|
Правила дифференцирования:1) 
2) 
3) 


4) 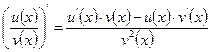
5) правило дифференцирования сложной функции:  , тогда:
, тогда:  . Производная сложной функции равна произведению производной внешней функции по ее аргументу на производную внутренней функции.
. Производная сложной функции равна произведению производной внешней функции по ее аргументу на производную внутренней функции.
Геометрически производная представляет собой угловой коэффициент касательной к графику функции y = f(x) в точке x, т. е. y / = tg a. Производная есть скорость изменения функции в точке x.
Пример Используя правила и формулы дифференцирования, найти производные функции: 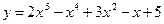 .
.
Решение:  .
.
Пример Используя правила и формулы дифференцирования, найти производные функции: 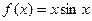
Решение. 
Производные высших порядков 
Пусть мы нашли для функции y=f(x) ее производную y ¢= f ¢(x). Производная от этой производной называется производной второго порядка функции f(x), или второй производной, и обозначается  .
.
Аналогично определяются и обозначаются:
производная третьего порядка -  ,
,
производная четвертого порядка - 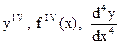
и вообще производная n-го порядка -  .
.
Понятие дифференциала
Пусть функция определена в точке х0 и некоторой ее окрестности.
Определение: дифференциалом независимой переменной х будем называть ее приращение (Δx = x – x0), dx = Δx – для независимой переменной.
Определение: функция f (x) называется дифференцируемой в точке х0, если ее приращение в этой точке  может быть представлено в виде:
может быть представлено в виде:  .
.  , где
, где 
Определение: дифференциалом функции f (x) называется главная линейная часть ее приращения, т.е. 
 ,
, 
 (1)
(1)

Положив в формуле (1)  , получаем
, получаем  , окончательно соотношение (1) принимает вид:
, окончательно соотношение (1) принимает вид: 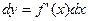 (2)
(2)
При достаточно малых  приращение функции приближенно равно ее дифференциалу
приращение функции приближенно равно ее дифференциалу  .
.
Пример Найти дифференциал функции  в точке x=2, причем сделать это двумя способами:
в точке x=2, причем сделать это двумя способами:
1) выделяя главную, линейную относительно  часть приращения функции
часть приращения функции 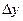 ;
;
2) по формуле (2).
Решение.
1)  отсюда
отсюда  ,
,
2) по формуле (2),  Следовательно, получаем
Следовательно, получаем  .
.
Пример Вычислить дифференциал функции  .
.
Решение. 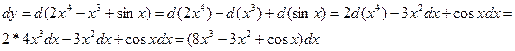
Date: 2016-07-18; view: 480; Нарушение авторских прав