Свойства обратных матриц

1) 2)

Вычисление обратной матрицы.

1. Обратную матрицу можно вычислить следующим образом:

.

Здесь верхний индекс Т обозначает операцию транспонирования матрицы – перемену местами строк и столбцов данной матрицы.

2. Нахождение обратной матрицы при помощи элементарных преобразований.

К исходной матрице справа приписывается единичная матрица того же порядка. Совершаются элементарные преобразования с целью получить на месте исходной матрицы единичную. Матрица, которая получится справа от нее и будет обратной к матрице А.

Пример

.

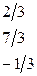
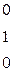
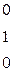
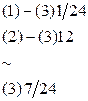
Лекция 3 Системы линейных алгебраических уравнений (СЛАУ)

( Тема 1.2.)

План лекции

Однородные и неоднородные системы уравнений.

Матрица коэффициентов и расширенная матрица системы.

Критерий совместности системы n-линейных уравнений с n-неизвестными (Теорема Кронекера-Капелли).

Методы решения систем линейных уравнений: метод Крамера, Гаусса и обратной матрицы.

Рассмотрим систему: (1)

Решением системы называется любая совокупность значений неизвестных ; ; …; , при подстановке которых все уравнения системы обращаются в тождества.

Матрица A= -матрица коэффициентов системы или матрица системы. -столбец свободных членов.

A*= -расширенная матрица системы.

Задача – найти решение системы.

Система, имеющая решение – совместна.

Система, не имеющая решения – несовместна.

Правило Крамера. Если определитель матрицы системы n уравнений с n неизвестными отличен от нуля (), то система имеет единственное решение, определяемое формулами:

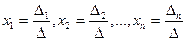() или .

Здесь - определитель, получаемый из путем замены i- го столбца на столбец свободных членов.

Для доказательства умножим первое уравнение системы (1) на А ₁₁, второе - на А ₂₁ и т.д. Последнее – на , затем сложим их все. Получим:

₁ (a₁₁ A₁₁ + a₂₁ A₂₁ + … + a_n1 A_n1 ) +

⁺ ₂ (a₁₂ A₂₁ + a₂₂ A₂₁ + … + a_n2 A_n1) + …+

+ _n (a_1n A₁₁ + a_2n A₂₁ + … + a_nn A_n1) =

=b₁ A₁₁ + b₂ A₂₁ + …+ b_n A_n1.

₁ * =b₁ A₁₁ + b₂ A₂₁ + …+ b_n A_n1.

При этом b₁ A₁₁ + b₂ A₂₁ + …+ b_n A_n1 - это определитель , разложенный по первому столбцу.

Аналогично получим ₂ * = ₂ и т.д. Откуда ₁ = , ₂ = , …, _n = .

Метод Гаусса

Решение системы линейных уравнений путем исключения неизвестных.

Элементарные преобразования системы уравнений – такие, которые приводят к получению эквивалентной системы уравнений, т. е. не изменяют систему. К ним относятся:

1) перемена местами двух уравнений системы.

2) умножение какого-либо уравнения системы на число

3) умножение какого-либо уравнения системы на любое число и прибавление его к другому уравнению.

Алгоритм Гаусса использует элементарные преобразования для получения системы уравнений, которая решается проще, чем исходная.

Пусть дана система m линейных алгебраических уравнений с n неизвестными:

(2)

Расширенная матрица системы имеет вид

.

При помощи элементарных преобразований расширенная матрица системы приводится к наиболее простому виду (ступенчатому), из которого непосредственно можно получить решение системы. При этом можно интуитивно совершать те или иные преобразования, имея цель получить в итоге нули слева и ниже главной диагонали. А можно использовать стандартный алгоритм, который заключается в так называемом прямом и обратном ходах.

Алгоритм метода Гаусса:

a) Переставляем уравнения системы так, чтобы .

b) Умножаем первое уравнение на и вычитаем из 2-го. Затем и вычитаем из 3-го и так далее. В результате такого преобразования переменная будет исключена из всех уравнений, кроме 1-го.

c) Если появились уравнения вида ,удаляем их из системы.

(Конец первого шага).

d) Второй шаг аналогичен первому, только (при ) второе уравнение умножают сначала на , потом (2) и так далее и вычитают его из 3-го,4-го,…, m-го уравнений. В результате исключаем из всех уравнений, кроме 1-го и 2-го.

e) На третьем шаге исключаем и так далее.

f) Через m шагов прямого хода система приводится к виду

Здесь (мы удалили тождества вида 0=0).

При система будет иметь треугольный вид.

Если на каком-либо этапе встретится уравнение вида:

, то система несовместна. Решение прекращается.

При (треугольная система) путём обратного хода вычисляется единственное решение.

При r<n система имеет вид трапеции. Неизвестные ,… - это главные неизвестные, … - свободные. Они могут принимать любые фиксированные значения. Придав свободным неизвестным некоторые фиксированные значения , начинаем обратный ход метода Гаусса. Получаем:

Общее решение: = = … = …

При различных наборах значений получаются различные частные решения системы.

Пример 1.

Составляем расширенную матрицу системы и совершаем прямой ход метода Гаусса:

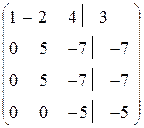
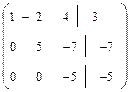
Обратный ход: решаем уравнения, начиная с последнего:

,

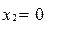
Пример 2.

Система имеет множество решений. Главные неизвестные - . Свободные неизвестные - 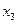, 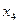- могут принимать любые значения.

Пример 3.

.

Последняя строка имеет вид

Уравнение не выполняется ни при каких х, следовательно,система несовместна.

Систему линейных алгебраических уравнений (nxn) можно записать в матричном виде: , , .

Тогда решением системы будет (если ) .

Пример:

,

.

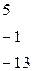
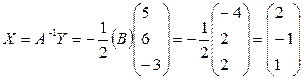Date: 2016-07-18; view: 362; Нарушение авторских прав