
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Определение узла дерева по его номеру
|
|
Идея данного подхода в том, чтобы заменить рекурсивные вызовы простым циклом, который выполнится столько раз, сколько узлов в дереве, образованном рекурсивными процедурами. Что именно будет делаться на каждом шаге, следует определить по номеру шага. Сопоставить номер шага и необходимые действия – задача не тривиальная и в каждом случае ее придется решать отдельно.
Например, пусть требуется выполнить k вложенных циклов по n шагов в каждом:
| for i1:= 0 to n-1 do for i2:= 0 to n-1 do for i3:= 0 to n-1 do … |
Если k заранее неизвестно, то написать их явным образом, как показано выше невозможно. Используя прием, продемонстрированный в разделе 6.5 можно получить требуемое количество вложенных циклов с помощью рекурсивной процедуры:
| procedure NestedCycles(Indexes: array of integer; n, k, depth: integer); var i: integer; begin if depth <= k then for i:=0 to n-1 do begin Indexes[depth]:= i; NestedCycles(Indexes, n, k, depth + 1); end else DoSomething(Indexes); end; |
Чтобы избавиться от рекурсии и свести все к одному циклу, обратим внимание, что если нумеровать шаги в системе счисления с основанием n, то каждый шаг имеет номер, состоящий из цифр i1, i2, i3, … или соответствующих значений из массива Indexes. То есть цифры соответствуют значениям счетчиков циклов. Номер шага в обычной десятичной системе счисления:
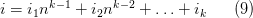
Всего шагов будет nk. Перебрав их номера в десятичной системе счисления и переведя каждый из них в систему с основанием n, получим значения индексов:
| M:= round(IntPower(n, k)); for i:= 0 to M-1 do begin Number:= i; for p:= 0 to k-1 do begin Indexes[k – p]:= Number mod n; Number:= Number div n; end; DoSomething(Indexes); end; |
Еще раз отметим, что метод не универсален и под каждую задачу придется придумывать что-то свое.
Еще один замечательный пример - вычисление по номеру шага перекладываний в задаче о Ханойских башнях смотрите тут: http://algolist.manual.ru/maths/combinat/hanoi.php
Контрольные вопросы
1. Определите, что сделают приведенные ниже рекурсивные процедуры и функции.
(а) Что напечатает приведенная ниже процедура при вызове Rec(4)?
| procedure Rec(a: integer); begin writeln(a); if a>0 then Rec(a-1); writeln(a); end; |
(б) Чему будет равно значение функции Nod(78, 26)?
| function Nod(a, b: integer): integer; begin if a > b then Nod:= Nod(a – b, b) else if b > a then Nod:= Nod(a, b – a) else Nod:= a; end; |
(в) Что будет напечатано приведенными ниже процедурами при вызове A(1)?
| procedure A(n: integer); procedure B(n: integer); procedure A(n: integer); begin writeln(n); B(n-1); end; procedure B(n: integer); begin writeln(n); if n < 5 then A(n+2); end; |
(г) Что напечатает нижеприведенная процедура при вызове BT(0, 1, 3)?
| procedure BT(x: real; D, MaxD: integer); begin if D = MaxD then writeln(x) else begin BT(x – 1, D + 1, MaxD); BT(x + 1, D + 1, MaxD); end; end; |
2. Уроборос – змей, пожирающий собственный хвост (рис. 14) в развернутом виде имеет длину L, диаметр около головы D, толщину брюшной стенки d. Определите, сколько хвоста он сможет в себя впихнуть и в сколько слоев после этого будет уложен хвост?
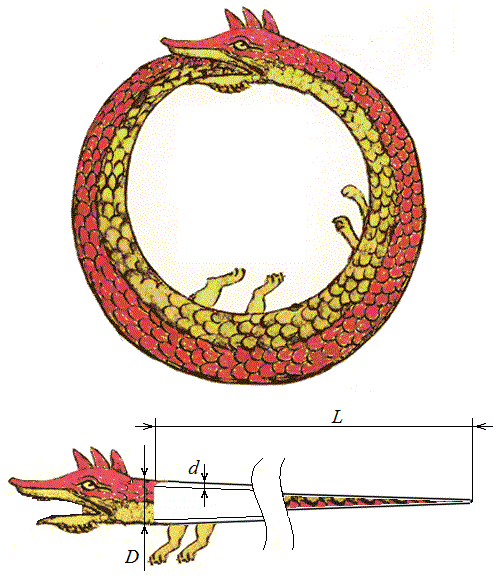
Рис. 14. Развернутый уроборос.
3. Для дерева на рис. 10а укажите последовательности посещения узлов при прямом, обратном и концевом порядке обхода.
4. Изобразите графически дерево, заданное с помощью вложенных скобок: (A(B(C, D), E), F, G).
5. Изобразите графически синтаксическое дерево для следующего арифметического выражения:
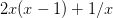
Запишите это выражение в обратной польской записи.
6. Для приведенного ниже графа (рис. 15) запишите матрицу смежности и матрицу инцидентности.

Рис. 15.
Задачи
1. Вычислив факториал достаточно большое количество раз (миллион или больше), сравните эффективность рекурсивного и итерационного алгоритмов. Во сколько раз будет отличаться время выполнения и как это отношение будет зависеть от числа, факториал которого рассчитывается?
2. Напишите рекурсивную функцию, проверяющую правильность расстановки скобок в строке. При правильной расстановке выполняются условия:
(а) количество открывающих и закрывающих скобок равно.
(б) внутри любой пары открывающая – соответствующая закрывающая скобка, скобки расставлены правильно.
Примеры неправильной расстановки:)(, ())(, ())(() и т.п.
3. В строке могут присутствовать скобки как круглые, так и квадратные скобки. Каждой открывающей скобке соответствует закрывающая того же типа (круглой – круглая, квадратной- квадратная). Напишите рекурсивную функцию, проверяющую правильность расстановки скобок в этом случае.
Пример неправильной расстановки: ([) ].
4. Число правильных скобочных структур длины 6 равно 5: ()()(), (())(), ()(()), ((())), (()()).
Напишите рекурсивную программу генерации всех правильных скобочных структур длины 2 n.
Указание: Правильная скобочная структура минимальной длины «()». Структуры большей длины получаются из структур меньшей длины, двумя способами:
(а) если меньшую структуру взять в скобки,
(б) если две меньших структуры записать последовательно.
5. Создайте процедуру, печатающую все возможные перестановки для целых чисел от 1 до N.
6. Создайте процедуру, печатающую все подмножества множества {1, 2, …, N}.
7. Создайте процедуру, печатающую все возможные представления натурального числа N в виде суммы других натуральных чисел.
8. Создайте функцию, подсчитывающую сумму элементов массива по следующему алгоритму: массив делится пополам, подсчитываются и складываются суммы элементов в каждой половине. Сумма элементов в половине массива подсчитывается по тому же алгоритму, то есть снова путем деления пополам. Деления происходят, пока в получившихся кусках массива не окажется по одному элементу и вычисление суммы, соответственно, не станет тривиальным.
Замечание: Данный алгоритм является альтернативой приему накопления суммы. В случае вещественнозначных массивов он, обычно, позволяет получать меньшие погрешности округления.
9. Запрограммируйте быстрые методы сортировки массивов, описанные в разделе 6.4.
10. Создайте процедуру, рисующую кривую Коха (рис. 12).
11. Воспроизведите рис. 16. На рисунке на каждой следующей итерации окружности в 2.5 раза меньше (этот коэффициент можно сделать параметром).
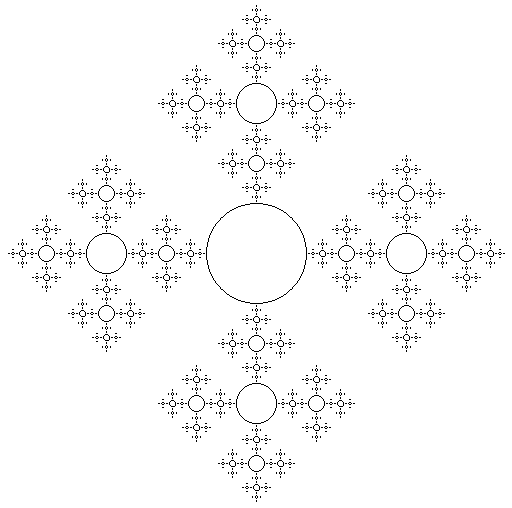
Рис. 16.
Date: 2016-07-18; view: 593; Нарушение авторских прав