
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Примеры рекурсивных алгоритмов
|
|
Рисование дерева
Рассмотрим алгоритм рисования деревца, изображенного на рис. 6. Если каждую линию считать узлом, то данное изображение вполне удовлетворяет определению дерева, данному в предыдущем разделе.
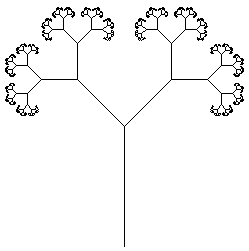
Рис. 6. Деревце.
Рекурсивная процедура, очевидно должна рисовать одну линию (ствол до первого разветвления), а затем вызывать сама себя для рисования двух поддеревьев. Поддеревья отличаются от содержащего их дерева координатами начальной точки, углом поворота, длиной ствола и количеством содержащихся в них разветвлений (на одно меньше). Все эти отличия следует сделать параметрами рекурсивной процедуры.
Пример такой процедуры, написанный на Delphi, представлен ниже:
| procedure Tree( Canvas: TCanvas; //Canvas, на котором будет рисоваться дерево x,y: extended; //Координаты корня Angle: extended; //Угол, под которым растет дерево TrunkLength: extended; //Длина ствола n: integer //Количество разветвлений (сколько еще предстоит //рекурсивных вызовов) ); var x2, y2: extended; //Конец ствола (точка разветвления) begin x2:= x + TrunkLength * cos(Angle); y2:= y - TrunkLength * sin(Angle); Canvas.MoveTo(round(x), round(y)); Canvas.LineTo(round(x2), round(y2)); if n > 1 then begin Tree(Canvas, x2, y2, Angle+Pi/4, 0.55*TrunkLength, n-1); Tree(Canvas, x2, y2, Angle-Pi/4, 0.55*TrunkLength, n-1); end; end; |
Для получения рис. 6 эта процедура была вызвана со следующими параметрами:
| Tree(Image1.Canvas, 175, 325, Pi/2, 120, 15); |
Заметим, что рисование осуществляется до рекурсивных вызовов, то есть дерево рисуется в прямом порядке.
Ханойские башни
Согласно легенде в Великом храме города Бенарас, под собором, отмечающим середину мира, находится бронзовый диск, на котором укреплены 3 алмазных стержня, высотой в один локоть и толщиной с пчелу. Давным-давно, в самом начале времен монахи этого монастыря провинились перед богом Брамой. Разгневанный, Брама воздвиг три высоких стержня и на один из них поместил 64 диска из чистого золота, причем так, что каждый меньший диск лежит на большем. Как только все 64 диска будут переложены со стержня, на который Бог Брама сложил их при создании мира, на другой стержень, башня вместе с храмом обратятся в пыль и под громовые раскаты погибнет мир.
В процессе требуется, чтобы больший диск ни разу не оказывался над меньшим. Монахи в затруднении, в какой же последовательности стоит делать перекладывания? Требуется снабдить их софтом для расчета этой последовательности.
Независимо от Брамы данную головоломку в конце 19 века предложил французский математик Эдуард Люка. В продаваемом варианте обычно использовалось 7-8 дисков (рис. 7).

Рис. 7. Головоломка «Ханойские башни».
Предположим, что существует решение для n -1 диска. Тогда для перекладывания n дисков надо действовать следующим образом:
1) Перекладываем n -1 диск.
2) Перекладываем n -й диск на оставшийся свободным штырь.
3) Перекладываем стопку из n -1 диска, полученную в пункте (1) поверх n -го диска.
Поскольку для случая n = 1 алгоритм перекладывания очевиден, то по индукции с помощью выполнения действий (1) – (3) можем переложить произвольное количество дисков.
Создадим рекурсивную процедуру, печатающую всю последовательность перекладываний для заданного количества дисков. Такая процедура при каждом своем вызове должна печатать информацию об одном перекладывании (из пункта 2 алгоритма). Для перекладываний из пунктов (1) и (3) процедура вызовет сама себя с уменьшенным на единицу количеством дисков.
| //n – количество дисков //a, b, c – номера штырьков. Перекладывание производится со штырька a, //на штырек b при вспомогательном штырьке c. procedure Hanoi(n, a, b, c: integer); begin if n > 1 then begin Hanoi(n-1, a, c, b); writeln(a, ' -> ', b); Hanoi(n-1, c, b, a); end else writeln(a, ' -> ', b); end; |
Заметим, что множество рекурсивно вызванных процедур в данном случае образует дерево, проходимое в обратном порядке.
Date: 2016-07-18; view: 475; Нарушение авторских прав