Расчет информационных характеристик канала

Исходный сигнал был продискретизирован в соответствии с теоремой Котельникова, т.е. преобразован в последовательность равноотстоящих по времени отсчетов. Полученная выборка отсчетов позволяет передать информацию об исходном сигнале без потерь.

Таким образом, сформированную выборку можно рассматривать как алфавит источника информации с равновероятными символами. Известно, что для описания источника используется определенный набор информационных характеристик: количество информации на символ, энтропия, производительность и избыточность источника.

Для дальнейших расчетов вычислим производительность источника, определяющую скорость формирования информационных символов:

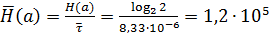бит/c, (5.1)

где 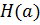– энтропия источника алфавита; – среднее время генерации одного знака алфавита.

Рассматривая принципы и предельные возможности непосредственного согласования дискретного источника сообщений с непрерывным каналом связи, следует напомнить, что в непрерывном канале надо знать плотности распределения случайных процессов сигналов, помех и их условные плотности распределения. Это понятие вводится при моделировании канала связи, и с точки зрения передачи сообщений нет большого противоречия в том, что источник принят дискретным, а канал непрерывен.

Полоса пропускания канала должна быть достаточной для прохождения спектра модулированного сигнала. Величина 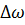была определена в п. 4.3.

Предельные возможности согласования дискретного источника с непрерывным каналом определяются теоремой Шеннона, которая аналогично звучит в случае дискретного источника и дискретного канала.

Теорема Шеннона: если дискретные сообщения, выдаваемые дискретным источником с производительностью 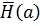можно закодировать так, что при передаче по гауссову каналу с белым шумом, пропускная способность C которого превышает 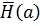, то вероятность ошибки 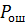может быть достигнута сколь угодно малой.

При определении пропускной способности канала статистические законы распределения помехи, сигнала, и суммы сигнала и помехи – нормальные законы с соответствующими дисперсиями 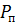, 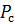и .

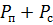Пропускная способность гауссова канала равна:

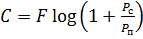, (5.2)

где 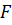– частота дискретизации; 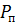– мощность помехи.

Мощность помехи определяется по заданной спектральной плотности мощности 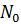и полосе частот модулированного сигнала :

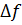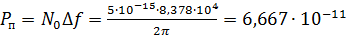Вт. (5.3)

Определим производительность источника:

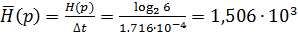бит/с.

Пользуясь теоремой Шеннона, определим мощность, обеспечивающую передачу по каналу:

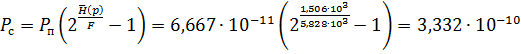Вт.

Date: 2016-07-18; view: 351; Нарушение авторских прав