
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

III Общие выводы по результатам проведенного эконометрического анализа
|
|
3.1 Оценка уравнения тренда. Уравнение тренда имеет вид:
 =1.21t +110.69
=1.21t +110.69
Но в связи с тем, что относительная ошибка 20,9%, что больше 10%. Уравнением пользоваться нельзя.
3.3 Основная тенденция изменения показателя во времени. Ожидаемое значение показателя «Среднегодовая численность работников, y» для 14-го периода при первом методе: будет равно 94.91, при втором методе: равно 102.81
3.4 Прогнозный интервал показателя 57,624  t
t  180,836
180,836
.
IV Эконометрический анализ данных на основе регрессионной модели:
4.1 Анализ исходных данных
Построим графики зависимостей x(t), y(t), y(x) (рис. 2-4)



Вывод: Графический анализ исходных данных показывает, что для построения модели регрессии может быть использовано уравнение прямой
Y(x)=. a0 +a1x
4.2. Построение модели регрессии y(x).
В соответствии с методом наименьших квадратов (МНК) для определения
параметров а0 и а1 решим систему уравнений:
 |
na0+a1∑x=∑y
a0∑x+a1∑x2=∑xy
Для удобства вычислений параметров системы уравнений составим таблицу
Таблица 4
| n | x | y | x^2 | xy |
| сумма |
 Исходя из табл.4, система уравнений с численными значениями параметров имеет вид:
Исходя из табл.4, система уравнений с численными значениями параметров имеет вид:
13а0+70450а1=1439
70450а0+433930314а1=7980818
Решим систему уравнений по правилу Крамера:
D0=  = 677891582
= 677891582
D1= 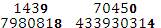 = 62177093746
= 62177093746
D3=  = 2373084
= 2373084
a0=  =
=  = 91,72
= 91,72
a1= 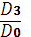 =
=  = 0,0035
= 0,0035
Вывод: Модель регрессии с численными оценками коэффициентов имеет вид:
 (x)= 0,0035x+91,72
(x)= 0,0035x+91,72
4.3 Анализ качества модели регрессии – анализ остатков
Определим остатки по формуле (см. табл. 5):
ui=yi -  i
i
Таблица 5
| n | Xi | Yi |  i i
| ui=yi -  i i
| ui- ui-1 | (ui- ui-1)2 | ui2 |
| 107,8305 | -11,8305 | 139,9607 | |||||
| 105,9055 | -47,9055 | -36,075 | 1301,406 | 2294,937 | |||
| 125,5475 | 9,4525 | 57,358 | 3289,94 | 89,34976 | |||
| 109,731 | 43,269 | 33,8165 | 1143,556 | 1872,206 | |||
| 108,695 | -0,695 | -43,964 | 1932,833 | 0,483025 | |||
| 116,682 | -11,682 | -10,987 | 120,7142 | 136,4691 | |||
| 113,6195 | -37,6195 | -25,9375 | 672,7539 | 1415,227 | |||
| 117,7425 | 1,2575 | 38,877 | 1511,421 | 1,581306 | |||
| 118,18 | -0,18 | -1,4375 | 2,066406 | 0,0324 | |||
| 106,105 | 42,895 | 43,075 | 1855,456 | 1839,981 | |||
| 102,213 | -3,213 | -46,108 | 2125,948 | 10,32337 | |||
| 107,2705 | 20,7295 | 23,9425 | 573,2433 | 429,7122 | |||
| 99,413 | -4,413 | -25,1425 | 632,1453 | 19,47457 | |||
| сумма | 1438,935 | 0,065 | 7,4175 | 15161,48 | 8249,738 |
Вычислим коэффициент Дарбина-Уотсона dr (промежуточные вычисления выполнены в табл. 5)

Коэффициент dr является критерием проверки гипотезы о наличии автокорреляции в остатках генеральной совокупности. По таблице Дарбина Уотсона находим для заданного уровня значимости  и числа наблюдений n= 13 теоретические значения
и числа наблюдений n= 13 теоретические значения  =0.86 и
=0.86 и  = 1.56.
= 1.56.
Для сравнения табличных и расчетных значений построим схему:
| Присутствует автокорр «+» | Зона неопределенности | Автокорр отсутствует | Зона неопределенности | Присутствует автокорр «- |
0 d d 4-d 4-d 4
0.86 1.56 1.83 2.44 3.14
Вывод: Критерий Дербина- Уотсона dr=1.83 подтверждает гипотезу о отсутствии автокорреляции в остатках.
4.4. Корреляционный анализ данных.
Рассчитаем линейный коэффициент корреляции по формуле:

| n | x | y | x*y | x^2 | y^2 |
| сумма | |||||
| средн | 5419,2308 | 110,6923 | 7798273,08 | 381784807,7 | 159286,2308 |
rxy= (7798273.08-5419.23*110.69)/((381784807.7-(5419.23)2) *(159286.2308-(110.69)2))0.5 = 0,268
rxy = 0.268 меньше 0,3
Вывод: Величина коэффициента корреляции = 0.268 свидетельствует о связь прямая и слабая между показателями х и у
Выполним проверку статистической значимости линейного коэффициента корреляции с помощью критерия Стьюдента (t- статистики):
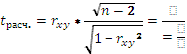
= 0,268 * ((13-2)0,5)/(1-0,2682) 0,5 =0,923
Табличное значение критерия Стьюдента определим, используя группу функций «Статистические», функция СТЬЮДРАСПОБР (для MSExcel - 2007; в зависимости от года MSExcel название функции может немного меняться).
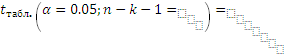 = 12,7062
= 12,7062
где 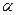 = 0,05 – уровень значимости; n – число заданных значений y;
= 0,05 – уровень значимости; n – число заданных значений y;
k – количество независимых переменных (х) в уравнении регрессии.
Сравним 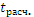 меньше
меньше  :
:
Вывод: Проверка статистической значимости линейного коэффициента корреляции r показывает, что коэффициент не значимо отличен от нуля.
Общий вывод: Корреляционный анализ показал, что между показателями x и y имеется слабая прямая взаимосвязь.
Date: 2016-07-18; view: 645; Нарушение авторских прав