
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

II. Прогноз показателя на следующий период времени несколькими способами.
|
|
Прогнозирование показателей на основе рядов динамики может осуществляться тремя основными методами.
Первый метод заключается в использовании для прогнозирования среднего абсолютного изменения значений элементов ряда, которое определяется по выражению:
| n | y | yi-yi-1 |
| -38 | ||
| -45 | ||
| -3 | ||
| -29 | ||
| -1 | ||
| -50 | ||
| -33 | ||
| ∑ | -1 |
 =
=  -1/13-1= -0.083
-1/13-1= -0.083
Где: yi, yi-1 - текущее и предшествующее фактические значения показателя; n- число элементов исходного ряда;
Общее выражение для прогнозирования по первому методу анализа рядов динамики имеет вид:
Y,m = yn +m*∆Ȳ =95+1*-0.083= 94.91
Где: yn – фактическое значение последнего элемента ряда;
m – число шагов прогноза (на один период вперед – m=1, на два периода - m=2 и т.д.).
Вывод: Ожидаемое значение показателя «Среднегодовая численность работников, y» для 14-го периода будет равно 94.91
Второй метод обеспечивает выполнение прогноза с использованием среднего коэффициента роста исходного ряда по выражению:
Y,m = yn *km cp = 95 *1.082 = 102,81
km cp - текущее значение коэффициент роста ряда динамики;
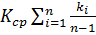 =12.9866/13-1=1.082
=12.9866/13-1=1.082
, 
Где  – текущее значение коэффициент роста ряда динамики
– текущее значение коэффициент роста ряда динамики
| n | y | Ki |
| 0,604166667 | ||
| 2,327586207 | ||
| 1,133333333 | ||
| 0,705882353 | ||
| 0,972222222 | ||
| 0,723809524 | ||
| 1,565789474 | ||
| 0,991596639 | ||
| 1,262711864 | ||
| 0,66442953 | ||
| 1,292929293 | ||
| 0,7421875 | ||
| ∑ | 12,98664461 |
Вывод: Ожидаемое значение показателя Y для t = 14 равно 102.81
Третий метод обеспечивает прогнозирование значений показателя на основе уравнения тренда и состоит из следующих основных этапов:
1) Построение уравнения тренда
2) Расчет теоретических значений показателя по уравнению тренда;
3) Расчет ошибки прогнозирования;
4) Определение границ прогнозного интервала.
1) Это задание выполняется на ПЭВМ, с использованием функций табличного процессора MS Excel:
- Для вывода уравнения тренда используется группа функций «Статистические», функция «Тенденция».
| Тенденция | 119,2308 |
| Критер. Стьюдента | 2,200985 |
- Для определения табличного (критического) значения критерия Стьюдента используется группа функций «Статистические», функция СТЬЮДРАСПОБР (для MS Excel-2007; в зависимости от года MS Excel название функций может меняться).
2) Расчет теоретических значений показателя по уравнению тренда и определение остатков:
Таблица 3
| n | t | y(t) | |y(t)-y| | |y(t)-y|^2 |
| -6 | 103,43 | 7,43 | 55,2049 | |
| -5 | 104,64 | 46,64 | 2175,2896 | |
| -4 | 105,85 | 29,15 | 849,7225 | |
| -3 | 107,06 | 45,94 | 2110,4836 | |
| -2 | 108,27 | 0,27 | 0,0729 | |
| -1 | 109,48 | 4,48 | 20,0704 | |
| 110,69 | 34,69 | 1203,3961 | ||
| 111,9 | 7,1 | 50,41 | ||
| 113,11 | 4,89 | 23,9121 | ||
| 114,32 | 34,68 | 1202,7024 | ||
| 115,53 | 16,53 | 273,2409 | ||
| 116,74 | 11,26 | 126,7876 | ||
| 117,95 | 22,95 | 526,7025 | ||
| ∑ | 1438,97 | 266,01 | 8617,9955 |
3) Ошибка прогнозирования – εt определяется по формуле: εt=tαϬε, где tα= f (n-m;Δ P)- табличное значение критерия Стьюдента;
n-m - число степеней свободы;
n- число элементов ряда динамики;
m- число параметров уравнения тренда;
Δ P= 0,05 (5 %) –принятый уровень значимости вероятности.
Ϭε- стандартное отклонение ошибки,

Ϭε=  =27,99025074
=27,99025074
εt=tαϬε =2,200985*27,99025074≈ 61,606
4) Определение границ прогнозного интервала, на котором будет находится прогнозное значение величины  t c вероятностью P=0,95:
t c вероятностью P=0,95:
 t- εt
t- εt  t
t  t+ εt
t+ εt
T 180,836
Вывод: Прогнозное значение показателя  t =119,23 для t=14 находиться в пределах от 57,624 до 180,836 с вероятностью P= 0,95.
t =119,23 для t=14 находиться в пределах от 57,624 до 180,836 с вероятностью P= 0,95.
Date: 2016-07-18; view: 1225; Нарушение авторских прав