Операции над множествами

Обозначение множеств и их элементов. Равенство множеств.

Подмножество (включение). Сумма (объединение) множеств.

Произведение (пересечение) множеств. Разность (дополнение)

множеств.Симметричная разность множеств. Свойства

операций над множествами.

Множества обозначаются заглавными латинскими буквами, а их элементы – строчными. Запись a R означает, что элемент а принадлежит множеству R, то есть а является элементом множества R. В противном случае, когда а не принадлежит множеству R, пишут a R.

Два множества А и В называются равными (А = В), если они состоят изодних и тех же элементов, то есть каждый элемент множества А является элементом множества В и наоборот, каждый элемент множества В является элементом множества А.

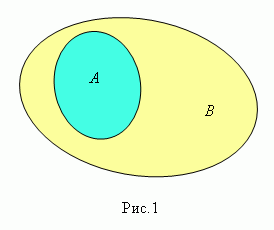
Говорят, что множество А содержится в множестве В (рис.1) или множество А является подмножеством множества В (в этом случае пишут А В), если каждый элемент множества А одновременно является элементом множества В. Эта зависимость между множествами называется включением. Для любого множества А имеют место включения: А и А А.

Сумма (объединение) множеств А и В (пишется А В) есть множество элементов, каждый из которых принадлежит либо А, либо В. Таким образом, е А В тогда и только тогда, когда либо е А,либо е В.

Произведение (пересечение) множеств А и В (пишется А В, рис.2) есть множествоэлементов, каждый из которых принадлежит и А, и В. Таким образом, е А В тогда и только тогда, когда е А и е В.

Разность множеств А и В (пишется А – В, рис.3) есть множествоэлементов, которые принадлежат множеству А, но не принадлежат множеству В. Это множество называется также дополнением множества В относительно множества А.

Симметричная разность множеств А и В (пишется А \ В) есть множество:

А \ В = (А – В) (В – А).

Свойства операций над множествами: