Дисконтирование представляет собой процесс нахождения величины на заданный момент времени по ее известному или предполагаемому значению в будущем (от будущего к настоящему).

В экономическом смысле величина P, найденная в процессе дисконтирования, показывает современное (с позиции текущего момента времени) значение будущей величины S.

Нетрудно заметить, что дисконтирование, по сути, является зеркальным отражением наращения. Используемую при этом процентную ставку i называют нормой дисконта, учетной или дисконтной ставкой.

В финансовой литературе проценты, полученные по ставке наращения, принято называть декурсивными, по учетной ставке – антисипативными.

Декурсивный способ начисления процентов. Проценты начисляются в конце каждого интервала начисления. Их величина определяется исходя из величины предоставляемого капитала. Соответственно, декурсивная процентная ставка, или, что то же, ссудный процент, представляет собой выраженное в процентах отношение суммы начисленного за определенный интервал дохода к сумме, имеющейся на начало данного интервала.

Антисипативный способ (предварительный) начисления процентов. Проценты начисляются в начале каждого интервала начисления. Сумма процентных денег определяется исходя из наращенной суммы. Процентной ставкой будет выраженное в процентах отношение суммы дохода, выплачиваемого за определенный интервал, к величине наращенной суммы, полученной по прошествии этого интервала.

В зависимости от условий проведения финансовых операций, как наращение, так и дисконтирование, могут осуществляться с применением простых, сложных либо непрерывных процентов.

Как правило, простые проценты используются в краткосрочных финансовых операциях, срок проведения которых меньше года. Базой для исчисления процентов за каждый период в этом случае является первоначальная (исходная) сумма сделки.

В общем случае, наращение и дисконтирование по ставке простых процентов осуществляют по следующим формулам:

S = P (1+ n* i),

P = S / (1 + n * i)

n = t / K

где n – продолжительность периода начисления в годах;

t – число дней ссуды;

K – число дней в году;

i – ставка процентов.

Сложные проценты широко применяются в долгосрочных финансовых операциях, со сроком проведения более одного года. Вместе с тем они могут использоваться и в краткосрочных финансовых операциях, если это предусмотрено условиями сделки, либо вызвано объективной необходимостью (например, высоким уровнем инфляции, риска и т.д.). При этом база для исчисления процентов за период включает в себя как исходную сумму сделки, так и сумму уже накопленных к этому времени процентов.

S = P (1 + i_c)ⁿ,

где i_c – относительная величина годовой ставки сложных процентов.

На рис. 1.1 приведен график, отражающий рост суммы в 1,00 при различных ставках сложных процентов.

Рис. 1.1. Рост суммы в 1.00 по ставкам сложных процентов

Начисление сложных процентов может осуществляться не один, а несколько раз в году – по полугодиям, кварталами и т.д. В том случае оговаривается номинальная ставка процентов j – годовая ставка, по которой определяется величина ставки процентов, применяемая на каждом интервале начисления.

Итак, пусть годовая ставка равна j, число периодов начисления в году – m. Каждый раз проценты начисляются по ставке j/m. Тогда формулу наращения теперь можно представить следующим образом:

S = P(1 + j/m)^N,

где N – общее количество периодов начисления.

Если N целое число (N=mn), то в большинстве случаев для определения величины множителя наращения можно воспользоваться таблицей сложных процентов.

Нетрудно догадаться, что чем чаще начисляются проценты, тем быстрее идет процесс наращения (цепной процесс).

Тогда формулы для дисконтирования по сложной ставке процентов имеют вид:

P = S / (1 + i_c)ⁿ или

P = S / (1 + j/m)^mn.

На рис 1.2 приведена графическая диаграмма, отражающая процесс дисконтирования суммы в 1,00 при различных ставках сложных процентов.

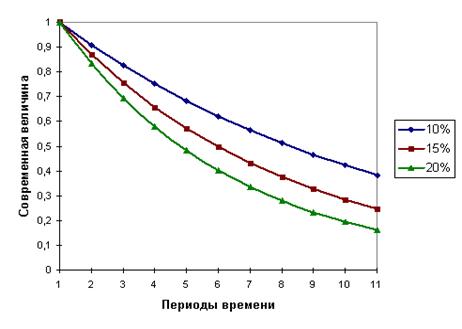
Рис. 1.2. Дисконтирование суммы в 1,00 при различных ставках i_c

Как и следовало ожидать, величина P также зависит от продолжительности операции и процентной ставки, однако зависимость здесь обратная – чем больше i_c и n, тем меньше текущая (современная) величина.

Непрерывные проценты представляют главным образом теоретический интерес и редко используются на практике. Они применяются в особых случаях, когда вычисления необходимо производить за бесконечно малые промежутки времени. Существенно большее значение непрерывное наращение имеет в анализе сложных финансовых проблем, например при обосновании и выборе инвестиционных решений, в финансовом проектировании. С помощью непрерывных процентов удается учесть сложные закономерности процесса наращения, например, использовать изменяющиеся по определенному закону процентные ставки.

Методы наращения и дисконтирования играют важную роль в финансовом анализе, так как являются инструментарием для оценки потоков платежей (cash flows).

 

На всякий случай, вдруг пригодится.

Для того чтобы сопоставить результаты наращения по разным процентным ставкам, достаточно сравнить соответствующие множители наращения. Нетрудно убедиться в том, что при одинаковых уровнях процентных ставок соотношения этих множителей существенно зависят от срока. В самом деле, при условии, что временная база для начисления процентов одна и та же, находим следующие соотношения:

- для срока меньше года простые проценты больше сложных:

(1 + ni) > (1 + i_c)ⁿ

- для срока больше года сложные проценты больше простых:

(1 + i_c)ⁿ > (1 + ni)

- для срока, равного году, множители наращения равны друг другу.

Заметим также, что при n > 1 с увеличением срока различие в последствиях применения простых и сложных процентов усиливается. Графическую иллюстрацию соотношения множителей наращения см. на рис. 1.3. В табл. 1 приведены значения множителей наращения для i = i_с = 12%, K = 365.

 

S

(1+ i)ⁿ

 

1+ ni

 

Р

 

0 1 n

Табл. 1.

Множители наращения	Срок ссуды
30 дней	180 дней	1 год	5 лет	10 лет	100 лет
1+ni	1.01644	1.05918	1.12	1.6	2.2
(1+i)n	1.00936	1.05748	1.12	1.76234	3.10584	83522.3

 

Date: 2016-11-17; view: 566; Нарушение авторских прав