Метод импликантных матриц

Для поиска минимальной формы функции пользуются методом импликантных матриц. Существо метода заключается в следующем: составляется импликантная матрица, колонки которой именуются конституентами единицы, а строки – простыми импликантами. Затем находится минимальное покрытие всех конституент единицы простейшими импликантами. При этом ищется такая минимальная совокупность простых импликант, которые совместно покрывают все конституенты единицы исходной функции. Факт покрытия отмечается в клетке матрицы символом * (звездочка) в случае, когда импликанта покрывает соответствующую конституенту (является ее собственной частью). Из всех простых импликант выбираются вначале только такие, которые только одни покрывают конституенты единицы (в колонке матрицы только один символ покрытия), затем производится перебор.

Пример:

Из матрицы видно, что в минимальную форму функции обязательно войдут импликанты n (покрывает конституенту F), импликанта r (покрывает конституенту D). То же справедливо отностительно импликанты p. Что касается остальных, то нужно выбрать минимальную совокупность.

Итак:

f¹_min = n r p q

f²_min = n r p m

Т.е. данная функция имеет две одинаково минимальные формы.

Замечание: важным обстоятельством, усложняющим минимизацию функций, является присутствие перебора различных вариантов при поиске оптимального покрытия.

Минимизирующие диаграммы Этот метод графической минимизации был изложен Карно, который ввел в употребление специальные карты. Эти карты позволяют для функции, зависящей от небольшого числа аргументов (до пяти - шести) находить результаты всех возможных склеек. Карты впоследствии были усовершенствованы Вейчем, а сам метод иногда именуется как метод минимизации с помощью диаграмм Вейча. Рассмотрим существо способа для функций, зависящих от 2, 3 и 4-х переменных. Функции 2-х переменных Диаграмма – матрица, столбцам и строкам которой приписывается смысл переменных, входящих в функцию в прямом или инверсном виде. В клетках матрицы ставится произведение, образованное из букв, которыми названы строки и столбцы матрицы. Обратим внимание на то, что данная матрица сразу указывает на возможную склейку произведений, входящих в выражение функции. Так склейке подлежат все произведения, расположенные в соседних по вертикали и горизонтали клетках. xy склеивается с xy и с xy; xy склеивается с xy и с xy; xy склеивается с xy и с xy; xyсклеивается с xy и с xy; Более того, эта же диаграмма дает и результат склейки: это название или строки, или столбца. При минимизации по данному методу заполняется диаграмма функции 2-х переменных по следующему правилу: если то или иное произведение входит в СДНФ функции, то в соответствующую ему клетку диаграммы ставится единица, и нуль – в противном случае. Если в диаграмме находится хотя бы две соседние единицы, то это означает, что два произведения склеиваются, а результатом склейки является произведение (в данном случае из одной буквы), именем которого названа данная строка или столбец. Пример: f(x,y) = xy xy xy Выделим в диаграмме соседние единицы, и результат склейки дает минимальную форму функции: fmin(x,y) = x y Заметим, что результатом склейки является результат покрытия конституент единицы исходной функции простыми импликантами. В данном случае переменными, которыми названы строки и столбцы диаграммы. Функции 3-х переменных Для минимизации функций, зависящих от трех переменных, применяется следующая диаграмма: Из диаграммы видно, что склейке подлежат все произведения, расположенные в соседних клетках, а также в клетках, расположенных на краях диаграммы. Результат склейки – есть произведения, содержащее на одну букву меньше. Видно также, что возможна и дальнейшая склейка, однако уже между произведениями, расположенными во взаимно перпендикулярном направлении. 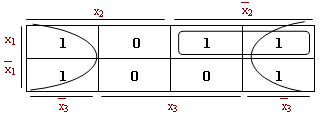Рассмотрим, например, левую половину диаграммы: x1x2x3 x1x2x3 x1x2x3 x1x2x3 Склеим попарно произведения, стоящие в строках: x1x2 x1x2 x1x2 x1x2 Теперь видим, что можно произвести дальшейшую склейку, но произведений, стоящих в столбцах матрицы: x2 x2 x2 x2 Как видно, результат склейки – произведение x2. Именно эта переменная покрывает все четыре конституенты единицы СДНФ функции. Подобное же утверждение справедливо и для конституент, расположенных в строках и столбцах диаграммы по краям таблицы. Таким образом, при поиске минимальной формы необходимо считать левый край таблицы склеенным с правым. Говорят, что для наглядности можно условно данную диаграмму представить нанесенной на поверхность цилиндра. Пример: f(x1x2x3) = x1x2x3 x1x2x3 x1x2x3 x1x2x3 x1x2x3 fmin(x1x2x3) = x3 x1x2 Видим, что две единицы, соответствующие конституентам x1x2x3 и x1x2x3, покрываются произведением x1x2.

Date: 2016-05-14; view: 1173; Нарушение авторских прав