Главная Случайная страница


Полезное:

Как сделать разговор полезным и приятным Как сделать объемную звезду своими руками Как сделать то, что делать не хочется? Как сделать погремушку Как сделать так чтобы женщины сами знакомились с вами Как сделать идею коммерческой Как сделать хорошую растяжку ног? Как сделать наш разум здоровым? Как сделать, чтобы люди обманывали меньше Вопрос 4. Как сделать так, чтобы вас уважали и ценили? Как сделать лучше себе и другим людям Как сделать свидание интересным?


Категории:

АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника






Свойства диаграмм Вейча

⇐ ПредыдущаяСтр 15 из 32Следующая ⇒

С помощью диаграмм Вейча можно находить:

  1. минимальную форму по СКНФ
  2. минимальную форму по ДНФ и КНФ функции
  3. все одинаково минимальные формы
  4. минимальную форму неполностью определенных функций.

Пусть f(x1x2x3) задана не в виде СДНФ, а в ДНФ:

f(x1x2x3) = x1x2 x1x2x3 x1x2

Заполним соответствующую диаграмму:

Так как x1x2 = x1x2 (x3 x3) = x1x2x3 x1x2x3, то в соответствующие клетки диаграммы поставлены единицы.

Поэтому: fmin(x1,x2,x3) = x2x3 x1x2 x1x2

Преимущество метода: простота и наглядность для небольшого числа аргументов.

Недостатки: неприменяемость метода для большого числа аргументов (> 6) вследствие сложности диаграмм и потери наглядности.

5. Лекция: Минимизация неполностью определенных функций
Страницы: 1 | 2 | 3 | вопросы |» | учебники | для печати и PDA | ZIP
Если Вы заметили ошибку - сообщите нам, или выделите ее и нажмите Ctrl+Enter
В лекции представлена минимизация неполностью определенных функций, дан синтез функций в базисах штрих Шеффера и стрелка Пирса, даны подходы к минимизации конъюнктивных форм.
Очень часто, если не в большинстве случаев, работа конкретного устройства описывается с помощью неполностью определенной функции, так как некоторые комбинации входных сигналов не подаются или являются запрещенными. Определение. Неполностью определенной функцией является такая переключательная функция, значения которой на некоторых наборах аргументов могут быть произвольными (т.е. равными "0" или "1"). Определение. Пусть функция f(x1,x2,...xn) не определена на "р" наборах аргументов. Тогда полностью определенную функцию (x1,x2,...xn) будем считать эквивалентной к f(x1,x2,...xn), если ее значения на тех наборах, на которых f(x1,x2,...xn) определена, совпадают. Очевидно, существует 2р различных функций, эквивалентных f(x1,x2,...xn). Задача минимизации f(x1,x2,...xn) состоит в выборе такой эквивалентной (x1,x2,...xn), которая имеет простейшую форму. Введем две вспомогательные эквивалентные функции 0(x1,x2,...xn), 1(x1,x2,...xn), которые принимают на запрещенных наборах аргументов значения 0 и 1 соответственно. ТЕОРЕМА. МДНФ неполностью определенной f(x1,x2,...xn) совпадает с дизъюнкцией самых коротких импликант 1(x1,x2,...xn), которые совместно накрывают все конституенты единицы 0(x1,x2,...xn), и ни одна из которых не является лишней. Пример: Пусть задана f(x1,x2,...xn) в виде следующей таблицы:
f(x1,x2,...xn)   - - -             -     - -  
Числовые эквиваленты наборов                                

Тогда

0(x1x2x3x4) = 0 5 8 12 15 = x1x2x3x4 x1x2x3x4 x1x2x3x4 x1x2x3x4 x1x2x3x4 = 0000 0101 1000 1100 1111,

а

1(x1x2x3x4) = 0 1 2 3 5 8 10 12 13 14 15 = 0000 0001 0010 0011 0101 1000 1010 1100 1101 1110 1111

Найдем простые импликанты 1(x1x2x3x4)

Конституенты единицы 1 Отметки о склейке Импликанты Отметки о склейке Импликанты
  *   000- 00-0 -000 * 00- - 00- - -0-0
  * *
* *
*   00-1 0-01 001- -010 1-00 *
  * -
* * 1- -0
* *
* *
      *   -101 1-10 110- 11-0 -
*
  * - 11- -
-
  * 111- *

Простые импликанты 1(x1x2x3x4)

1(x1x2x3x4) = 0-01 -101 110- 11-0 00- - -0-0 1- -0 11- -

Построим импликантную матрицу.

Конституенты единицы 0          
Простые импликанты 1
0-01   +      
-101   +      
110-       +  
11-0       +  
00-- +        
-0-0 +   +    
1--0     + +  
11--       + +

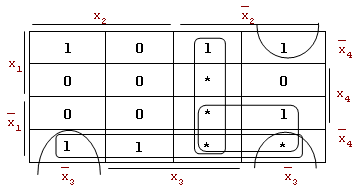
Выполним оптимальное покрытие конституент единицы 0 простыми импликантами 1 и получаем минимальную форму функции f(x1x2 x3 x4)

f1min(x1x2 x3 x4) = 11- - -0-0 -101 = x1x2 x2x4 x2x3x4

f2min(x1x2 x3 x4) = 11- - -0-0 0-01 = x1x2 x2x4 x1x3x4

Минимизация с помощью диаграмм Вейча неполностью определенных функций в наглядной и удобной форме позволяет отыскать минимальные формы.


Пример:

Рассмотрим функцию f(x1x2 x3 x4) и найдем ее минимальную форму. Заполнить диаграмму Вейча по следующим правилам: в клетки диаграммы поставим единицы, которые соответствуют конституентам единицы, нули – для отсутствующих конституент и символ неопределенности – "*" (звездочка) – в остальные.

Видно, что в клетки для конституент: x1x2x3x4, x1x2x3x4, x1x2x3x4 целесообразно "поставить" единицы вместо символов неопределенности, так как в этом случае образуется правильная конфигурация 2-го ранга, которая покрывается произведением x2x3.

Аналогично и в клетку x1x2x3x4 нужно "поставить" единицу.

Итак, fmin(x1x2 x3 x4) = x2x3 x1x4 x3x4 x1x2.

Замечание. Все, что было сказано относительно минимизации функции, представленной в СДНФ или ДНФ справедливо для функции, заданной в СКНФ или КНФ.

В этом случае необходимо отыскивать правильные конфигурации, образованные нулями.

 


⇐ Предыдущая10111213141516171819Следующая ⇒





Date: 2016-05-14; view: 811; Нарушение авторских прав


mydocx.ru - 2015-2024 year. (0.011 sec.) Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав - Пожаловаться на публикацию