
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Динамика. Законы Ньютона. Импульс тела
|
|
ФИЗИКА

| 
|
| 
|
Тамбов 2011
МИНИСТЕРСТВО образованиЯ И НАУКИ РФ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«ТАМБОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ИМЕНИ Г. Р. ДЕРЖАВИНА»
ФИЗИКА
Рекомендовано методическим советом ИМФИ ТГУ им. Г.Р. Державина в качестве учебника для студентов
по специальности «Лечебное дело»

УДК
ББК
Рецензенты:
кафедра физики Тамбовского государственного технического университета;
доктор физико-математических наук, профессор А.А. Шибков.
| Составители: Федоров В.А., Кириллов А.М., Васильева С.В. Физика учебник / Министерство образования и науки РФ, Тамб. гос. ун-т им. Г.Р. Державина. Тамбов: Издательский дом ТГУ им. Г.Р. Державина, 2011. 86 с. В учебнике приведены сведения из общего курса физики, необходимые студентам при дальнейшем изучении курса медицинской физики. УДК ББК | ||
| Ó ГОУВПО «Тамбовский государственный университет имени Г. Р. Державина», 2011 | ||
СОДЕРЖАНИЕ
МЕХАНИКА............................................................................. 5
§ 1. Кинематика. Механическое движение. Основные понятия 5
§ 2. Линейная скорость....................................................... 6
§ 3. Ускорение..................................................................... 7
§ 4. Динамика. Законы Ньютона. Импульс тела................ 9
§ 5. Силы в механике......................................................... 11
§ 6. Энергия и работа........................................................ 16
§ 7. Динамика вращательного движения.......................... 18
§ 8. Механические колебания........................................... 20
§ 9. Затухающие колебания. Вынужденные колебания... 22
§ 10. Элементы статики..................................................... 23
МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА.......... 25
§ 11. Основы молекулярно-кинетической теории........... 25
§ 12. Уравнение состояния идеального газа.................... 26
§ 13. Основное уравнение кинетической теории............. 28
§ 14. Энергия молекулы.................................................... 29
§ 15. Длина свободного пробега молекулы..................... 30
§ 16. Явления переноса..................................................... 31
§ 17. Внутренняя энергия системы................................... 32
§ 18. Работа в термодинамике.......................................... 33
§ 19. Первый закон термодинамики................................. 34
§ 20. Теплоемкость............................................................ 34
§ 21. Изопроцессы идеального газа.................................. 35
§ 22. Адиабатный процесс................................................ 36
§ 23. Круговые процессы. Цикл Карно............................. 37
§ 24. Второй закон термодинамики.................................. 38
§ 25. Реальные газы........................................................... 40
§ 26. Жидкости................................................................... 41
§ 27. Смачивание и капиллярные явления........................ 42
§ 28. Течение жидкостей................................................... 44
§ 29. Уравнение Д. Бернулли............................................ 45
§ 30. Течение вязких жидкостей в трубах........................ 47
ЭЛЕКТРОСТАТИКА.............................................................. 47
§ 31. Электрические заряды. Закон Кулона..................... 47
§ 32. Электрическое поле. Напряженность поля............. 48
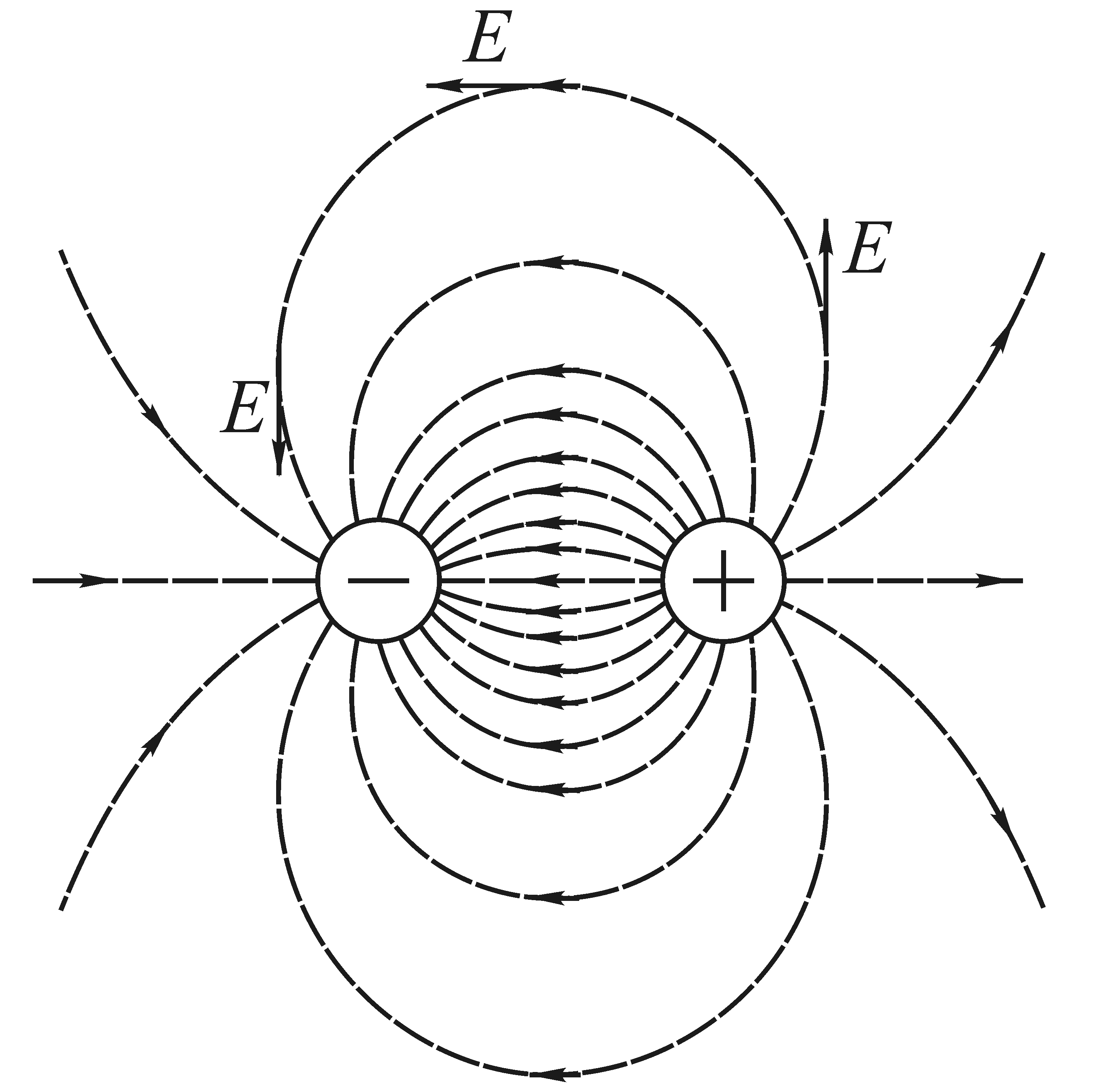
§ 33. Графическое изображение электростатических полей 50
§ 34. Работа, совершаемая при перемещении электрического заряда в электростатическом поле 50
§ 35. Проводники в электростатическом поле................. 52
§ 36. Электрическая емкость............................................ 52
§ 37. Диэлектрики в электрическом поле......................... 53
§ 38. Пьезоэлектрический эффект..................................... 54
§ 39. Энергия электрического поля.................................. 55
§ 40. Постоянный электрический ток. Сила и плотность тока 55
§ 41. Законы постоянного тока......................................... 56
§ 42. Электрический ток в жидкостях.............................. 57
§ 43. Электрический ток в газах....................................... 59
§ 44. Электрический ток в полупроводниках................... 60
ЭЛЕКТРОМАГНЕТИЗМ......................................................... 61
§ 45. Магнитное поле........................................................ 61
§ 46. Закон Ампера............................................................ 63
§ 47. Сила Лоренца............................................................ 63
§ 48. Магнитный поток...................................................... 64
§ 49. Электромагнитная индукция.................................... 64
§ 50. Вихревые токи (Токи Фуко)..................................... 65
§ 51. Явление самоиндукции............................................. 66
§ 52. Магнитные свойства вещества................................. 66
ГЕОМЕТРИЧЕСКАЯ ОПТИКА............................................. 68
§ 53. Законы геометрической оптики............................... 68
§ 54. Тонкая линза............................................................. 69
§ 55. Формула тонкой линзы............................................ 71
§ 56. Оптические приборы................................................ 72
ФИЗИЧЕСКАЯ ОПТИКА....................................................... 73
§ 57. Интерференция света............................................... 73
§ 58. Дифракция света....................................................... 74
§ 59. Поляризация света.................................................... 75
§ 60. Вращение плоскости поляризации.......................... 77
§ 61. Дисперсия, поглощение и рассеяние света............. 77
§ 62. Тепловое излучение.................................................. 78
§ 63. Строение атома......................................................... 79
§ 64. Рентгеновские лучи.................................................. 81
§ 65. Естественная радиоактивность................................ 82
Механика
Физику обычно начинают изучать с раздела «Механика». В Механике три части: кинематика, динамика, статика.
Кинематика. Механическое движение. Основные понятия
В разделе «Кинематика» изучают движение тел. Причины, которые вызывают движение тел, не учитывают. Основная задача кинематики найти путь, пройденный телом.
Механическое движение. Это изменение расположения тел или их частей относительно друг друга. Происходит движение в пространстве. Время тоже изменяется, отражая последовательность событий.
Группа тел, относительно которых рассматривается движение и часы – это система отсчета.
Простым движением является движение материальной точки. Материальной точкой может быть любое тело. В этом случае его размерами и формой пренебрегают. Движение материальной точки описывают уравнениями движения. Они показывают зависимость координаты от времени:
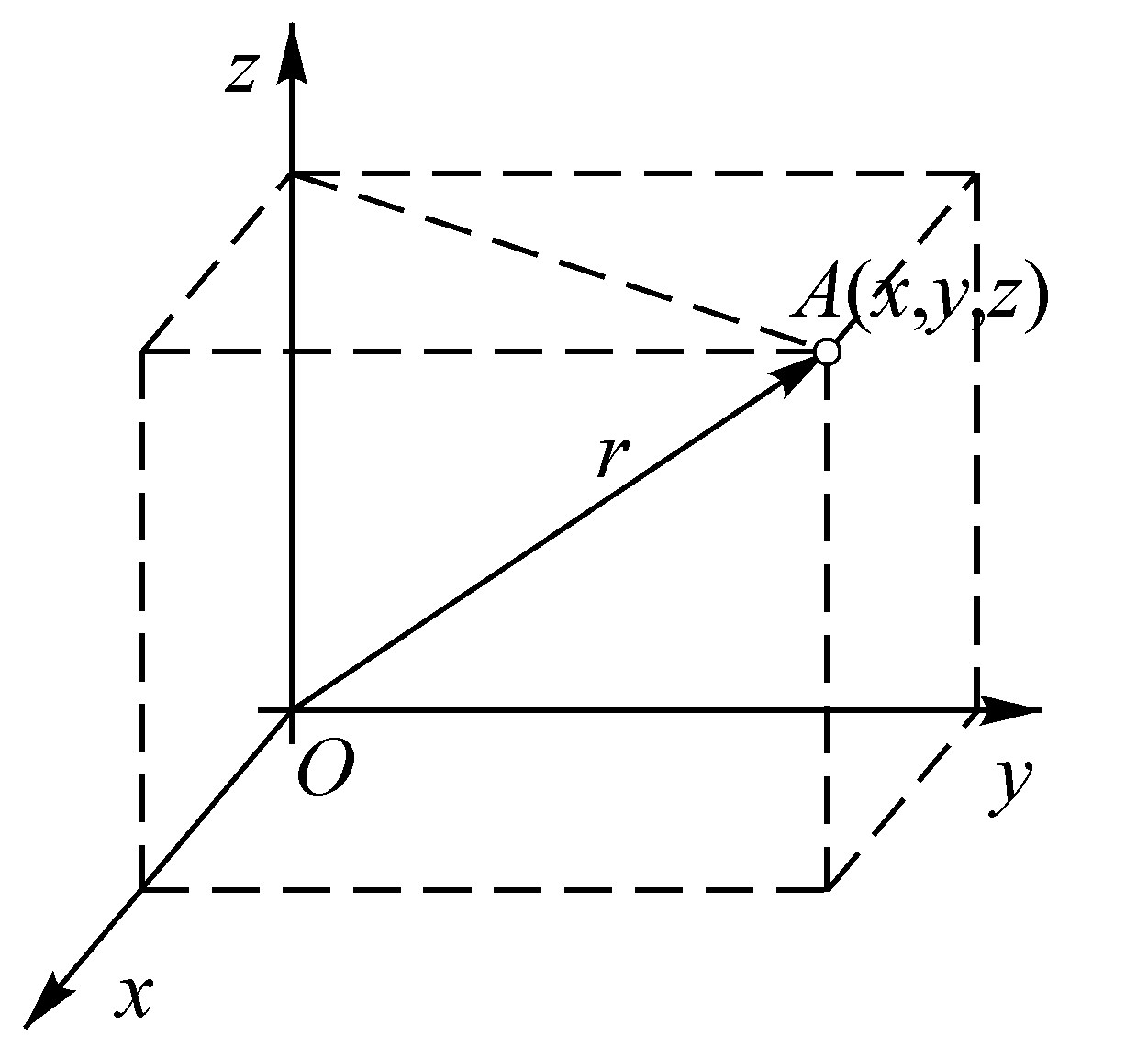 Рис. 1
Рис. 1
|
 ;
;  ;
;  .
.
Уравнения записаны для декартовой системы отсчета (рис. 1).
Из уравнений движения можно найти уравнение траектории. Для этого из уравнений нужно исключить время. Движение точки можно описать векторным уравнением.

Поступательное движение. Это движение, при котором любая прямая, связанная с движущимся телом, остается параллельной самой себе.
Вращательное движение. В этом случае все точки тела движутся по окружностям, центры которых лежат на одной прямой. Эта прямая – ось вращения.
Траектория – это линия в пространстве, по которой движется материальная точка. Длина траектории – это путь. Путь измеряется в метрах [м].
Прямолинейное движение – это движение по прямой линии. Криволинейное движение – это движение по окружности.
Перемещение – это вектор, соединяющий начальное и конечное положение материальной точки при движении.
Принцип независимости движений: Если точка одновременно участвует в нескольких движениях, то результирующее перемещение точки равно векторной сумме перемещений, совершаемых ею за то же время в каждом из движений отдельно.
Линейная скорость
Скорость определяет быстроту изменения расстояния (пути), пройденного телом (материальной точкой), и направление движения. Скорость – это векторная величина. Вектор скорости направлен по касательной к траектории.
 Рис. 2
Рис. 2
|
 (рис. 2). Скорость при этом изменится только по направлению. Перенесем вектор
(рис. 2). Скорость при этом изменится только по направлению. Перенесем вектор  из точки N в точку M, тогда вектор
из точки N в точку M, тогда вектор 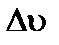 характеризует изменение скорости по направлению. Средняя скорость
характеризует изменение скорости по направлению. Средняя скорость  ; Если время
; Если время  , то получим значение мгновенной скорости
, то получим значение мгновенной скорости
 ;
;
Численное значение мгновенной скорости материальной точки равно первой производной от пути по времени. Скорость измеряется в метрах на секунду [м/с].
При движении с постоянной скоростью путь
 Рис. 3
Рис. 3
|
 .
.
При движении с переменной скоростью
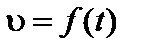 .
.
Путь можно найти из соотношения:

Графически численное значение пути можно найти через площадь под зависимостью  (рис. 3).
(рис. 3).
Если материальная точка участвует в нескольких движениях одновременно, то в соответствии с принципом независимости движений скорость результирующего движения равна векторной сумме скоростей всех движений, в которых участвует точка.
Ускорение
 Рис. 4
Рис. 4
|
Рассмотрим переход материальной точки из положения М в N (рис. 4) за малое время  . Вектор
. Вектор  перенесем в положение M. Тогда вектор
перенесем в положение M. Тогда вектор  характеризует полное изменение скорости. Вектор
характеризует полное изменение скорости. Вектор  представим суммой векторов
представим суммой векторов  и
и  . Вектор
. Вектор  показывает изменение скорости по величине, а вектор
показывает изменение скорости по величине, а вектор  – по направлению.
– по направлению.
Среднее полное ускорение материальной точки
 .
.
Мгновенное ускорение материальной точки при 
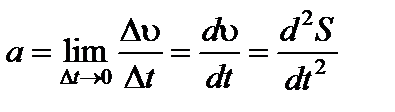 .
.
Таким образом, полное ускорение материальной точки равно первой производной от скорости по времени или второй производной от пути по времени. Ускорение измеряется в метрах на секунду во второй степени [м/с2].
Найдем  . При
. При  вектор
вектор  стремится стать касательной. Обозначим вектор
стремится стать касательной. Обозначим вектор  тогда
тогда

Величина  – называется касательным ускорением и определяет быстроту изменения скорости по величине. Обозначим вектор
– называется касательным ускорением и определяет быстроту изменения скорости по величине. Обозначим вектор  .
.
Найдем 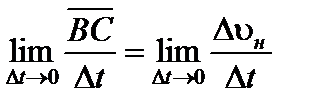 .
.
Из рис. 3  ;
;  .
.
 ;
;
Тогда 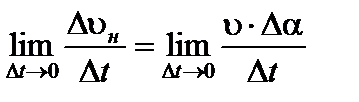 ;
;
Умножим на 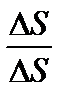 и примем во внимание, что
и примем во внимание, что


 Рис. 5
Рис. 5
|
 – называется нормальным ускорением и характеризует быстроту изменения скорости по направлению.
– называется нормальным ускорением и характеризует быстроту изменения скорости по направлению.
На рис. 5. показана связь ускорений a,  и
и  при движении по траектории MN.
при движении по траектории MN.
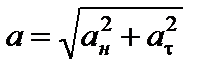 .
.
Динамика. Законы Ньютона. Импульс тела
1. В динамике движение тела рассматривается с учетом причин, вызывающих движение. Такими причинами являются различные взаимодействия. Мерой взаимодействия является величина, называемая силой. Сила – векторная величина. Основная задача динамики – написать уравнение движения.
Важным понятием в динамики является масса. Масса – это характеристика тела. Масса связывает между собой силу, действующую на тело, и ускорение, с которым тело будет двигаться. Если на тело последовательно действуют силы F 1, F 2, F 3 …, а соответствующие им ускорения тела a 1, a 2, a 3 …, то
 – масса тела. Масса тела измеряется в килограммах [кг].
– масса тела. Масса тела измеряется в килограммах [кг].
Первый закон Ньютона. Тело сохраняет состояние покоя или прямолинейного равномерного движения до тех пор, пока на него не действуют другие тела. Чем больше масса тела, тем труднее перевести его из одного состояния в другое. Масса тела является мерой его инертности. Состояния покоя и равномерного прямолинейного движения равноценны. Системы отсчета, соответствующие первому закону Ньютона, называются инерциальными.
Второй закон Ньютона. Ускорение, с которым движется тело, пропорционально силе, действующей на тело и обратно пропорционально массе этого тела:
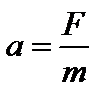
Следствие из второго закона:  называется уравнением движения тела.
называется уравнением движения тела.  ‑ это векторная сумма всех сил, действующих на тело. Каждая из этих сил сообщает телу ускорение, так как если бы других сил не было. Это принцип независимости действия сил.
‑ это векторная сумма всех сил, действующих на тело. Каждая из этих сил сообщает телу ускорение, так как если бы других сил не было. Это принцип независимости действия сил.
Третий закон Ньютона. При взаимодействии двух тел сила, действующая на первое тело со стороны второго, равна по величине и противоположна по направлению силе, действующей на второе тело со стороны первого:

Силы  и
и  приложены к разным телам.
приложены к разным телам.
2. Из второго закона Ньютона следует понятие импульса тела. Запишем второй закон Ньютона  . Преобразуем его
. Преобразуем его
 ;
;  ;
;  ;
;  .
.
 ‑ называется импульсом тела;
‑ называется импульсом тела;  – импульс силы. Импульс – векторная величина. Единица измерения импульса [кг∙м/с].
– импульс силы. Импульс – векторная величина. Единица измерения импульса [кг∙м/с].
Система тел называется изолированной (замкнутой), если для каждого тела системы все силы со стороны тел, внешних по отношению к данной системе, уравновешены или отсутствуют. Докажем это. В изолированной системе тел суммарный импульс тел с течением времени не изменяется – это закон сохранения импульса.
Пусть в изолированной системе находится n тел, mi – масса i -го тела;  – скорость i -го тела. Тогда по второму закону Ньютона запишем для n тел,
– скорость i -го тела. Тогда по второму закону Ньютона запишем для n тел,

Эти уравнения почленно суммируем и попарно группируем силы Fik и Fki.
 .
.
По третьему закону Ньютона правая часть уравнения равна нулю.

Нулю равна производная от постоянной величины.
Значит  , т.е. импульс замкнутой системы с течением времени не изменяется.
, т.е. импульс замкнутой системы с течением времени не изменяется.
Силы в механике
1) Силы упругости. Закон Гука.
При деформации тела под нагрузкой его частицы смещаются. Если смещение небольшое, то после прекращения действия нагрузки частицы возвращаются в исходное состояние. Это упругая деформация. При этом в теле возникают по третьему закону Ньютона силы противодействия. Это силы упругости  . Силы измеряются в Ньютонах [Н].
. Силы измеряются в Ньютонах [Н].
Если частицы тела после прекращения действия нагрузки не возвращаются в исходное состояние, деформацию называют пластической.
Величина  называется механическим напряжением. Здесь S – площадь сечения тела, на которое действует
называется механическим напряжением. Здесь S – площадь сечения тела, на которое действует 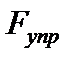 . Единица измерения напряжения Паскаль [Н/м2 = Па].
. Единица измерения напряжения Паскаль [Н/м2 = Па].
 ;
;  – это напряжение называется нормальным;
– это напряжение называется нормальным;
 || S;
|| S;  – это напряжение называется касательным.
– это напряжение называется касательным.
Англичанин Р. Гук установил, что упруго деформируя тело различными силами F, получаем при этом различные по величине деформации Δ x:
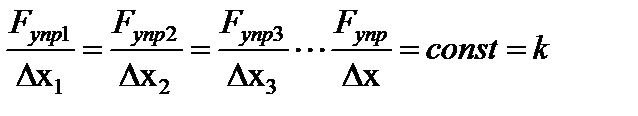 – коэффициент жесткости тела. k – это характеристика тела. Единицы измерения [Н/м].
– коэффициент жесткости тела. k – это характеристика тела. Единицы измерения [Н/м].
 Рис. 6
Рис. 6
|
 . Отношение
. Отношение  – называется относительной деформацией, и закон Р. Гука имеет вид
– называется относительной деформацией, и закон Р. Гука имеет вид  ; E – это коэффициент жесткости, называемый модулем нормальной упругости или модулем Юнга.
; E – это коэффициент жесткости, называемый модулем нормальной упругости или модулем Юнга.
Величина  – называется коэффициентом Пуассона.
– называется коэффициентом Пуассона.
Запишем закон Р. Гука для деформации сдвигом (рис. 7).
 Рис. 7
Рис. 7
|
 можно записать
можно записать
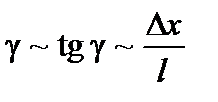 – относительная деформация.
– относительная деформация.
Закон Р. Гука примет вид 
здесь G – модуль сдвига (коэффициент жесткости при сдвиге).
2) Силы трения.
Всякое тело при движении встречает сопротивление окружающей среды. Силы сопротивления называют силами трения. Различают: внутреннее трение (вязкость) – здесь силы трения препятствуют перемещению одних слоев тела относительно других; внешнее трение – здесь силы трения препятствуют перемещению относительно друг друга двух соприкасающихся тел.
а) Статическое трение (внешнее). Тело лежит на горизонтальной плоскости (рис. 8).
 Рис. 8
Рис. 8
|
 численно равна силе
численно равна силе  , при которой тело начнет двигаться по плоскости с исчезающе малой скоростью. Значение силы трения определяется из выражения:
, при которой тело начнет двигаться по плоскости с исчезающе малой скоростью. Значение силы трения определяется из выражения:
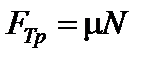
здесь  – коэффициент трения;
– коэффициент трения;  – сила реакции опоры. В соответствии с первым законом Ньютона сумма сил в вертикальном направлении равна нулю, т.е.
– сила реакции опоры. В соответствии с первым законом Ньютона сумма сил в вертикальном направлении равна нулю, т.е.
 .
.
б) Вязкое трение (внутреннее).
Силы вязкого трения зависят от скорости  движения тела в среде. При малых скоростях
движения тела в среде. При малых скоростях  , а при больших
, а при больших  . Здесь
. Здесь  и
и  – коэффициенты, зависящие от свойств среды и формы тела.
– коэффициенты, зависящие от свойств среды и формы тела.
3) Сила тяжести. Закон всемирного тяготения.
Все тела в природе взаимно притягивают друг друга. Сила притяжения определяется из выражения, полученного И. Ньютоном.
 ;
;
 – гравитационная постоянная
– гравитационная постоянная  ;
;  и
и  – массы взаимодействующих тел; r – расстояние между центрами тяжести тел. Сила
– массы взаимодействующих тел; r – расстояние между центрами тяжести тел. Сила  направлена вдоль прямой, проходящей через центры тяжести тел.
направлена вдоль прямой, проходящей через центры тяжести тел.
Силу притяжения тела массой m к Земле с массой  запишем в виде
запишем в виде  ,
,
где  – радиус Земли (размер тела <<
– радиус Земли (размер тела <<  ).
).
Введем обозначение:  .
.
Величина g имеет размерность ускорения. g называют ускорением земного притяжения или ускорением свободного падения. В итоге сила притяжения к Земле или сила тяжести

Если тело поднято над Землей на высоту H, то сила тяжести:
 ;
;  ;
;
4) Вес тела.
Весом тела называется сила, с которой тело действует на опору или подвес. Вес тела зависит от условий, в которых его определяют.
 Рис. 9
Рис. 9
|
 и сила реакции опоры N. Реакция опоры N это противодействие опоры действию тела P – весу тела. Но по третьему закону Ньютона
и сила реакции опоры N. Реакция опоры N это противодействие опоры действию тела P – весу тела. Но по третьему закону Ньютона 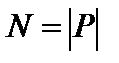 ;
;
При определении веса тела обычно находят реакцию опоры N.
Найдем сумму проекций сил на ось Х:  (1 закон Ньютона, тело в покое).
(1 закон Ньютона, тело в покое).

т.е. на покоящейся горизонтальной поверхности вес тела равен действующей на него силе тяжести.
 Рис. 10
Рис. 10
|
 ;
;
 Рис. 11
Рис. 11
|
в) Это же тело находится в лифте (рис. 11). Лифт движется вертикально вверх с ускорением а. Запишем для тела массой m уравнение движения (следствие второго закона Ньютона).


 .
.
Вес тела возрос в сравнении с п. а).
 Рис. 12
Рис. 12
|
 ;
;  ;
;
Вес тела уменьшился. Если  , то вес тела в этом случае равен нулю. Такое состояние называется невесомостью. Масса при этом не исчезает.
, то вес тела в этом случае равен нулю. Такое состояние называется невесомостью. Масса при этом не исчезает.
Энергия и работа
1) Единой мерой различных форм движения является энергия (W). Энергия – это запас возможности совершить работу (A). Процесс изменения энергии – это процесс совершения работы. Работа, совершаемая постоянной силой F, определяется формулой:

Здесь 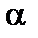 – угол между направлением действия силы F и направлением перемещения на пути S. Работа и энергия измеряются в Джоулях [Дж].
– угол между направлением действия силы F и направлением перемещения на пути S. Работа и энергия измеряются в Джоулях [Дж].
Полная работа, совершаемая переменной силой F (S) на пути от 0 до S, определится интегрированием выражения

Здесь  – элементарная работа на участке пути
– элементарная работа на участке пути  .
.
 ;
;
 Рис. 13
Рис. 13
|
 .
.
Для характеристики скорости совершения работы вводится понятие мощности ( ):
):
 ;
;
Здесь t – время. Единица измерения мощности ватт [Вт].
2) Кинетическая энергия.
Кинетическая энергия – это механическая энергия всякого движущегося тела. Измеряется кинетическая энергия работой, которую может совершить тело при его торможении до полной остановки. На малом участке пути переменная сила совершит работу:
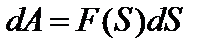 .
.
По второму закону Ньютона силу можно найти


Тогда 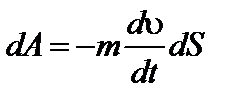 ; Полная работа
; Полная работа
 ;
;
 ‑ кинетическая энергия.
‑ кинетическая энергия.
3) Потенциальная энергия.
 Рис. 14
Рис. 14
|
 при подъёме с постоянной скоростью.
при подъёме с постоянной скоростью.

Тогда  ;
;  ‑ потенциальная энергия. Это также механическая форма энергии.
‑ потенциальная энергия. Это также механическая форма энергии.
Поднимем тело на высоту H по пути l (рис. 14).
 но
но  . Тогда
. Тогда  .
.
Силы (в данном случае это сила тяжести), работа которых не зависит от формы пути, называются консервативными.
б) Потенциальная энергия упруго деформированного тела.
Из закона Р. Гука  ; По третьему закону Ньютона внешняя сила
; По третьему закону Ньютона внешняя сила  . Для нее
. Для нее  . Найдем работу, совершаемую этой силой при упругой деформации тела на величину
. Найдем работу, совершаемую этой силой при упругой деформации тела на величину  .
.
 ;
; 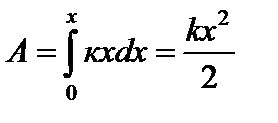 ;
; 
Здесь  – потенциальная энергия, запасенная в упруго деформированном теле.
– потенциальная энергия, запасенная в упруго деформированном теле.
Одним из основных фундаментальных законов в физике является закон сохранения и превращения энергии.
В замкнутой системе энергия может переходить из одних видов в другие и передаваться от одного тела к другому, но её общее количество остается неизменным.
Если в замкнутой системе сохраняется только механическая энергия  , система называется консервативной.
, система называется консервативной.
Если механическая энергия постепенно уменьшается за счет перехода в другие (немеханические) формы энергии, система называется диссипативной.
Date: 2016-05-25; view: 798; Нарушение авторских прав