Основні теоретичні відомості. Сигнали, що надходять від джерела повідомлень (мікрофона, телекамери, датчика телеметричної системи) не можуть бути безпосередньо передані по радіоканалу

Сигнали, що надходять від джерела повідомлень (мікрофона, телекамери, датчика телеметричної системи) не можуть бути безпосередньо передані по радіоканалу. Основна причина цього факту полягає у відносно низькій частоті цих сигналів. Щоб здійснити ефективну передачу сигналів у якому-небудь середовищі необхідно перенести спектр цих сигналів в область досить високих частот. Дана процедура в радіотехніку здійснюється за допомогою модуляції.

Ідея способу, що дозволяє переносити спектр сигналу в область високих частот, полягає в наступному.

У передавачі формується допоміжний високочастотний сигнал, який називається несучим коливанням. Нехай 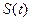– низькочастотне повідомлення (сигнал), що потребує передачі по радіоканалу. Якщо, принаймні, один з параметрів несучого коливання змінюється в часі пропорційно переданому повідомленню, то несуче коливання несе в собі інформацію, укладену в .

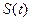Фізичний процес управління параметрами несучого коливання з метою передачі корисного повідомлення називається модуляцією.

У радіотехніці широке розповсюдження одержали системи, що використовують в якості несучого коливання простий гармонічний сигнал, що має три інформаційних параметри: амплітуду, частоту та фазу. Змінюючи в часі один із цих параметрів за законом переданого повідомлення можна одержати різні види модуляції.

Якщо за законом переданого повідомлення змінюється амплітуда 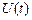сигналу, а інші два параметр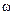и й 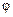залишаються незмінними, то така зміна несучого коливання називається амплітудною модуляцією.

Математична модель амплітудно-модульованого сигналу (АМ-сигналу) має вигляд:

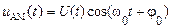. (4.1)

Осцилограма АМ-сигналу має характерний симетричний щодо осі часу вид (рис. 4.1). Відповідно до формули (4.1) АМ-сигнал являє собою добуток обвідної 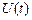й гармонічного заповнення 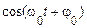. Огбвідна змінюється в часі значно повільніше, ніж високочастотне заповнення.

Рис. 4.1. АМ-сигнал і його обвідна

Зв'язок між обвідною 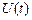й переданим повідомленням 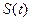визначається співвідношенням

, (4.2)

де 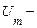постійне значення амплітуди несучого коливання під час відсутності модуляції; 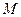– коефіцієнт амплітудної модуляції (глибина амплітудної модуляції).

Застосування АМ-сигналів з малою глибиною модуляції в радіотехніці недоцільно через неповне використання потужності передавача. У той же час, при значеннях виникає явище перемодуляції, коли форма обвідної перестає повторювати форму корисного повідомлення.

Найпростіший АМ-сигнал, який може бути отриманий при модуляції простим несучим низькочастотним гармонічним коливанням із частотою

, (4.3)

називається однотональним АМ-сигналом.

Використовуючи формулу добутку косинусів, з (4.3) можна записати

(4.4)

Вираз (4.4) установлює спектральний склад однотонального АМ-сигналу, що включає: коливання на несучій частоті 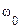, коливання на верхній боковій частоті й коливання на нижній боковій частоті . Амплітуди бокових спектральних складових рівні й розташовані симетрично щодо несучого коливання (рис. 4.2).

Рис. 4.2. Спектр АМ-сигнала

Джерело однотонального АМ-коливання може бути представлене трьома послідовно включеними джерелами гармонійних коливань:

,

,

.

Навіть при модуляції 100% (М = 1) частка потужності двох бокових складових дорівнює тільки 50% потужності несучого коливання. Оскільки корисна інформація укладена в бокових коливаннях, можна констатувати неефективність використання потужності при передачі АМ-сигналів. На практиці однотональні АМ-сигнали використовуються рідко. Модулюючи низькочастотні сигнали, що застосовуються в радіотехнічних системах різного призначення, мають складний спектральний склад. Математична модель таких сигналів описується сумою тригонометричних функцій

. (4.5)

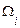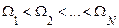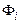Тут частоти утворять упорядковану зростаючу послідовність , а амплітуди й початкові фази є довільними.

Підставивши (4.5) в (4.3), отримаємо

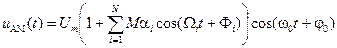. (4.6)

Уведемо сукупність парціальних (часткових) коефіцієнтів модуляції й запишемо аналітичний вираз для багатотонального АМ-сигналу у формі

. (4.7)

Спектральне розкладання цього сигналу виконується так само, як і для однотонального АМ-сигналу:

. (4.8)

У спектрі багатотонального АМ-сигналу (рис. 4.3), крім несучого коливання, містяться групи верхніх і нижніх бокових коливань.

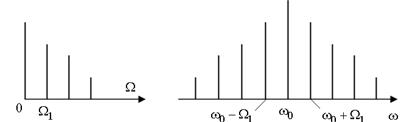
Рис. 4.3. Формування спектра багатотонального АМ-сигнала

Спектр верхніх бокових коливань є масштабною копією спектра модулюючого сигналу, зрушеною в область високих частот на величину 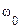. Спектр нижніх бокових коливань також повторює спектральну діаграму сигналу 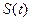, але розташовується дзеркально щодо несучої частоти .

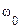Аналіз спектральної діаграми дозволяє зробити висновок: ширина спектра АМ-сигналу дорівнює подвоєному значенню найвищої частоти в спектрі низькочастотного модулюючого сигналу.

Для більш ефективного використання потужності передавача застосовуються АМ-сигнали з подавленим несучим коливанням, що реалізують так звану балансову амплітудну модуляцію.

На підставі формули (4.3) для АМ-сигналу з балансовою модуляцією отримаємо

Коливання тут виходять у результаті перемножування несучого й модулюючого сигналів. З фізичної точки зору вони являють собою биття двох гармонійних коливань із однаковими амплітудами й частотами, рівними верхнім і нижнім боковим частотам.

Більш продуктивне удосконалення АМ-сигналів пов'язане із придушенням верхньої або нижньої бокової смуги частот.

Сигнали з однією боковою смугою (ОБС) за зовнішніми характеристиками нагадують звичайні АМ-сигнали. Наприклад, однотональний ОБС-сигнал з подавленою нижньою боковою частотою має математичну модель виду:

Проведення тривіальних тригонометричних перетворень дозволяє одержати

.

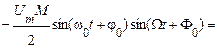
Два останні доданки являють собою добуток двох функцій, одна з яких змінюється в часі повільно, а друга – швидко. Беручи до уваги той факт, що «швидкі» співмножники перебувають по відношенню друг до друга у квадратурі, вираз для обвідної ОБС-сигналу, що повільно змінюється, буде мати вигляд:

.

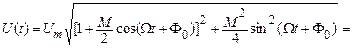
Основна перевага ОБС-сигналів полягає у дворазовому скороченні смуги займаних частот, що виявляється суттєвим для частотного ущільнення радіоканалів, особливо при організації зв'язку на коротких хвилях.

Нехай у несучому гармонічному коливанні за законом переданого повідомлення змінюється або частота 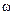, або початкова фаза 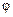, а амплітуда залишається незмінною. Оскільки аргумент гармонійного коливання , що називається повною фазою, визначає поточне значення фазового кута, такі сигнали одержали назву сигналів з кутовою модуляцією.

Припустимо, що повна фаза 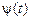пов'язана із сигналом залежністю

, (4.9)

де значення частоти під час відсутності модулюючого сигналу; деякий коефіцієнт пропорційності. Модуляція, яка описується виразом (4.9), називається фазовою модуляцією (ФМ). При цьому

. (4.10)

Математична модель ЧМ-сигналу

. (4.11)

Основним параметром ЧМ-сигналу є девіація частоти . Зовні часові діаграми ФМ-сигналів і ЧМ-сигналів не відрізняються. Однак, при їхньому формуванні є принципова різниця: фазовий зсув між ФМ-сигналом і немодульованим коливанням пропорційний , а для ЧМ-сигналу – цей зсув пропорційний інтегралу від .

У випадку однотонального ФМ-сигналу миттєва частота змінюється за законом , де девіація частоти. Повна фаза такого сигналу

,

де постійний фазовий кут.

Величина

(4.12)

називається індексом кутової модуляції, який являє собою девіацію фази сигналу, виражену в радіанах.

Якщо для простоти покласти, що постійні фазові кути , то миттєве значення ЧМ-сигналу має вигляд:

. (4.13)

Аналітична форма запису однотонального ФМ-сигналу буде аналогічною. Однак ЧМ-сигнали й ФМ-сигнали при зміні частоти модуляції й амплітуди модулюючого сигналу поводяться по-різному.

При ЧМ девіація частоти 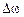пропорційна амплітуді модулюючого сигналу і не залежить від його частоти. При ФМ індекс модуляції пропорційний амплітуді модулюючого сигналу і не залежить від його частоти. Як наслідок цього, девіація частоти при ФМ лінійно зростає зі збільшенням частоти.

Для малих індексів модуляції у спектрі сигналу з кутовою модуляцією міститься несуче коливання й дві бокові смуги (верхня й нижня) на частотах і . Індекс грає тут таку ж роль, як коефіцієнт АМ. Суттєва відмінність спектральної діаграми сигналів з кутовою модуляцією від діаграми АМ-сигналу полягає в тому, що нижнє бокове коливання має додатковий фазовий зсув на .

У загальному випадку математична модель сигналу з кутовою модуляцією при будь-якому значенні індексу модуляції:

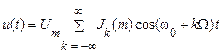. (4.14)

Тобто спектр однотонального сигналу з кутовою модуляцією містить нескінченну кількість складових, частоти яких рівні , а амплітуди – пропорційні значенням функції Беселя .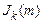

Практична ширина спектра сигналу з кутовою модуляцією:

. (4.15)

Для реальних сигналів з кутовою модуляцією, як правило, , тому

. (4.16)

Таким чином, сигнал з кутовою модуляцією займає смугу частот, приблизно рівну подвоєної девіації частоти.

Для передачі АМ-сигналу потрібна смуга частот , що у разів менше смуги ЧМ-сигналу й ФМ-сигналу. Широка смуга частот сигналів з кутовою модуляцією обумовлює їхнє використання тільки на дуже високих частотах, у діапазонах метрових і більш коротких хвиль. Однак саме широкосмуговість забезпечує виграш у завадостійкості ЧМ-сигналів і ФМ-сигналів у порівнянні з АМ-сигналами.

Якщо значення вибрати так, що , то отримаємо ЧМ-сигнал або ФМ-сигнал з подавленою несучої на частоті .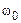

Date: 2016-05-25; view: 584; Нарушение авторских прав