Основні теоретичні відомості

Довільний періодичний сигнал може бути представлений у вигляді ряду Фур'є, перша тригонометрична форма запису якого:

, (2.1)

де коефіцієнти

,

,

,

.

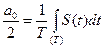Тут – постійна складова ряду Фур’є, та – амплітуди косинусної та синусної складових ряду Фур’є відповідно. Основна кругова частота або частота першої гармоніки однозначно визначається періодом сигналу. Цілі числа 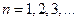– вказують на номер гармоніки.

З (2.1) слідує, що у загальному випадку періодичний сигнал містить у собі не залежну від часу постійну складову й нескінченний набір гармонійних коливань, так званих гармонік із частотами , кратними основній частоті послідовності.

З аналізу виразів для коефіцієнтів ряду Фур'є можна зробити висновок, що парний сигнал має тільки косинусоїдальні, а непарний – тільки синусоїдальні складові.

Будь-яка гармоніка ряду Фур'є характеризується амплітудою й початковою фазою . Для визначення їхніх значень коефіцієнти ряду (2.1) необхідно записати у вигляді

, ,

звідки

, .

Підставивши вирази для амплітуди й початкової фази в (2.1), отримаємо іншу, іноді більш зручну, форму запису ряду Фур'є

.(2.2)

.

Комплексна форма запису ряду Фур'є

. (2.3)

.

.

.

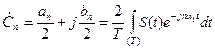Графічну побудову, що інтерпретує коефіцієнти ряду Фур'є, для конкретного сигналуназивають спектральною діаграмою сигналу. Розрізняють амплітудні (рис. 2.1, а) й фазові (рис. 2.1, б) діаграми. Залежність амплітуд гармонічних складових від частоти називають амплітудно-частотним спектром (АЧС) або спектральної діаграмою амплітуд. Залежність фаз гармонічних складових від частоти називають фазо-частотним спектром (ФЧС) або спектральної діаграмою фаз.

Рис. 2.1. Спектральні діаграми періодичного сигналу

На діаграмі по горизонтальній осі відкладені дискретні частоти гармонік, а по вертикальній осі – значення амплітуд і початкових фаз цих гармонік. Спектри періодичних сигналів є дискретними, лінійчатими.

У цій роботі буде досліджуватись сигнал, представлений на рис. 2.2.

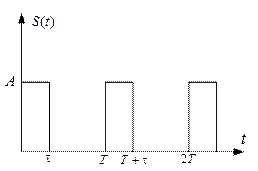
Рис. 2.2. Послідовність прямокутних імпульсів

Запишемо необхідні коефіцієнти ряду Фур'є

.

Після підстановки цих коефіцієнтів в (2.1) маємо

, (2.4)

де – шпаруватість періодичної послідовності.

При цьому

.

Під час порівняння АЧС для зміни тривалості імпульсів періодичної послідовності прямокутних відеоімпульсів необхідно звернути увагу на наступні закономірності:

1. Форма обвідної АЧС лишається незмінною, оскільки незмінною лишається форма імпульсу (прямокутна).

2. Частоти гармонік лишаються незмінними, оскільки вони залежать лише від періоду слідування імпульсів.

3. Ширина спектру сигналу змінюється – зі збільшенням тривалості імпульсу вона зменшується (оскільки ).

4. Зі збільшенням тривалості імпульсу зменшується шпаруватість та збільшується постійна складова.

5. Зі збільшенням тривалості імпульсу зменшується число гармонік у смузі частот, яку займає спектр сигналу, та змінюється відношення між амплітудами сусідніх гармонік – збільшується різниця амплітуд.

Під час порівняння АЧС для зміни періоду (частоти) імпульсів періодичної послідовності прямокутних відеоімпульсів необхідно звернути увагу на наступні закономірності:

1. Форма обвідної АЧС лишається незмінною, оскільки незмінною лишається форма імпульсу (прямокутна).

2. Ширина спектру сигналу лишається незмінною, оскільки вони визначається лише тривалістю імпульсів.

3. Змінюється основна частота гармонік в спектрі – під час зменшення періоду вона збільшується.

4. Зі збільшенням періоду збільшується шпаруватість та зменшується постійна складова.

5. Зі збільшенням періоду імпульсів зменшується число гармонік у смузі частот, яку займає спектр сигналу, та змінюється відношення між амплітудами сусідніх гармонік – збільшується різниця амплітуд.

Date: 2016-05-25; view: 443; Нарушение авторских прав