Показатели центра распределения и структурные характеристики вариационного ряда

Для характеристики среднего значения признака в вариационном ряду используются так называемые показатели центра распределения. К ним относятся средняя величина признака, мода и медиана.

Расчет средней величины признака () в вариационном ряду осуществляется по формуле средней арифметической взвешенной:

где х — варианты признака;
f — частоты (частости).

При расчете средней величины интервального ряда в качестве вари­антов признака используются значения середины интервалов (гр. 5, табл. 4.1). Для нахождения середины открытых интервалов (в нашем примере это первая и последняя группы) необходимо их предварительно условно закрыть, т.е. определить недостающую верхнюю и нижнюю границы. Принято считать, что в первой группе величина интервала равна интервалу второй группы, а в последней — интервалу предыдущей. В рассматриваемом примере используется ряд с равными интервалами, величина которых 0,5 тыс. руб. Тогда условная нижняя граница первого интервала будет равна: 0,5 тыс. руб. – 0,5 тыс. руб. = 0, а середина — 0,25 тыс. руб., условная верхняя граница последнего интервала: 3,0 тыс. руб. + 0,5 тыс. руб. = 3,5 тыс. руб., а середина — 3,25 тыс. руб.

Осуществим расчет средней величины месячного среднедушевого денежного дохода (), используя в качестве весов частоты распределения (f). Промежуточные расчеты запишем в гр. 6 табл. 4.1. Тогда

= 1,82 тыс. руб.

Месячный среднедушевой доход составляет 1820 руб.

Можно при расчете средней величины в качестве весов использовать частости распределения (ω) (промежуточные расчеты в гр. 7 табл. 4.1). Величина средней от этого не меняется.

= 1,82 тыс. руб.

Мода — значение признака, наиболее часто встречающееся в изучаемой совокупности. В дискретном ряду модой является вариант с наибольшей частотой (частостью). В интервальном вариационном ряду мода рассчитывается по формуле:

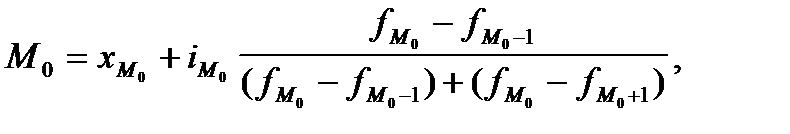
где —нижняя граница модального интервала;

— -величина модального интервала;

—частоты (частости) соответственно модального, домодального и послемодального интервалов.

Модальный интервал — это интервал, имеющий наибольшую частоту (частость). В нашем примере это третий интервал — от 1,0 до 1,5 тыс. руб.

Рассчитаем модальное значение признака, используя в качестве весов частости распределения:

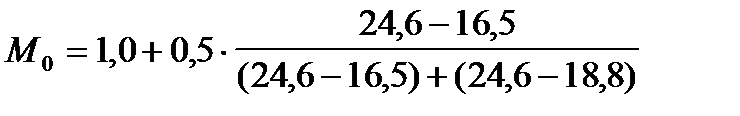= 1,29 тыс. руб.

Таким образом, в нашем примере наиболее часто встречающаяся величина среднедушевого дохода составляет 1 290 руб.

Расчет моды с использованием в качестве весов частот распределения даст аналогичный результат:

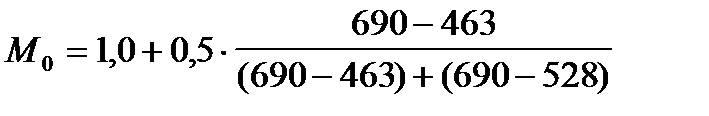= 1,29 тыс. руб.

Отметим, что вычисление моды в интервальном ряду является весьма условным.

Приближенно модальное значение признака можно определить и графически — по гистограмме. Для этого нужно взять столбец, имеющий наибольшую высоту, и из его левого верхнего угла провести отрезок в верхний угол последующего столбца, а из правого угла — в верхний правый угол предыдущего (см. рис. 4.1). Абсцисса точки пересечения отрезков и будет соответствовать модальному значению признака в изучаемой совокупности.

Медиана — вариант, расположенный в середине упорядоченного вариационного ряда, делящий его на две равные части, таким обра­зом, что половина единиц совокупности имеют значения признака меньше, чем медиана, а половина — больше, чем медиана. В интервальном ряду медиана определяется по формуле:

,

где х_Me — начало медианного интервала; i_Me - величина медианного интервала;

— сумма частот (частостей) вариационного ряда;

f_M — - частота (частость) медианного интервала;

— сумма накопленных частот (частостей) в домедианном интервале.

Медианный интервал — это интервал, в котором находится поряд­ковый номер медианы. Для его определения необходимо подсчитать сумму накопленных частот (частостей) до числа, превышающего половину объема совокупности. По данным гр. 4 табл. 4.1 находим интервал, сумма накопленных частот в котором превышает 50 %. Это интервал от 1,5 до 2,0 тыс. руб. (S = 60,8 %), он и является медианным. Тогда

=1,72 тыс. руб.

Следовательно, половина жителей города в нашем примере имеет месячный среднедушевой доход меньше 1 720 руб., а половина — больше этой суммы.

Расчет медианного значения по частостям распределения даст аналогичный результат:

= 1,72 тыс. руб.,

где 1 179 —сумма накопленных частот в домедианном интервале.

Медиану приближенно можно определить графически — по кумуляте. Для этого высоту наибольшей ординаты, которая соответствует общей численности совокупности, делят пополам. Через полученную точку проводят прямую, параллельную оси абсцисс, до пересечения ее с кумулятой. Абсцисса точки пересечения и является медианой (см. рис. 4.3).

Расчет модального и медианного значений для вариационных рядов с неравными интервалами осуществляется по формулам, аналогичным приведенным выше, только вместо показателей частот (частостей) используются показатели абсолютной или относительной плотности распределения, которые обеспечивают сопоставимость неравных интервалов. Показатели плотности распределения находятся как отношения частот (частостей) к величине интервала:

– абсолютная плотность распределения

,

– относительная плотность распределения

,

где i — величина интервала.

По соотношению характеристик центра распределения (средней величины, моды и медианы) можно судить о симметричности эмпирического ряда распределения. Симметричным является распределение, в котором частоты двух вариантов, равностоящих в обе стороны от центра распределения, равны между собой. В симметричном распределении средняя величина, медиана и мода равны между собой:

Если > M_e > M₀, то имеет место правосторонняя асимметрия, т.е. большая часть единиц совокупности имеет значения изучаемого признака, превышающие модальное значение. На графике распределения правая ветвь относительно максимальной ординаты вытянута больше, чем левая.

Соотношение < M_e < M_o характерно для левосторонней асимметрии, при которой большая часть единиц совокупности имеет значения признака ниже модального. На графике распределения левая ветвь вытянута больше, чем правая.

Нашему примеру соответствует соотношение > M_e > M_o (1820 руб. > 1720 руб. > 1290 руб.), характерное для правосторонней асимметрии, что подтверждается графиками — гистограммой и полигоном распределения (см. рис. 4.1 и 4.2. Наличие правосторонней асимметрии свидетельствует о том, что большая часть жителей города имела месячный среднедушевой доход выше, чем его модальное значение (1 290 руб.).

При анализе вариационного ряда важно знать не только направление асимметрии (правосторонняя или левосторонняя), но и ее степень, которая измеряется с помощью коэффициентов асимметрии.

Моду и медиану называют еще структурными средними, поскольку они дают количественную характеристику структуры строения ва­риационных рядов. К структурным характеристикам относятся и другие порядковые статистики: квартили — делящие, ряд на 4 равные части, децили — делящие ряд на 10 частей, перцинтили — на 100 частей и др.

Date: 2016-05-25; view: 919; Нарушение авторских прав