Понятие о линейных цепях постоянного тока

Основные понятия и законы линейных электрических цепей постоянного тока
Для анализа и расчёта реальное электромагнитное устройство с происходящими в нём процессами заменяется некоторым расчётным эквивалентом – электрической цепью.

Фактически изучаются не реальные устройства, а их эквиваленты, которые, с определённой степенью точности, являются отражением их реальных свойств.

Электрическая цепь – это совокупность соединённых друг с другом источников энергии и нагрузок, по которым может протекать электрический ток.

Изображение электрической цепи называется схемой замещения электрической цепи или просто электрической схемой.
Рассмотрим характерные участки цепи:
- Ветвь – участок электрической цепи, в котором ток имеет одно и то же значение. Элементы ветви соединены между собой последовательно;
- Узел – место соединения трёх или более ветвей;

Место соединения ветвей обозначается точкой (обязательно – если ветви пересекаются).
- Контур – любой замкнутый путь в цепи.
Например, в схеме на рисунке 1.1, пять ветвей, три узла, шесть контуров. Убедитесь в этом самостоятельно, проверьте себя.

^ Закон Ома. Сопротивление и проводимость
Вспомните хорошо известные из школьного курса физики понятия.

Электрический ток (или сила тока) - количество заряда, проходящего через поперечное сечение проводника в единицу времени или производная заряда по времени i(t) = dq/dt.

Единица измерения тока – Ампер – А = Кл/с

Для цепей постоянного тока i(t) = const = I

Напряжение – разность электрических потенциалов между двумя точками цепи u(t) = φ₁ - φ₂.

В цепях постоянного тока u(t) = const = U.

Единица измерения напряжения – Вольт (В).
Одной из основных характеристик элемента цепи является зависимость тока от напряжения I = f (U), называемая вольт-амперная характеристика (ВАХ). Пример графиков двух ВАХ показан на рисунке 1.2.

ВАХ бывают линейные (если график – прямая линия) и нелинейные. На рисунке 1.2 характеристики 1 и 3 – линейные, а 2 – нелинейная. Соответственно, элементы цепи с линейной ВАХ называются линейными, а с нелинейной – нелинейными.
Линейная цепь - это цепь, состоящая только из линейных элементов. Если хотя бы один элемент цепи имеет нелинейную ВАХ, то цепь уже является нелинейной.

Важным параметром элемента цепи является его сопротивление R – коэффициент пропорциональности между током и напряжением.
В линейной цепи сопротивление элемента при любом напряжении постоянно и не зависит ни от напряжения, ни от тока. Зависимость тока от напряжения определяется законом Ома:
U = IR, где R = const.
Сопротивление R легко определить по графику ВАХ по любым двум точкам. R = ΔU/ΔI.

Определите: на какой из линейных ВАХ на рисунке 2 сопротивление больше: 1 или 3?

В нелинейной цепи сопротивление в каждой точке ВАХ различно. В данном разделе будем рассматривать только более простые, линейные цепи. Нелинейные цепи будут рассматриваться в последующих главах.
Сопротивление R является характеристикой проводника и определяется следующим образом:

R = 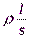, где l – длина проводника, ρ – удельное сопротивление, характеризующее материал проводника, S – площадь поперечного сечения.

Теоретически любой элемент цепи обладает сопротивлением, но на практике в расчётах цепь идеализируется, и сопротивлением проводов пренебрегают и считают, что всё сопротивление заключается в нагрузках.

Элемент цепи, обладающий сопротивлением, называют резистором, на схеме обозначается так:

Размеры резистора – 4х10.
Часто удобно использовать величину, обратную сопротивлению, и называемую проводимость G.
G = 1/R

Единицей проводимости называется Сименс (См).

1 См = 1/1 Ом.

Закон Ома в этом случае выглядит: I = GU

G = , где γ = 1/ ρ – удельная проводимость.

Рассмотрим участок ветви с резистором R (смотреть рисунок 1.3) и полярности величин.

Очевидно, всегда R > 0

U_ab = φ_a - φ_b

Если φ_a > φ_b то U_ab > 0 – напряжение положительно.

Ток считается положительным, если направление тока совпадает с направлением положительного напряжения и отрицательным, если его направление противоположно направлению положительного напряжения.
Рассмотрим теперь источник ЭДС (рисунок 1.4)

Стрелка источника ЭДС показывает направление положительного тока, который вызывает источник. Интересно, что направление напряжения на самом источнике ЭДС противоположно току.

Рассмотрим участок ветви, содержащий источник ЭДС и резистор (рисунок 1.5).

Некоторые студенты испытывают затруднения при анализе данной цепи. При данном направлении ЭДС, правильная формула:
U_ab = U_R – E = IR – E
Проанализируйте схему и запишите самостоятельно формулы при различных вариантах направлений напряжений, токов и источника.

^ Соединение сопротивлений
Во многих случаях расчёт электрической цепи можно упростить, путём преобразования её из сложного вида в более простой. При этом уменьшается число узлов, ветвей либо и то и другое.

Необходимое условие преобразования: токи и напряжения в остальных частях схемы, не подвергающихся преобразованию, не изменяются. Такое преобразование называется эквивалентным.
а) Последовательное соединение сопротивлений
Последовательное соединение – это такое, при котором во всех элементах цепи течёт одинаковый ток. Элементы ветви соединены последовательно (рис. 1.6).

Такую ветвь можно заменить одним резистором с сопротивлением R_экв, равным сумме сопротивлений всех резисторов.

R_экв = = R₁+R₂+R₃+…+R_n

Эквивалентное сопротивление при таком соединении всегда больше сопротивления любого из элементов. Если все сопротивления равны

R₁= R₂= R₃=…= R, то R_экв = nR

Для проводимостей G формула будет выглядеть так:

Напряжение на зажимах ab равно сумме напряжений на каждом элементе ветви.

б) Параллельное соединение сопротивлений
Параллельное соединение сопротивлений – это такое соединение, при котором ко всем элементам цепи приложено одинаковое напряжение.

Параллельно соединены элементы между двумя узлами (рисунок 1.7).

Ток I в неразветвлённой части равен сумме токов в каждом элементе.

I = I₁= I₂+ I₃+…+ I_n
Эквивалентная проводимость в этом случае равна сумме проводимостей всех элементов:

G_экв = = G₁+ G₂+ G₃+…+ G_n

Для сопротивлений R формула будет выглядеть так:

Как видите, формулы симметричны: при последовательном соединении складываются сопротивления, а при параллельном – проводимости.

Эквивалентное сопротивление при таком соединении всегда меньше сопротивления любого из элементов.

Если все сопротивления равны R₁= R₂= R₃=…= R, то

R_экв = R/n
Ток в любой ветви пропорционален проводимости этой ветви.
в) Смешанное соединение сопротивлений
Смешанное соединение сопротивлений – это такое соединение, которое можно представить в виде параллельного и последовательного.

На первый взгляд кажется, что любую схему соединения элементов можно представить в виде смешанного соединения и найти эквивалентное сопротивление путём преобразования параллельных и последовательных участков. Однако бывают случаи, когда соединение элементов не является смешанным. Примером такого случая может служить распространённая в электронике мостовая схема, показанная на рисунке 1.8.

Как найти сопротивление между точками a и d? После нескольких попыток упростить схему, легко убедиться, что здесь нет участков ни с последовательным, ни с параллельным соединением. Для этого нужно применить преобразование, описанное в следующем параграфе.

г) Преобразование «Звезда-треугольник»
Существует возможность эквивалентного преобра-зования треугольника сопротивлений, показанного на рисунке 1.9, в трёхлучевую звезду (рисунок 1.10).
При преобразовании одной схемы в другую, напряжения и токи, как при любом эквивалентном преобразовании, не изменяются.

Формулы для преобразования из треугольника в звезду:

Формулы для преобразования из звезды в треугольник:

R_ab = R_a+ R_b+ R_aR_b/R_с

R_ac = R_a+ R_c+ R_aR_c/R_b

R_bc = R_c+ R_b+ R_cR_b/R_a
Если все сопротивления равны, то легко убедиться, что сопротивления в треугольнике в три раза больше, чем в звезде.

Теперь вернёмся к мостовой схеме на рисунке 8. Можно преобразовать в ней треугольник abc в звезду. Получим схему на рисунке 1.11.

В этой схеме сопротивления треугольника R₁, R₂, R₃ преобразованы в звезду R_a, R_b, R_c.

Теперь не вызывает затруднения найти сопротивление R_ad. Для этого нужно найти последовательные соединения Rb-R4 и Rc-R5, затем параллельное соединение двух получившихся и затем - последовательное соединение с R_a.

Также и в других подобных случаях преобразование «звезда-треугольник» может быть незаменимым.
^ Источник ЭДС и источник тока
Источник энергии представляет собой источник ЭДС, имеющий внутреннее сопротивление r. К клеммам источника подключена нагрузка сопротивлением R. Источник ЭДС также называется: источник напряжения или генератор.

Схема источника энергии и подключённая к ней нагрузка показаны на рисунке 1.12. Она хорошо известна из курса физики средней школы.

В соответствии с законом Ома для полной цепи:
E = I (R+r) = IR + Ir = U + Ir

I = E/(R+r)
Напряжение на нагрузке U меньше напряжения ЭДС Е на величину Ir. Таким образом, на внутреннем сопро-тивлении r теряется полезная мощность.
Важными являются два состояния цепи.

1)R→ ∞ => I=0=>U=E– режим холостого хода (ХХ).

2)R→0 => U = 0, I = Е/r = I_кз – режим короткого замыкания (КЗ), ток I_кз называется ток короткого замыкания.

В обоих случаях мощность на нагрузке не выделяется.

В подавляющем большинстве случаев потребитель использует выходное напряжение U, поэтому, чтобы на внутреннем сопротивлении r не терялась мощность, желательно выполнение условия r «R, т. е. сопротивление нагрузки R должно быть велико.

Схему реального источника ЭДС можно заменить эквивалентной схемой источника тока, как показано на рисунке 1.13.

Источник тока J даёт ток, который не зависит от сопротивления нагрузки и всегда равен J. Рассмотрим, как преобразовать схему 1.12 в схему 1.13.
Как было показано раньше, E = U + Ir. Разделим обе части на r. Получим:

E/r = U/r + I.

В схеме на рис. 13: J = I₀ + I

Таким образом, схемы будут эквивалентны, если

J = E/r = I_кз
Чтобы уменьшить потери энергии на внутреннем сопротивлении r, нужно выполнение условия r»R.
^ Идеальный источник ЭДС обладает следующими свойствами:

1) Внутреннее сопротивление равно нулю: r = 0;

2) Напряжение на зажимах идеального источника ЭДС всегда равно Е и не зависит от сопротивления нагрузки R;

3) Ток через источник ЭДС определяется только сопротивлением нагрузки R: I = E/R;

4) Для идеального источника ЭДС невозможен режим короткого замыкания (т. к. при r = 0, I = ∞);

5) Идеальный источник ЭДС невозможно преобразовать в идеальный источник тока.

^ Идеальный источник тока
Свойства идеального источника тока:
1) Внутреннее сопротивление идеального источника тока бесконечно: r = ∞;

2) Ток через идеальный источник тока всегда равен J и не зависит от сопротивления нагрузки R;

3) Напряжение на нагрузке определяется только сопротивлением нагрузки R: U = JR;

4) Для идеального источника тока невозможен режим холостого хода (т. к. при r = ∞, U= Jr = ∞);

5) Идеальный источник тока невозможно преобразовать в идеальный источник ЭДС.
Идеальных источников тока и напряжения не существует, однако, во многих случаях, источник энергии можно считать идеальным. При r «R можно считать источник идеальным источником ЭДС, а при r» R – идеальным источником тока.
^ Соединение источников ЭДС
Несколько последовательно соединённых источников ЭДС можно заменить одним эквивалентным источником, как показано на рисунке 1.14.

Внутреннее сопротивление эквивалентного источника R_экв, как обычно при последовательном соединении, равно сумме внутренних сопротивлений всех источников.

R_экв = R₁ + R₂+ R₃

Напряжение эквивалентного источника ЭДС равно алгебраической сумме источников. При совпадении направлений – знак «+», в противном случае – знак «-». В данном случае:

Е_экв = Е₁ - Е₂ + Е₃

В случае идеальных источников ЭДС, очевидно, все сопротивления равны нулю и R_экв= 0.
Параллельное соединение идеальных источников ЭДС невозможно по определению. В случае реальных источников аналогично: несколько параллельно соединённых источников ЭДС можно заменить одним эквивалентным источником, как показано на рисунке 1.15.

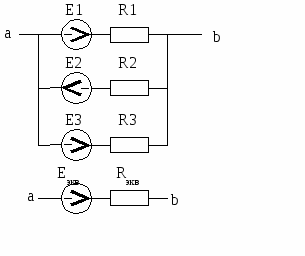
Рисунок 1.15 - Параллельное соединение нескольких источников ЭДС

Внутреннее сопротивление эквивалентного источника R_экв, определяется как обычно при параллельном соединении. Эквивалентная проводимость равна сумме проводимостей всех источников.

G_экв = = G₁+ G₂+ G₃, R_экв = 1/ G_экв

Эквивалентная ЭДС определяется по следующей формуле (в математике обычно используется термин «средневзвешенное значение»):

^ Соединение идеальных источников тока
Источники тока применяются достаточно редко, поэтому ограничимся рассмотрением только идеальных источников тока.

Последовательное соединение идеальных источников тока по определению невозможно.

При параллельном соединении несколько источников можно заменить одним эквивалентным, ток J которого равен алгебраической сумме токов источников.

УРОК №19

Date: 2016-05-25; view: 767; Нарушение авторских прав