Переходный процесс в цепи, содержащей катушку индуктивности

Рассмотрим теперь электрическую цепь, содержащую катушку индуктивности (рисунок 5).

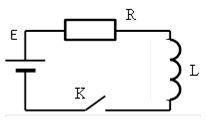
Пусть катушка обладает малым электрическим сопротивлением, меньшим, чем сопротивление резистора R. Внутренним сопротивлением источника тока пренебрежём. В момент времени t = 0 ключ К замыкается, и по цепи начинает протекать электрический ток. Если бы в цепи не было катушки индуктивности, то значение тока сразу бы установилось равным . Из-за явления самоиндукции нарастание тока в катушке будет постепенным. При этом в катушке возникает ЭДС самоиндукции 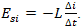. Здесь L — индуктивность катушки, 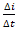— скорость изменения тока.

Так как резистор R и катушка L соединены последовательно, то E = U_R+ U_L.

Но U_R= iR, а U_L= - E_si. Тогда

(6)

При малых изменениях тока за малые промежутки времени () дробь 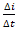превращается в производную силы тока как функции времени . Тогда уравнение (6) превращается в дифференциальное уравнение

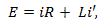
решение которого заключается в нахождении вида функции силы тока i(t) в катушке индуктивности от времени. Поступим так, как и в предыдущем случае. Представим уравнение (6) в виде

Время нарастания тока разобьём на малые одинаковые интервалы времени и посмотрим, как будет меняться его значение по истечении первого интервала от начала процесса, затем второго — и т.д. При этом, как уже было сказано,

Несложное преобразование даёт следующее

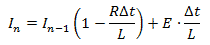
(7)

Выражение (7) также является рекуррентным и позволит определить изменение значения силы тока в катушке индуктивности через одинаковые промежутки времени. При известных величинах E, R и L. Самостоятельно выведите формулы (8)

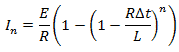
(8)

Можно также показать что при 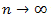установившееся значение силы тока в цепи

Обратим внимание, что в выражении (7) дробь безразмерна (докажите это).

Для определения количества интервалов времени n, а также самого интервала можно воспользоваться результатами предыдущего анализа. Время, за которое сила тока практически установится при точности амперметра, соответствующей

Пусть, например, E = 18В, R = 60Ом, L = 80Гн. Тогда T = 6,1с и при N = 100 имеем 0,061с. Эти данные соответствуют условию задания, приведённого в начале этой работы. Построим график, используя табличный процессор MS Excel (рисунке 6).

Красные маркеры поставлены в соответствии с таблицей к заданию, приведенному в начале работы. Как видно, теоретические расчёты хорошо согласуются с результатами измерений.

Придумаем задачу с переходным процессом!

Пусть конденсатор уже заряжен (рисунок 7). В некоторый момент времени t = 0 ключ К замыкается, и конденсатор начинает разряжаться через резистор R. Составьте задание для участников экзамена, где приведён ряд значений силы тока (или напряжения) в последовательные моменты времени. В условии может быть задано, например, начальное значение напряжения на конденсаторе (начальное значение силы разрядного тока), а также сопротивление резистора и ёмкость конденсатора.

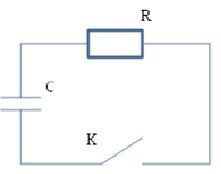
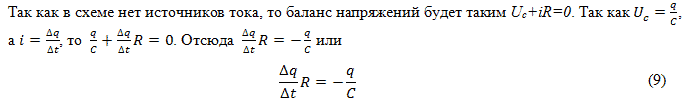
Из уравнения (9) видно, что скорость разряда конденсатора уменьшается по мере уменьшения остаточного заряда на конденсаторе. Весь процесс разряда также разобьём на одинаковые интервалы времени 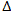t. Проделайте рассуждения самостоятельно и получите рекуррентную формулу

От рекуррентной формулы переходим к формуле для общего члена последовательности Un (выведите самостоятельно).

(10)

Здесь U₀ — начальное напряжение на конденсаторе.

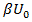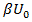Здесь напряжение уменьшается асимптотически до нуля. Будем считать, что конденсатор практически разрядится, если напряжение на нём будет составлять (например, ). Пусть значение U_n= достижимо за n = N шагов. Тогда

Если n = N соответствует длительности T процесса «практически полного» разряда конденсатора, то, учитывая 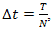, получим

(11)

Формулы (11) и (5) идентичны, так как соответствует .

Пусть конденсатор заряжен до напряжения U₀= 5В, RC = 0,001с. И, если N = 100, то T = 4,6 ^. RC и 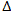t = 0,000046c Используя табличный процессор MS Excel, рассчитаем по формуле (10) значения U_n и построим график (рисунке 8).

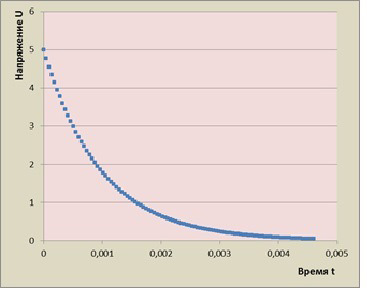
Из таблицы возьмём только 7-10 последовательных моментов времени из 100, относительно равномерно распределенных по всему графику.

УРОК №21

Графическое изображение изменения
напряжения в переходном процессе, постоянная времени.

График для приведен ниже.

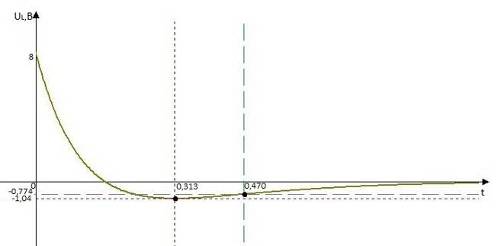
Рисунок 2.13 График переходного процесса напряжения на катушке.

Определим и построим (качественно) график переходного процесса для тока через индуктивность:

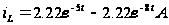
Начальные и конечные значения известны: , .

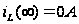Найдем экстремальное значение :

.

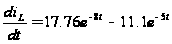При 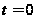производная (имеет положительное значение), т.е. кривая i(t) при 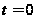от значения пойдет вверх.

Приравняем производную 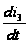нулю и найдем максимальное значение функции:

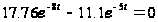
Максимум тока 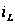функция принимает при .

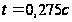Определим вторую производную и приравняв ее к нулю найдем точку перегиба тока :

,

,

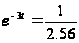
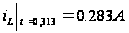
Максимум напряжения совпал с точкой перегиба криво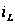й при .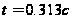

График для приведен ниже.

Рисунок 2.14 График переходного процесса тока на индуктивности.

Date: 2016-05-25; view: 807; Нарушение авторских прав