Интегральное исчисление

31. Понятие первообразной функции. Теорема о совокупности первообразных. Неопределенный интеграл, его свойства.

32. Метод замены переменной в неопределенном интеграле.

33. Метод интегрирования по частям. Основные типы интегралов, вычисляемых по частям.

34. Интегрирование рациональных дробей и рациональных тригонометрических функций.

35. Определенный интеграл как предел последовательности интегральных сумм. Свойства определенного интеграла, теорема о среднем.

36. Теорема о производной интеграла по переменному верхнему пределу. Формула Ньютона – Лейбница.

37. Методы замены переменной и интегрирования по частям в случае определенного интеграла.

38. Вычисление площади плоской фигуры и длины дуги кривой с помощью определенного интеграла.

39. Несобственные интегралы первого и второго рода, признаки сходимости.

40. Понятие двойного интеграла, его геометрический смысл, условия существования. Свойства двойного интеграла.

41. Метод вычисления двойного интеграла сведением его к интегралу повторному. Полярные координаты. Замена переменных в двойном интеграле.

42. Вычисление площадей плоской фигуры и поверхности с помощью двойного интеграла.

Дифференциальное исчисление функций одной переменной

Понятие функции

Рассмотрим множество элементов 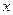и множество элементов .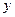

Определение. Если каждому элементу 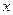ставится в соответствие по некоторому закону единственный элемент 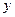, то говорят, что на множестве задана функция со значениями в множестве .

Элементы 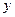- значения функции, элементы 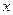- значения аргумента. Множество – область определения функции, - множество значений функции. Если и – множества действительных чисел, то функцию называют действительной функцией одного аргумента.

- закон, по которому устанавливается соответствие элементов, чаще всего, задается аналитически, то есть с помощью формулы. Аналитически функция может быть задана:

- явно: когда формула разрешена относительно 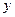. Например, .

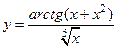- неявно: когда формула не разрешена относительно 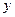. Например, .

- параметрически: когда 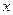и 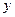заданы в виде явных функций

параметра : . Например, .

Определение. Графиком функции 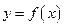называется множество точек плоскости с координатами .

Рассмотрим функцию с областью определения и множеством значений ₁ и функцию с областью определения ₂ иобластью значений .

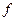Определение. Если область определения ₂ функции включает в себя множество значений ₁ функции , то говорят, что на множестве определена сложная функция c областью значений .

Например, 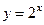, ₁= и , ₂=(). Таким образом, - сложная функция.

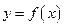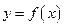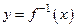Определение. Пусть - функция, имеющая областью определения множество D и областью значений множество Е, такова, что из условия следует , тогда каждому соответствует единственное значение , такое, что . Тем самым определена новая функция с областью определения Е и областью значений D. и называют взаимно обратными функциями.

Например, и .

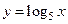Определение. Функция 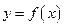называется четной, если удовлетворяет условию и нечетной, если .

Определение. Функция 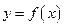называется периодической, если существует положительное число (период функции) такое, что для любого .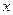

Определение. Функция 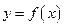называется строго возрастающей (убывающей) при , если для любых выполняется (). Строго возрастающая и строго убывающая функции называются строго монотонными.

Определение. Окрестностью точки называется любой открытый промежуток, содержащий эту точку. (эпсилон)- окрестностью точки называется промежуток 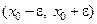длины с центром в точке .

Предел функции

Пусть переменная 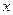стремится к (), то есть принимает значения сколь угодно близкие к , но не равные ему.

Определение. Число А называют пределом функции 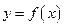в точке (при ), если для любого сколь угодно малого существует такое положительное число , что для всех 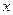, удовлетворяющих неравенству , выполняется неравенство . При этом пишут

.

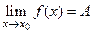Если 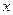неограниченно возрастает, то говорят, что 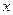стремится к плюс бесконечности: ; если неограниченно убывает, то .

Определение. Число А называют пределом функции 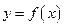при (), если для любого сколь угодно малого существует такое положительное число M, что для всех 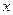, удовлетворяющих неравенству () выполняется неравенство . При этом пишут

.

Определение. Число А называют правым односторонним пределом функции 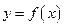при , если для любого сколь угодно малого существует такое положительное число , что для всех 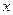, удовлетворяющих неравенству , выполняется неравенство . Пишут

.

Аналогично определяется левый односторонний предел функции в точке.

Свойства пределов

1. Если в окрестности точки : , то .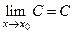

2. Если существуют конечные пределы функци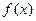й и в точке , то существуют пределы суммы, разности, произведения и частного этих функций (если ), причём

· ,

·

· ,

· .

3. Пусть существует предел 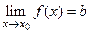и предел 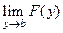. Пусть в некоторой окрестности точки 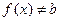, за исключением, быть может, самой точки , тогда существует предел сложной функции

Date: 2016-05-24; view: 369; Нарушение авторских прав