
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Квантовая природа излучения
|
|
Контрольная работа №3
«Оптика», «Атомная и ядерная физика»
| Вариант | Номера задач | ||||||||||||||||
| 1.1 | 1.14 | 1.18 | 2.10 | 2.14 | 2.32 | 3.9 | 3.11 | 4.10 | 4.34 | 4.52 | 5.1 | 5.23 | 5.31 | 6.1 | 6.47 | 6.70 | |
| 1.2 | 1.13 | 1.17 | 2.9 | 2.19 | 2.33 | 3.8 | 3.26 | 4.9 | 4.33 | 4.62 | 5.2 | 5.13 | 5.24 | 6.3 | 6.12 | 6.28 | |
| 1.3 | 1.12 | 1.20 | 2.8 | 2.17 | 2.30 | 3.7 | 3.19 | 4.8 | 4.31 | 4.54 | 5.3 | 5.14 | 5.22 | 6.5 | 6.20 | 6.35 | |
| 1.4 | 1.9 | 1.20 | 2.7 | 2.19 | 2.34 | 3.6 | 3.20 | 4.7 | 4.27 | 4.47 | 5.4 | 5.18 | 5.36 | 6.7 | 6.17 | 6.27 | |
| 1.5 | 1.16 | 1.21 | 2.6 | 2.22 | 2.40 | 3.14 | 3.22 | 4.6 | 4.22 | 4.38 | 5.5 | 5.19 | 5.27 | 6.9 | 6.13 | 6.32 | |
| 1.6 | 1.11 | 1.22 | 2.5 | 2.19 | 2.38 | 3.5 | 3.20 | 4.5 | 4.29 | 4.47 | 5.6 | 5.22 | 5.28 | 6.2 | 6.16 | 6.30 | |
| 1.7 | 1.15 | 1.19 | 2.4 | 2.15 | 2.29 | 3.7 | 3.15 | 4.4 | 4.18 | 4.46 | 5.7 | 5.19 | 5.34 | 6.4 | 6.18 | 6.36 | |
| 1.8 | 1.10 | 1.17 | 2.3 | 2.14 | 2.22 | 3.19 | 3.27 | 4.3 | 4.44 | 4.62 | 5.8 | 5.18 | 5.26 | 6.6 | 6.22 | 6.28 | |
| 1.9 | 1.19 | 1.22 | 2.2 | 2.13 | 2.24 | 3.11 | 3.18 | 4.2 | 4.13 | 4.34 | 5.9 | 5.13 | 5.32 | 6.8 | 6.48 | 6.76 | |
| 1.10 | 1.14 | 1.19 | 2.1 | 2.17 | 2.39 | 3.2 | 3.16 | 4.1 | 4.33 | 4.61 | 5.1 | 5.14 | 5.29 | 6.1 | 6.23 | 6.31 | |
| 1.11 | 1.16 | 1.20 | 2.1 | 2.14 | 2.29 | 3.9 | 3.13 | 4.5 | 4.20 | 4.45 | 5.2 | 5.21 | 5.34 | 6.3 | 6.44 | 6.72 | |
| 1.12 | 1.20 | 1.21 | 2.2 | 2.21 | 2.38 | 3.12 | 3.20 | 4.6 | 4.30 | 4.61 | 5.3 | 5.12 | 5.28 | 6.5 | 6.36 | 6.75 | |
| 1.1 | 1.21 | 1.23 | 2.3 | 2.12 | 2.28 | 3.6 | 3.22 | 4.7 | 4.29 | 4.54 | 5.4 | 5.20 | 5.35 | 6.7 | 6.49 | 6.64 | |
| 1.2 | 1.17 | 1.21 | 2.4 | 2.18 | 2.36 | 3.3 | 3.15 | 4.8 | 4.38 | 4.56 | 5.5 | 5.16 | 5.25 | 6.9 | 6.19 | 6.33 | |
| 1.3 | 1.12 | 1.20 | 2.5 | 2.16 | 2.25 | 3.4 | 3.29 | 4.9 | 4.29 | 4.53 | 5.6 | 5.20 | 5.31 | 6.2 | 6.43 | 6.74 | |
| 1.4 | 1.18 | 1.22 | 2.6 | 2.20 | 2.31 | 3.2 | 3.24 | 4.10 | 4.21 | 4.43 | 5.7 | 5.17 | 5.27 | 6.4 | 6.45 | 6.79 | |
| 1.5 | 1.20 | 1.23 | 2.7 | 2.15 | 2.37 | 3.9 | 3.19 | 4.1 | 4.47 | 4.60 | 5.8 | 5.21 | 5.34 | 6.6 | 6.50 | 6.71 | |
| 1.6 | 1.22 | 1.23 | 2.8 | 2.18 | 2.39 | 3.3 | 3.12 | 4.2 | 4.31 | 4.54 | 5.9 | 5.18 | 5.36 | 6.8 | 6.21 | 6.34 | |
| 1.7 | 1.17 | 1.21 | 2.9 | 2.11 | 2.18 | 3.2 | 3.21 | 4.3 | 4.32 | 4.58 | 5.1 | 5.19 | 5.33 | 6.1 | 6.14 | 6.29 | |
| 1.8 | 1.16 | 1.20 | 2.10 | 2.21 | 2.40 | 3.8 | 3.17 | 4.4 | 4.36 | 4.55 | 5.2 | 5.15 | 5.37 | 6.3 | 6.17 | 6.30 |
Литература
1. Волькенштейн В.С. Сборник задач по курсу физики. – СПб.: СпецЛит, 2001.
2. Трофимова Т.И. Сборник задач по курсу физики для втузов. – М.: «Оникс 21 век», «Мир и Образование», 2003.
Интерференция света
1.1. Определить длину отрезка l 1, на котором укладывается столько же длин волн монохроматического света в вакууме, сколько их укладывается на отрезке l 2 = 5 мм в стекле. Показатель преломления стекла n 2 = 1,5.
1.2. В опыте с зеркалами Френеля расстояние d между мнимыми изображениями источника света равно 0,5 мм, расстояние l от них до экрана равно 5 м. В желтом свете ширина интерференционных полос равна 6 мм. Определить длину волны желтого света.
1.3. Расстояние между двумя щелями в опыте Юнга d = 0,5 мм (λ=0,6 мкм). Определить расстояние l от щелей до экрана, если ширина Δx интерференционных полос равна 1,2 мм.
1.4. В опыте Юнга расстояние l от щелей до экрана равно 3 м. Определить угловое расстояние между соседними светлыми полосами, если третья светлая полоса на экране отстоит от центра интерференционной картины на расстоянии 4,5 мм.
1.5. Если в опыте Юнга на пути одного из интерферирующих лучей поместить перпендикулярно этому лучу тонкую стеклянную пластинку (п = 1,5), то центральная светлая полоса смещается в положение, первоначально занимаемое пятой светлой полосой. Длина волны λ = 0,5 мкм. Определить толщину пластинки.
1.6. Определить, во сколько раз изменится ширина интерференционных полос на экране в опыте с зеркалами Френеля, если фиолетовый светофильтр (0,4 мкм) заменить красным (0,7 мкм).
1.7. Расстояние от бипризмы Френеля до узкой щели и экрана соответственно равны а = 30 см и b = 1,5 м. Бипризма стеклянная (n = 1,5) с преломляющим углом Θ = 20'. Определить длину волны света, если ширина интерференционных полос Δ x = 0,65 мм.
1.8. Расстояния от бипризмы Френеля до узкой щели и экрана соответственно равны a = 48 см и b = 6 м. Бипризма стеклянная (n = 1,5) с преломляющим углом Θ = 10'. Определить максимальное число полос, наблюдаемых на экране, если λ = 600 нм.
1.9. На плоскопараллельную пленку с показателем преломления n = 1,33 под углом α = 45° падает параллельный пучок белого света. Определить, при какой наименьшей толщине пленки зеркально отраженный свет наиболее сильно окрасится в желтый свет (λ = 0,6 мкм).
1.10. На стеклянный клин (n = 1,5) нормально падает монохроматический свет (λ = 698 нм). Определить угол между поверхностями клина, если расстояние между двумя соседними интерференционными минимумами в отраженном свете равно 2 мм.
1.11. На стеклянный клин (n = 1,5) нормально падает монохроматический свет. Угол клина равен 4'. Определить длину световой волны, если расстояние между двумя соседними интерференционными максимумами в отраженном свете равно 0,2 мм.
1.12. На тонкую мыльную пленку (n = 1,33) под углом Θ = 30° падает монохроматический свет с длиной волны λ = 0,6 мкм. Определить угол между поверхностями пленки, если расстояние b между интерференционными полосами в отраженном свете равно 4 мм.
1.13. Монохроматический свет падает нормально на поверхность воздушного клина, причем расстояние между интерференционными полосами Δ x 1 = 0,4 мм. Определить расстояние Δ x 2 между интерференционными полосами, если пространство между пластинками, образующими клин, заполнить прозрачной жидкостью с показателем преломления n = 1,33.
1.14. Плосковыпуклая линза радиусом кривизны 4 м выпуклой стороной лежит на стеклянной пластинке. Определить длину волны падающего монохроматического света, если радиус пятого светлого кольца в отраженном свете равен 3 мм.
1.15. Установка для наблюдения колец Ньютона освещается монохроматическим светом с длиной волны λ = 0,6 мкм, падающим нормально. Пространство между линзой и стеклянной пластинкой заполнено жидкостью, и наблюдение ведется в проходящем свете. Радиус кривизны линзы R = 4 м. Определить показатель преломления жидкости, если радиус второго светлого кольца r = 1,8 мм.
1.16. Установка для наблюдения колец Ньютона освещается монохроматическим светом с длиной волны λ = 0,55 мкм, падающим нормально. Определить толщину воздушного зазора, образованного плоскопараллельной пластинкой и соприкасающейся с ней плосковыпуклой линзой в том месте, где в отраженном свете наблюдается четвертое темное кольцо.
1.17. Плосковыпуклая линза с показателем преломления n = 1,6 выпуклой стороной лежит на стеклянной пластинке. Радиус третьего светлого кольца в отраженном свете (λ = 0,6 мкм) равен 0,9 мм. Определить фокусное расстояние линзы.
1.18. Плосковыпуклая линза с радиусом сферической поверхности R = 12,5 см прижата к стеклянной пластинке. Диаметры десятого и пятнадцатого темных колец Ньютона в отраженном свете соответственно равны 1 и 1,5 мм. Определить длину волны света.
1.19. Установка для наблюдения колец Ньютона освещается монохроматическим светом, падающим нормально. При заполнении пространства между линзой и стеклянной пластинкой прозрачной жидкостью радиусы темных колец в отраженном свете уменьшились в 1,21 раза. Определить показатель преломления жидкости.
1.20. Для уменьшения потерь света из-за отражения от поверхностей стекла осуществляют «просветление оптики»: на свободные поверхности линз наносят тонкие пленки с показателем преломления 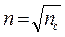 . В этом случае амплитуды отраженных лучей от обеих поверхностей такой пленки одинаковы. Определить толщину слоя, при которой отражение для света с длиной волны λ от стекла в направлении нормали равна нулю.
. В этом случае амплитуды отраженных лучей от обеих поверхностей такой пленки одинаковы. Определить толщину слоя, при которой отражение для света с длиной волны λ от стекла в направлении нормали равна нулю.
1.21. Определить длину волны света в опыте с интерферометром Майкельсона, если для смещения интерференционной картины на 112 полос зеркало пришлось переместить на расстояние l = 33 мкм.
1.22. Для измерения показателя преломления аммиака в одно из плеч интерферометра Майкельсона помещена закрытая с обеих сторон откачанная до высокого вакуума стеклянная трубка длиной l = 15 см. При заполнении трубки аммиаком интерференционная картина для длины волны λ= 589 нм сместилась на 192 полосы. Определить показатель преломления аммиака.
1.23. На пути лучей интерференционного рефрактометра помещаются трубки длиной l = 2 см с плоскопараллельными стеклянными основаниями, наполненные воздухом (n0 = 1,000277). Одну трубку заполнили хлором, и при этом интерференционная картина сместилась на m0 = 20 полос. Определить показатель преломления хлора, если наблюдения производятся с монохроматическим светом с длиной волны λ = 589 нм.
Дифракция света
2.1. Точечный источник света (λ = 0,5 мкм) расположен на расстоянии а = 1 м перед диафрагмой с круглым отверстием диаметра d = 2 мм. Определить расстояние b от диафрагмы до точки наблюдения, если отверстие открывает три зоны Френеля.
2.2. Определить радиус третьей зоны Френеля, если расстояния от точечного источника света (λ = 0,6 мкм) до волновой поверхности и от волновой поверхности до точки наблюдения равны 1,5 м.
2.3. На диафрагму с круглым отверстием диаметром d = 5 мм падает нормально параллельный пучок света с длиной волны λ = 0,6 мкм. Определить расстояние от точки наблюдения до отверстия, если отверстие открывает: 1) две зоны Френеля; 2) три зоны Френеля.
2.4. Определить радиус третьей зоны Френеля для случая плоской волны. Расстояние от волновой поверхности до точки наблюдения равно 1,5 м. Длина волны λ = 0,6 мкм.
2.5. Определить радиус четвертой зоны Френеля, если радиус второй зоны Френеля для плоского волнового фронта равен 2 мм.
2.6. Определить радиус первой зоны Френеля, если расстояния от точечного источника света (λ = 0,5 мкм) до зонной пластинки и от пластинки до места наблюдения а = b = 1 м.
2.7. На зонную пластинку падает плоская монохроматическая волна (λ = 0,5 мкм). Определить радиус первой зоны Френеля, если расстояние от зонной пластинки до места наблюдения b = 1 м.
2.8. Зонная пластинка дает изображение источника, удаленного от нее на 2 м, на расстоянии 1 м от своей поверхности. Где получится изображение источника, если его удалить в бесконечность?
2.9. Дифракция наблюдается на расстоянии 1 м от точечного источника монохроматического света (λ = 0,5 мкм). Посередине между источником света и экраном находится диафрагма с круглым отверстием. Определить радиус отверстия, при котором центр дифракционных колец на экране является наиболее темным.
2.10. Сферическая волна, распространяющаяся из точечного монохроматического источника света (λ = 0,6 мкм), встречает на своем пути экран с круглым отверстием радиусом r = 0,4 мм. Расстояние b от источника до экрана равно 1 м. Определить расстояние от отверстия до точки экрана, лежащей на линии, соединяющей источник с центром отверстия, где наблюдается максимум освещенности.
2.11. На экран с круглым отверстием радиусом r = 1,5 мм нормально падает параллельный пучок монохроматического света с длиной волны λ = 0,5 мкм. Точка наблюдения находится на оси отверстия на расстоянии b = 1,5 м от него. Определить: 1) число зон Френеля, укладывающихся в отверстии; 2) темное или светлое кольцо наблюдается в центре дифракционной картины, если в месте наблюдения помещен экран.
2.12. На экран с круглым отверстием радиусом r = 1,2 мм нормально падает параллельный пучок монохроматического света с длиной волны λ = 0,6 мкм. Определить максимальное расстояние от отверстия на его оси, где еще можно наблюдать наиболее темное пятно.
2.13. Показать, что за круглым экраном С в точке В, лежащей на линии, соединяющей точечный источник с центром экрана, будет наблюдаться светлое пятно. Размеры экрана принять достаточно малыми.
2.14. На узкую щель шириной b = 0,05 мм падает нормально монохроматический свет с длиной волны λ = 694 нм. Определить направление света на вторую светлую дифракционную полосу (по отношению к первоначальному направлению света).
2.15. На узкую щель падает нормально монохроматический свет. Его направление на четвертую темную дифракционную полосу составляет 2°12'. Определить, сколько длин волн укладывается на ширине щели.
2.16. На щель шириной а = 0,1 мм падает нормально монохроматический свет (λ = 0,6 мкм). Экран, на котором наблюдается дифракционная картина, расположен параллельно щели на расстоянии l = 1 м. Определить расстояние Δxмежду первыми дифракционными минимумами, расположенными по обе стороны центрального фраунгоферова максимума.
2.17. На щель шириной а = 0,1 мм падает нормально монохроматический свет с длиной волны λ = 0,5 мкм. Дифракционная картина наблюдается на экране, расположенном параллельно щели. Определить расстояние l от щели до экрана, если ширина центрального дифракционного максимума Δx = 1 см.
2.18. Монохроматический свет с длиной волны λ = 0,6 мкм падает на длинную прямоугольную щель шириной а = 12 мкм под углом Θ = 45° к ее нормали. Определить угловое положение первых минимумов, расположенных по обе стороны центрального фраунгоферова максимума.
2.19. Монохроматический свет падает на длинную прямоугольную щель шириной а = 12 мкм под углом α = 30° к ее нормали. Определить длину волны λ света, если направление на первый минимум (k = 1) от центрального фраунгоферова максимума составляет 33°.
2.20. На дифракционную решетку нормально падает монохроматический свет с длиной волны λ = 600 нм. Определить наибольший порядок спектра, полученный с помощью этой решетки, если ее постоянная d = 2 мкм.
2.21. На дифракционную решетку длиной l = 1,5 мм, содержащей N = 3000 штрихов, падает нормально монохроматический свет с длиной волны λ = 550 нм. Определить: 1) число максимумов, наблюдаемых в спектре дифракционной решетки; 2) угол, соответствующий последнему максимуму.
2.22. Определить число штрихов на 1 мм дифракционной решетки, если углу φ= 30° соответствует максимум четвертого порядка для монохроматического света с длиной волны λ= 0,5 мкм.
2.23. На дифракционную решетку нормально падает монохроматический свет с длиной волны λ = 0,5 мкм. На экран, находящийся от решетки на расстоянии L = 1 м, с помощью линзы, расположенной вблизи решетки, проецируется дифракционная картина, причем первый главный максимум наблюдается на расстоянии l = 15 см от центрального. Определить число штрихов на 1 см дифракционной решетки.
2.24. Монохроматический свет нормально падает на дифракционную решетку. Определить угол дифракции, соответствующий максимуму четвертого порядка, если максимум третьего порядка отклонен на φ = 18°.
2.25. На дифракционную решетку нормально падает монохроматический свет. Определить угол дифракции для линии 0,55 мкм в четвертом порядке, если этот угол для линии 0,6 мкм в третьем порядке составляет 30°.
2.26. На дифракционную решетку нормально падает монохроматический свет. В спектре, полученном с помощью этой дифракционной решетки, некоторая спектральная линия наблюдается в первом порядке под углом φ = 11°. Определить наивысший порядок спектра, в котором может наблюдаться эта линия.
2.27. Определить длину волны монохроматического света, падающего нормально на дифракционную решетку, имеющую 300 штрихов на 1 мм, если угол между направлениями на максимумы первого и второго порядков составляет 12°.
2.28. Определить толщину плоскопараллельной стеклянной пластинки (п = 1,55), при которой в отраженном свете максимум второго порядка для λ = 0,65 мкм наблюдается под тем же углом, что и у дифракционной решетки с постоянной d = 1 мкм.
2.29. На дифракционную решетку с постоянной d = 5 мкм под углом Θ = 30° падает монохроматический свет с длиной волны λ = 0,5 мкм. Определить угол φ дифракции для главного максимума третьего порядка.
2.30. На дифракционную решетку под углом Θ падает монохроматический свет с длиной волны λ. Найти условие, определяющее направления на главные максимумы, при условии, что d >> m λ (m – порядок спектра).
2.31. Узкий параллельный пучок рентгеновского излучения с длиной волны λ = 245 нм падает на естественную грань монокристалла каменной соли. Определить расстояние d между атомными плоскостями монокристалла, если дифракционный максимум второго порядка наблюдается при падении излучения к поверхности монокристалла под углом скольжения Θ = 61°.
2.32. Узкий параллельный пучок монохроматического рентгеновского излучения падает на грань кристалла с расстоянием d между его атомными плоскостями 0,3 нм. Определить длину волны рентгеновского излучения, если под углом Θ = 30° к плоскости грани наблюдается дифракционный максимум первого порядка.
2.33. На дифракционную решетку нормально падает монохроматический свет с длиной волны λ = 0,6 мкм. Угол дифракции для пятого максимума равен 30°, а минимальная разрешаемая решеткой разность длин волн составляет Δλ = 0,2 нм. Определить: 1) постоянную дифракционной решетки; 2) длину дифракционной решетки.
2.34. Сравнить наибольшую разрешающую способность для красной линии кадмия (λ= 644 нм) двух дифракционных решеток одинаковой длины (l = 5 мм), но разных периодов (d1 = 4 мкм, d2 = 8 мкм).
2.35. Показать, что для данной λ максимальная разрешающая способность дифракционных решеток, имеющих разные периоды, но одинаковую длину, имеет одно и то же значение.
2.36. Определить постоянную дифракционной решетки, если она в первом порядке разрешает две спектральные линии калия (λ1 = 578 нм и λ2 = 580 нм). Длина решетки l = 1 см.
2.37. Постоянная d дифракционной решетки длиной l = 2,5 см равна 5 мкм. Определить разность длин волн, разрешаемую этой решеткой, для света с длиной волны λ = 0,5 мкм в спектре второго порядка.
2.38. Дифракционная решетка имеет N = 1000 штрихов и постоянную d = 10 мкм. Определить: 1) угловую дисперсию для угла дифракции φ = 30° в спектре третьего порядка; 2) разрешающую способность дифракционной решетки в спектре пятого порядка.
2.39. Определить длину волны, для которой дифракционная решетка с постоянной d = 3 мкм в спектре второго порядка имеет угловую дисперсию D = 7.105 рад/м.
2.40. Угловая дисперсия дифракционной решетки для λ = 500 нм в спектре второго порядка равна 4,08.105 рад/м. Определить постоянную дифракционной решетки.
Поляризация света
3.1. Описать поведение светового вектора Е в данной точке пространства в случае эллиптически поляризованного света.
3.2. Определить степень поляризации частично поляризованного света, если амплитуда светового вектора, соответствующая максимальной интенсивности света, в 3 раза больше амплитуды, соответствующей его минимальной интенсивности.
3.3. Степень поляризации частично поляризованного света составляет 0,75. Определить отношение максимальной интенсивности света, пропускаемого анализатором, к минимальной.
3.4. Определить степень поляризации P света, который представляет собой смесь естественного света с плоскополяризованным, если интенсивность поляризованного света равна интенсивности естественного.
3.5. Определить степень поляризации P света, который представляет собой смесь естественного света с плоскополяризованным, если интенсивность поляризованного света в 5 раз больше интенсивности естественного.
3.6. Угол между главными плоскостями поляризатора и анализатора составляет 30°. Определить изменение интенсивности прошедшего через них света, если угол между главными плоскостями равен 45°.
3.7. Интенсивность естественного света, прошедшего через два николя, уменьшилась в 8 раз. Пренебрегая поглощением света, определить угол между главными плоскостями николей.
3.8. Определить, во сколько раз ослабится интенсивность света, прошедшего через два николя, расположенные так, что угол между их главными плоскостями α = 60°, а в каждом из николей теряется 8 % интенсивности падающего на него света.
3.9. Определить, во сколько раз уменьшится интенсивность естественного света, прошедшего через два николя, главные плоскости которых образуют угол в 60°, если каждый из николей как поглощает, так и отражает 5 % падающего на них света.
3.10. Естественный свет проходит через поляризатор и анализатор, угол между главными плоскостями которых равен α. Поляризатор и анализатор как поглощают, так и отражают 10 % падающего на них света. Определить угол α, если интенсивность света, вышедшего из анализатора, равна 12 % интенсивности света, падающего на поляризатор.
3.11. Естественный свет интенсивностью I0 проходит через поляризатор и анализатор, угол между главными плоскостями которых составляет α. После прохождения света через эту систему он падает на зеркало и, отразившись, проходит вновь через нее. Пренебрегая поглощением света, определить интенсивность I света после его обратного прохождения.
3.12. Доказать, что при падении света на границу раздела двух сред под углом Брюстера отраженный и преломленный лучи взаимно перпендикулярны.
3.13. Пучок естественного света падает под углом α = 30° к стеклянной поверхности. Определить показатель преломления стекла, если отраженный луч является плоскополяризованным.
3.14. Определить показатель преломления стекла, если при отражении от него света отраженный луч полностью поляризован при угле преломления 35°.
3.15. Определить, под каким углом к горизонту должно находиться Солнце, чтобы лучи, отраженные от поверхности озера (n = 1,33), были максимально поляризованы.
3.16. Свет, проходя через жидкость, налитую в стеклянный сосуд (n = 1,5), отражается от дна, причем отраженный свет плоскополяризован при падении его на дно сосуда под углом 41°. Определить: 1) показатель преломления жидкости; 2) угол падения света на дно сосуда, чтобы наблюдалось полное отражение.
3.17. Параллельный пучок света падает нормально на пластинку из исландского шпата, толщиной 50 мкм, вырезанную параллельно оптической оси. Принимая показатели преломления исландского шпата для обыкновенного и необыкновенного лучей соответственно n0 = 1,66 и nе = 1,49, определить разность хода этих лучей, прошедших через пластинку.
3.18. Плоскополяризованный свет, длина волны которого в вакууме λ = 589 нм, падает на пластинку исландского шпата перпендикулярно его оптической оси. Принимая показатели преломления исландского шпата для обыкновенного и необыкновенного лучей соответственно п0 = 1,66 и пе= 1,49, определить длины волн этих лучей в кристалле.
3.19. Плоскополяризованный свет, длина волны которого в вакууме λ = 530 нм, падает на пластинку из кварца перпендикулярно его оптической оси. Определить показатели преломления кварца для обыкновенного (n0) и необыкновенного (nе) лучей, если длины волн этих лучей в кристалле соответственно равны λ0 = 344 нм и λe = 341 нм.
3.20. Определить наименьшую толщину кристаллической пластинки в четверть волны для n = 530 нм, если разность показателей преломления обыкновенного и необыкновенного лучей для данной длины волны пе – n0 = 0,01. Пластинкой в четверть волны называется кристаллическая пластинка, вырезанная параллельно оптической оси, при прохождении через которую в направлении, перпендикулярном оптической оси, обыкновенный и необыкновенный лучи, не изменяя своего направления, приобретают разность хода, равную λ/4.
3.21. Используя задачу 4.20, дать определение кристаллической пластинки «в целую волну» и определить ее наименьшую толщину для λ = 530 нм, если разность показателей преломления обыкновенного и необыкновенного лучей для данной длины волны п0 – ne = 0,01.
3.22. Объяснить, изменится ли наблюдаемая оптическая картина в случае эффекта Керра, если направление электрического поля изменить на противоположное.
3.23. Определить толщину кварцевой пластинки, для которой угол поворота плоскости поляризации монохроматического света определенной длины волны φ = 180°. Удельное вращение в кварце для данной длины волны α = 0,52 рад/мм.
3.24. Пластинка кварца толщиной d1 = 2 мм, вырезанная перпендикулярно оптической оси кристалла, поворачивает плоскость поляризации монохроматического света определенной длины волны на угол φ1 = 30°. Определить толщину d2 кварцевой пластинки, помещенной между параллельными николями, чтобы данный монохроматический свет гасился полностью.
3.25. Определить массовую концентрацию С сахарного раствора, если при прохождении света через трубку длиной l = 20 см с этим раствором плоскость поляризации света поворачивается на угол φ = 10°. Удельное вращение α сахара равно 1,17.10-2 рад.м2/кг.
3.26. Раствор глюкозы с массовой концентрацией C1 = 0,21 г/см3, находящийся в стеклянной трубке, поворачивает плоскость поляризации монохроматического света, проходящего через раствор, на угол φ1 = 24°. Определить массовую концентрацию С2 глюкозы в другом растворе в трубке такой же длины, если он поворачивает плоскость поляризации на угол φ2 = 18°.
3.27. Плоскополяризованный монохроматический свет, прошедший через поляроид, оказывается полностью погашенным. Если же на пути света поместить кварцевую пластинку, то интенсивность прошедшего через поляроид света уменьшается в 3 раза (по сравнению с интенсивностью света, падающего на поляроид). Принимая удельное вращение в кварце α = 0,52 рад/мм и пренебрегая потерями света, определить минимальную толщину кварцевой пластинки.
Квантовая природа излучения
4.1. Объяснить, почему в неотапливаемом помещении температура всех тел одинакова.
4.2. Объяснить, почему открытые окна домов со стороны улиц кажутся черными.
4.3. Чайная фарфоровая чашка на светлом фоне имеет темный рисунок. Объяснить, почему если эту чашку быстро вынуть из печи, где она нагревалась до высокой температуры, и рассматривать в темноте, то наблюдается светлый рисунок на темном фоне.
4.4. Имеется два одинаковых алюминиевых чайника, в которых до одной и той же температуры нагрето одинаковое количество воды. Один чайник закопчен, а другой – чистый. Объяснить, какой из чайников остынет быстрее и почему.
4.5. Определить, во сколько раз необходимо уменьшить термодинамическую температуру черного тела, чтобы его энергетическая светимость Rэ ослабилась в 16 раз.
4.6. Температура внутренней поверхности муфельной печи при открытом отверстии площадью 30 см2 равна 1,3 кК. Принимая, что отверстие печи излучает как черное тело, определить, какая часть мощности рассеивается стенками, если потребляемая печью мощность составляет 1,5 кВт.
4.7. Энергетическая светимость черного тела Rэ = 10 кВт/м2. Определить длину волны, соответствующую максимуму спектральной плотности энергетической светимости этого тела.
4.8. Определить, как и во сколько раз изменится мощность излучения черного тела, если длина волны, соответствующая максимуму его спектральной плотности энергетической светимости, сместилась с λ1 = 720 нм до λ2 = 400 нм.
4.9. Черное тело находится при температуре T1 = 3 кК. При остывании тела длина волны, соответствующая максимуму спектральной плотности энергетической светимости, изменилась на Δλ = 8 мкм. Определить температуру Т2, до которой тело охладилось.
4.10. Черное тело нагрели от температуры T1 = 600 К до Т2 = 2400 К. Определить: 1) во сколько раз увеличилась его энергетическая светимость; 2) как изменилась длина волны, соответствующая максимуму спектральной плотности энергетической светимости.
4.11. Площадь, ограниченная графиком спектральной плотности энергетической светимости rλT черного тела, при переходе от термодинамической температуры Т1 к температуре Т2 увеличилась в 5 раз. Определить, как изменится при этом длина волны λmax, соответствующая максимуму спектральной плотности энергетической светимости черного тела.
4.12. В результате нагревания черного тела длина волны, соответствующая максимуму спектральной плотности энергетической светимости, сместилась с λ1 = 2,7 мкм до λ2 = 0,9 мкм. Определить, во сколько раз увеличилась: 1) энергетическая светимость тела; 2) максимальная спектральная плотность энергетической светимости тела. Максимальная спектральная плотность энергетической светимости черного тела возрастает согласно закону rλT = СТ5,
где С = 1,3.10-5 Вт/(м3.К5).
4.13. Определить, какая длина волны соответствует максимальной спектральной плотности энергетической светимости (rλT)max, равной 1,3.1011 (Вт/м2)/м (см. задачу 5.12).
4.14. Считая никель черным телом, определить мощность, необходимую для поддержания температуры расплавленного никеля 1453 °С неизменной, если площадь его поверхности равна 0,5 см2. Потерями энергии пренебречь.
4.15. Металлическая поверхность площадью S = 15 см2, нагретая до температуры Т = 3000 К, излучает в одну минуту 100 кДж. Определить: 1) энергию, излучаемую этой поверхностью, считая ее черной; 2) отношение энергетических светимостей этой поверхности и черного тела при данной температуре.
4.16. Принимая Солнце за черное тело, и учитывая, что его максимальной спектральной плотности энергетической светимости соответствует длина волны λ = 500 нм, определить: 1) температуру поверхности Солнца; 2) энергию, излучаемую Солнцем в виде электромагнитных волн за 10 мин; 3) массу, теряемую Солнцем за это время за счет излучения.
4.17. Определить температуру тела, при которой оно при температуре окружающей среды t0 = 23 °С излучало энергии в 10 раз больше, чем поглощало.
4.18. Считая, что тепловые потери обусловлены только излучением, определить, какую мощность необходимо подводить к медному шарику диаметром d = 2 см, чтобы при температуре окружающей среды t0 = -13 °С поддерживать его температуру равной t = 17 °C. Принять поглощательную способность меди АT = 0,6.
4.19. Определить силу тока, протекающего по вольфрамовой проволоке диаметром d = 0,8 мм, температура которой в вакууме поддерживается постоянной и равной t = 2800 °С. Поверхность проволоки принять в качестве серой с поглощательной способностью АT = 0,343. Удельное сопротивление проволоки при данной температуре ρ = 0,92.10-4 Ом.см. Температура окружающей проволоку среды t0 = 17 °C.
4.20. Преобразовать формулу Планка для спектральной плотности энергетической светимости черного тела от переменной ν к переменной λ.
4.21. Используя формулу Планка, определить спектральную плотность потока излучения единицы поверхности черного тела, приходящегося на узкий интервал длин волн Δλ = 5 нм около максимума спектральной плотности энергетической светимости, если температура черного тела Т = 2500 К.
4.22. Объяснить: 1) происхождение радиационной, цветовой и яркостной температур; 2) может ли радиационная температура быть больше истинной.
4.23. Для вольфрамовой нити при температуре Т = 3500 К поглощательная способность АT = 0,35. Определить радиационную температуру нити.
4.24. Отношение энергетической светимости RCT серого тела к энергетической светимости RЭ черного тела равно AT. Вывести связь между истинной и радиационной температурами.
4.25. Определить максимальную скорость фотоэлектронов, вырываемых с поверхности металла, если фототок прекращается при приложении задерживающего напряжения U0 = 3,7 В.
4.26. «Красная граница» фотоэффекта для некоторого металла равна 500 нм. Определить минимальное значение энергии фотона, вызывающего фотоэффект.
4.27. Фотоэлектроны, вырываемые с поверхности металла, полностью задерживаются при приложении обратного напряжения U0 = 3 В. Фотоэффект для этого металла начинается при частоте падающего монохроматического света ν0 = 6.1014 с-1. Определить: 1) работу выхода электронов из этого металла; 2) частоту применяемого облучения.
4.28. Определить работу выхода А электронов из вольфрама, если «красная граница» фотоэффекта для него λ0 = 275 нм.
4.29. Калий освещается монохроматическим светом с длиной волны 400 нм. Определить наименьшее задерживающее напряжение, при котором фототок прекратится. Работа выхода электронов из калия равна 2,2 эВ.
4.30. «Красная граница» фотоэффекта для некоторого металла равна 500 нм. Определить: 1) работу выхода электронов из этого металла; 2) максимальную скорость электронов, вырываемых из этого металла светом с длиной волны 400 нм.
4.31. Выбиваемые светом при фотоэффекте электроны при облучении фотокатода видимым светом полностью задерживаются обратным напряжением U0 = l,2 B. Специальные измерения показали, что длина волны падающего света λ = 400 нм. Определить «красную границу» фотоэффекта.
4.32. Задерживающее напряжение для платиновой пластинки (работа выхода 6,3 эВ) составляет 3,7 В. При тех же условиях для другой пластинки задерживающее напряжение равно 5,3 В. Определить работу выхода электронов из этой пластинки.
4.33. Определить, до какого потенциала зарядится уединенный серебряный шарик при облучении его ультрафиолетовым светом длиной волны λ = 280 нм. Работа выхода электронов из серебра А = 4,7 эВ.
4.34. При освещении вакуумного фотоэлемента монохроматическим светом с длиной волны λ1 = 0,4 мкм он заряжается до разности потенциалов φ1 = 2 В. Определить, до какой разности потенциалов зарядится фотоэлемент при освещении его монохроматическим светом с длиной волны λ2 = 0,3 мкм.
4.35. Плоский серебряный электрод освещается монохроматическим излучением с длиной волны λ = 83 нм. Определить, на какое максимальное расстояние от поверхности электрода может удалиться фотоэлектрон, если вне электрода имеется задерживающее электрическое поле напряженностью Е = 10 В/см. «Красная граница» фотоэффекта для серебра λ0 = 264 нм.
4.36. Фотоны с энергией ε = 5 эВ вырывают фотоэлектроны из металла с работой выхода А = 4,7 эВ. Определить максимальный импульс, передаваемый поверхности этого металла при вылете электрона.
4.37. При освещении катода вакуумного фотоэлемента монохроматическим светом с длиной волны λ = 310 нм фототок прекращается при некотором задерживающем напряжении. При увеличении длины волны на 25 % задерживающее напряжение оказывается меньше на 0,8 В. Определить по этим экспериментальным данным постоянную Планка.
4.38. Определить максимальную скорость υmaxфотоэлектронов, вырываемых с поверхности цинка (работа выхода А = 4 эВ), при облучении γ-излучением с длиной волны λ = 2,47 пм.
4.39. Определить для фотона с длиной волны λ = 0,5 мкм: 1) его энергию; 2) импульс; 3) массу.
4.40. Определить энергию фотона, при которой его масса равна массе покоя электрона. Ответ выразить в электрон-вольтах.
4.41. Определить, с какой скоростью должен двигаться электрон, чтобы его импульс был равен импульсу фотона, длина волны которого λ = 0,5 мкм.
4.42. Определить длину волны фотона, импульс которого равен импульсу электрона, прошедшего разность потенциалов U = 9,8 В.
4.43. Определить температуру, при которой средняя энергия молекул трехатомного газа равна энергии фотонов, соответствующих излучению λ = 600 нм.
4.44. Определить, с какой скоростью должен двигаться электрон, чтобы его кинетическая энергия была равна энергии фотона, длина волны которого λ = 0,5 мкм.
4.45. Определить, с какой скоростью должен двигаться электрон, чтобы его импульс был равен импульсу фотона, длина волны которого λ = 2 пм.
4.46. Доказать, что световое давление, оказываемое на поверхность тела потоком монохроматического излучения, падающего перпендикулярно поверхности, в случае идеального зеркала равно 2 w, а в случае полностью поглощающей поверхности равно w, где w – объемная плотность энергии излучения.
4.47. Давление монохроматического света с длиной волны λ = 500 нм на зачерненную поверхность, расположенную перпендикулярно падающим лучам, равно 0,12 мкПа. Определить число фотонов, падающих ежесекундно на 1 м2 поверхности.
4.48. На идеально отражающую поверхность площадью S = 5 см2 за время t = 3 мин нормально падает монохроматический свет, энергия которого W = 9 Дж. Определить: 1) облученность поверхности; 2) световое давление, оказываемое на поверхность.
4.49. Определить давление света на стенки электрической 150-ваттной лампочки, принимая, что вся потребляемая мощность идет на излучение и стенки лампочки отражают 15 % падающего на них света. Считать лампочку сферическим сосудом радиуса 4 см.
4.50. Давление монохроматического света с длиной волны λ = 500 нм на зачерненную поверхность, расположенную перпендикулярно падающему излучению, равно 0,15 мкПа. Определить число фотонов, падающих на поверхность площадью 40 см2 за одну секунду.
4.51. Давление Р монохроматического света с длиной волны λ = 600 нм на зачерненную поверхность, расположенную перпендикулярно падающему излучению, составляет 0,1 мкПа. Определить: 1) концентрацию n фотонов в световом пучке; 2) число N фотонов, падающих ежесекундно на 1 м2 поверхности.
4.52. На идеально отражающую плоскую поверхность нормально падает монохроматический свет с длиной волны λ = 0,55 мкм. Поток излучения Фесоставляет 0,45 Вт. Определить: 1) число фотонов N, падающих на поверхность за время t = 3 с; 2) силу давления, испытываемую этой поверхностью.
4.53. Плоская световая волна интенсивностью I = 0,1 Вт/см2 падает под углом α = 30° на плоскую отражающую поверхность с коэффициентом отражения ρ = 0,7. Используя квантовые представления, определить нормальное давление, оказываемое светом на эту поверхность.
4.54. Рассматривая особенности механизма комптоновского рассеяния, объяснить: 1) почему длина волны рассеянного излучения больше, чем длина волны падающего излучения; 2) наличие в составе рассеянного излучения «несмещенной» линии.
4.55. Определить длину волны рентгеновского излучения, если при комптоновском рассеянии этого излучения под углом Θ = 60° длина волны рассеянного излучения оказалась равной 57 пм.
4.56. Фотон с энергией ε = 1,025 МэВ рассеялся на первоначально покоившемся свободном электроне. Определить угол рассеяния фотона, если длина волны рассеянного фотона оказалась равной комптоновской длине волны λс = 2,43 пм.
4.57. Узкий пучок монохроматического рентгеновского излучения падает на рассеивающее вещество. Оказывается, что длины волн рассеянного под углами Θ1 = 60° и Θ2 = 120° излучения отличаются в 1,5 раза. Определить длину волны падающего излучения, предполагая, что рассеяние происходит на свободных электронах.
4.58. Фотон с длиной волны λ = 5 пм испытал комптоновское рассеяние под углом Θ = 90° на первоначально покоившемся свободном электроне. Определить: 1) изменение длины волны при рассеянии; 2) энергию электрона отдачи; 3) импульс электрона отдачи.
4.59. Фотон с энергией ε = 0,25 МэВ рассеялся на первоначально покоившемся свободном электроне. Определить кинетическую энергию электрона отдачи, если длина волны рассеянного фотона изменилась на 20 %.
4.60. Фотон с энергией 0,3 МэВ рассеялся под углом Θ = 180° на свободном электроне. Определить долю энергии фотона, приходящуюся на рассеянный фотон.
4.61. Фотон с энергией 100 кэВ в результате комптоновского эффекта рассеялся при соударении со свободным электроном на угол Θ = π/2. Определить энергию фотона после рассеяния.
4.62. Фотон с энергией ε = 0,25 МэВ рассеялся под углом α = 120° на первоначально покоившемся свободном электроне. Определить кинетическую энергию электрона отдачи.
Date: 2016-05-24; view: 1095; Нарушение авторских прав