Применение подобия треугольников в измерительных работах

При решении многих задач на построение треугольников применяют так называемый метод подобия. Он состоит в том, что сначала на основании некоторых данных строят треугольник, подобный искомому, а затем, используя остальные данные, строят искомый треугольник.

Рассмотрим пример.

Задача:
Построить треугольник по данным двум углам и биссектрисе при вершине третьего угла.

Решение:
На рисунке изображены два данных угла и данный отрезок. Требуется построить треугольник, у которого два угла соответственно равны двум данным углам, а биссектриса равна данному отрезку.

Сначала построим какой-нибудь треугольник, подобный искомому. Для этого начертим произвольный отрезок АıВı и построим треугольник АıВıС, у которого углы Аı и Вı соответственно равны данным углам.

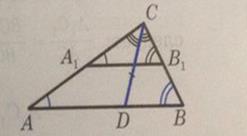
Далее построим биссектрису угла С и отложим на ней отрезок СD, равный данному отрезку. Через точку D проведем прямую, параллельную АıВı. Она пересекает стороны угла С в некоторых точках А и В. Треугольник АВС искомый.

В самом деле, так как АВ‖АıВı, то ∠А=∠Аı, ∠В=∠Вı, и, следовательно, два угла треугольника АВС соответственно равны данным углам. По построению биссектриса СD треугольника АВС равна данному отрезку. Итак, треугольник АВС удовлетворяет всем условиям задачи.

Очевидно, задача имеет решение, если сумма углов меньше 180°. Так как отрезок АıВı можно выбрать произвольно, то существует бесконечно много треугольников, удовлетворяющих условию задачи. Все эти треугольники равны друг другу, поэтому задача имеет единственное решение.

Date: 2016-05-23; view: 1632; Нарушение авторских прав