Построение окружности на местности

Для построения окружности на местности нам понадобится колышек и веревка. На местности устанавливается колышек, к которому привязывается верёвка. Держась за свободный конец верёвки и двигаясь вокруг колышка, можно описать окружность.

2.6. Практические способы построения параллельных прямых
Признаки параллельности прямых лежат в основе способов построения параллельных прямых с помощью различных инструментов, используемых на практике. Рассмотрим, например, способ построения параллельных прямых с помощью чертежного угольника и линейки.
Чтобы построить прямую, проходящую через точку М и параллельную данной прямой α, приложим чертежный угольник к прямой a, а к нему линейку так, как показано на рисунке.

Затем, передвигая угольник вдоль линейки, добьемся того, чтобы точка М оказалась на стороне угольника, и проведем прямую b. Прямые a и b параллельны, так как соответственные углы α и β равны.

На этом рисунке показан способ построения параллельных прямых при помощи рейсшины. Этим способом пользуются в чертежной практике.
Аналогичный способ применяется при выполнении солярных работ, где для разметри параллельных прямых используется малка (две деревянные планки, скрепленные шарниром).

Расстояние между параллельными прямыми.
Определение расстояния между двумя параллельными прямыми дается через расстояние от точки до прямой.

Расстояние между двумя параллельными прямыми – это расстояние от произвольной точки одной из параллельных прямых до другой прямой.

Для наглядности изобразим две параллельные прямые a и b, отметим на прямой а произвольную точку М₁, опустим перпендикуляр из точки М₁ на прямую b, обозначив его H₁. Отрезок М₁H₁ соответствует расстоянию между параллельными прямыми a и b.

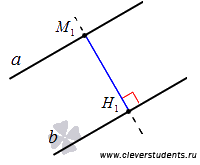
Приведенное определение расстояния между двумя параллельными прямыми справедливо как для параллельных прямых на плоскости, так и для прямых в трехмерном пространстве. Более того, такое определение расстояния между двумя параллельными прямыми принято не случайно. Оно тесно связано со следующей теоремой.
Теорема:
Все точки одной из двух параллельных прямых удалены на одинаковое расстояние от другой прямой.
Доказательство:
Рассмотрим параллельные прямые a и b. Отметим на прямой a точку М₁, опустим из нее перпендикуляр на прямую b. Основание этого перпендикуляра обозначим как H₁. Тогда длина перпендикуляра М₁H₁ есть расстояние между параллельными прямыми a и b по определению. Докажем, что равно , где М₂ – произвольная точка прямой a, отличная от точки M₁, а H₂ – основание перпендикуляра, проведенного из точки М₂ на прямую b. Доказав этот факт, мы докажем и саму теорему.

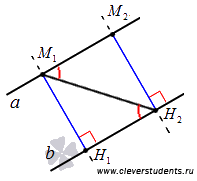
Так как внутренние накрест лежащие углы, образованные при пересечении двух параллельных прямых секущей, равны, то , а прямая M₂H₂, перпендикулярная прямой b по построению, перпендикулярна и прямой a. Тогда треугольники М₁H₁H₂ и М₂М₁H₂ прямоугольные, и, более того, они равны по гипотенузе и острому углу: М₁H₂ – общая гипотенуза, . Из равенства треугольников следует равенство их соответствующих сторон, поэтому, . Теорема доказана.
Следует заметить, что расстояние между двумя параллельными прямыми является наименьшим из расстояний от точек одной прямой до точек другой прямой.

Угловой отражатель

Мы знаем, что сумма двух острых углов прямоугольного треугольника равна 90°. Это свойство лежит в основе конструкции простейшего уголкового отражателя. Прежде чем описать его устройство, рассмотрим следующую задачу.
Задача:
Угол между зеркалами ОА и ОВ равен 90°. Луч света, падающий на зеркало ОА под углом α, отражается от него, а затем отражается от зеркала ОВ. Доказать, что падающий и отраженный лучи параллельны.

Решение:
По закону отражения света падающий луч SM и луч MN составляют с прямой ОА равные углы α. Так как треугольник MON прямоугольный, то угол MON равен 90°-α. Применяя опять закон отражения света, получаем, что луч MN и отраженный луч NT составляют с прямой ОВ равные углы. Обращаясь к рисунку, мы видим, что ∠SMN=180° - 2α, ∠MNT=180°-2(90°- α)=2α, поэтому ∠SMN+∠MNT=180°.
Следовательно, падающий луч SM и отраженный луч NT параллельны, что и требовалось доказать.

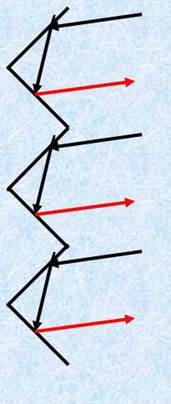
Простейший уголковый отражатель представляет собой несколько зеркал, составленных так, что соседние зеркала образуют угол в 90°. На рисунке в виде ломаной линии схематически изображен такой отражатель. Представим себе, что на этот отражатель падает пучок параллельных лучей. Тогда отраженные лучи будут параллельны падающим лучам.

Таким образом уголковый отражатель «возвращает назад» падающий на него пучок параллельных лучей при любом расположении отражателя по отношению к падающему пучку лучей.

Это свойство уголкового отражателя используется в технике. Так, уголковый отражатель устанавливается на заднем крыле велосипеда для того, чтобы «возвращать назад» свет автомобильных фар. Это дает возможность водитель автомобиля видеть ночью идущий впереди велосипед.

Date: 2016-05-23; view: 2257; Нарушение авторских прав