Основные законы измельчения

Обычно процесс измельчения изучается с двух позиций:

1. Выявляется зависимость между затратами энергии и степенью измельчения. Это позволяет выявить эффективность рабочего процесса, определить оптимальные рабочие органы применяемых типов машин и режимы их работы.

2. Определяется закономерность распределения измельченных частиц по крупности, что позволяет найти наиболее эффективные способы расчета средних размеров частиц, величин их удельной поверхности и численных значений степени измельчения.

Оба этих вопроса рассматриваются в энергетической теории измельчения.

Чтобы разрушить тело на части, необходимо приложить к нему усилие, большее, чем силы молекулярного сцепления. Силы молекулярного сцепления зависят от физико-механических свойств материала и поэтому могут быть различными. Работа внешних сил, затраченная на измельчение материала и отнесенная к единице массы или объема, называется удельной работой измельчения.

Еще в прошлом веке были предложены две энергетические теории измельчения: поверхностная и объемная. В соответствии с поверхностной теорией измельчения, которую предложил немецкий ученый П. Риттингер (1867 г.), работа измельчения прямо пропорциональна вновь образованной поверхности:

где α — коэффициент пропорциональности, учитывающий величину энергии молекулярного сцепления твердого тела.

Экспериментальные исследования показали, что поверхностная теория измельчения применима лишь при тонком измельчении. Для грубого измельчения русский ученый В.Л. Кирпичев (1874 г.) и немецкий ученый Ф. Кик (1885 г.) предложили объемную теорию измельчения, согласно которой работа измельчения прямо пропорциональна объему деформированной части тела

где k — коэффициент пропорциональности;

V — объем деформированной части тела.

Поскольку при измельчении могут получаться крупные и мелкие частицы, П.А. Ребиндер в 1928 г. предложил объединить обе теории в одну и рассматривать общую работу как сумму работ на образование новых поверхностей и деформацию, части объема тела

Анализируя приведенные зависимости, нетрудно убедиться, что для практического использования они малопригодны. С одной стороны, тяжело определить численные значения приращения поверхности и объема деформированной части тела, с другой — неизвестны коэффициенты a и k.

В 1952 г. С.В. Мельников предложил приближенную формулу для количественных расчетов работы измельчения в зависимости от степени измельчения:

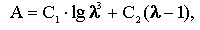
где С₁ и С₂ — коэффициенты, учитывающие удельные затраты энергии на измельчение и имеющие размерность удельной работы (Дж/ кг), определяются опытным путем. Например, для ячменя С₁ = (10...13) 103 Дж/ кг, С₂ = (6...9) 103 Дж/ кг.

Как мы уже говорили, при измельчении получаются частицы различного размера и тем более формы. Чтобы каким-то образом упорядочить размер и форму частиц для возможности дальнейших расчетов, принято приводить частицы неправильной формы к шару. При этом его диаметр определяется из фактического объема частицы неправильной формы. Определение объема частицы производят путем погружения отсчитанного их количества в мензурку с жидкостью, имеющий малый коэффициент поверхностного натяжения (керосин, ксилол, толуол и т.п.). Объем частицы определяется делением полученного общего объема на количество частиц в пробе

Тогда эквивалентный по объему диаметр частицы:

Было бы неправильным для определения эквивалентного диаметра брать частицы резко отличающихся размеров. А какие именно нужно брать?

В любом случае в массе измельченного материала размеры частиц подчиняются закону нормального распределения (закон Пуассона) (рис 5).

Этот график показывает, какой процент (или относительное количество) частиц имеет тот или иной размер. В любом случае частиц малого и большого размеров (диаметра) бывает меньше, чем среднего.

В зависимости от измельчающего рабочего органа кривая Пуассона может быть с высоким пиком или приплюснутая. Как оценить, каких частиц в массе материала больше? Для этого существуют различные методы определения среднего размера частиц: арифметический, геометрический, логарифмический, интегральный, взвешенный. Каждый из методов применим в определенных конкретных ситуациях.

Для практических условий наиболее пригоден метод определения средневзвешенного размера частиц. Это упрощенный среднеинтегральный метод. Если взять площадь под кривой и разделить на 100 % или Р, получим среднеинтегральный размер частиц. Но получить такую кривую сложно, да и обрабатывать ее трудоемко. Проще определить, сколько частиц данного размера находится в общей массе. Тогда получится гистограмма (рис 6).

По сути она описывается кривой нормального распределения, но получить ее и обработать значительно проще.

Берут навеску разноразмерного материала и просеивают ее на ситах с разным размером ячеек. Размер частиц от 0 до d₁ — проход через последнее сито, размер от d₁ до d₂ — остаток на последнем сите и т.д.

Размеры частиц остатка на первом сите обычно принимают равными:

где m — модуль сита — число, показывающее, насколько размер ячеек одного сита отличается от другого.

Как видно из гистограммы, средневзвешенный размер частиц можно определить по формуле:

Для зерновых кормов средневзвешенный размер частиц называется модулем помола.

В лабораторных анализах используют ситовой классификатор с набором из 10...12 сит с модулем m = 1,41 В производственных условиях используют классификатор из трех сит с размером ячеек 1, 2 и 3 мм. Тогда модуль помола:

где Р₀, Р₁, Р₂, Р₃ — процентное содержание фракций.

Для комбикормов принято считать М = 0,2...1 мм — мелкий помол, М = 1...1,8 — средний, М = 1,8...2,6 — крупный помол.

Date: 2016-05-23; view: 1353; Нарушение авторских прав