Бiр қалыпты айнымалы қозғалыс

Кез-келген бiрдей уақыт аралығында қозғалыс жылдамдығы сәйкес бiрдей шамаға өзгерiп отыратын қозғалысты бiр қалыпты айнымалы қозғалыс деп атайды.

Егер жылдамдық бiрдей шамаға артатын болса, онда қозғалысты бiр қалыпты үдемелi деп, ал егер жылдамдық бiрдей шамаға кемитiн болса, онда қозғалысты бiр қалыпты кемiмелi деп атайды. Олай болса, бiр қалыпты айнымалы қозғалыстар бiр-бiрiнен жылдамдықтың өзгеру шапшаңдығына қарай ажыратылады. Қозғалыстың осы қасиетiн сипаттау үшiн физикалық векторлық шама үдеу енгiзiлген.

Үдеу қозғалыс жылдамдығының өзгеруiнiң осы өзгерiс болып өткен уақытқа қатынасымен өлшенедi.Өлшем бірлігі .

Үдеудiң бағыты жылдамдықтың өзгерiсiнiң бағытына сәйкес келедi, сондықтан үдеу векторлық шама.

Үдеу жылдамдықтың уақыт бойынша бiрiншi туындысына немесе радиус вектордың уақыт бойынша екiншi туындысына тең болады.

.

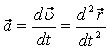Бiр қалыпты айнымалы қозғалыстың лездiк жылдамдығы

,

Ал қозғалыс теңдеуi

.

Жазық қозғалыс кезiнде дененiң үдеуiн нормаль және тангенциал деп аталатын екi құраушыға жiктейдi

.

Толық үдеудiң модулi: .

Жылдамдықтың модулi бойынша өзгеру шапшаңдығын сипаттайтын үдеу құраушысын тангенциал немесе жанама үдеу деп атайды.

.

Тангенциал үдеу траекторияға жанама бойымен бағытталады.

Дененiң жылдамдығының бағытының өзгеру шапшаңдығын сипаттайтын үдеудi нормаль үдеу деп атайды.

.

Жазық қозғалыс кезiндегi дененiң толық үдеуiнiң модулi:

.

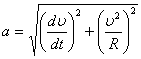Шеңбер бойымен бiр қалыпты қозғалыс

Дененiң шеңбер бойымен қозғалысын бұрыштық жылдамдықпен сипаттайды. Шеңбердiң центрiнен материялық нүктеге жүргiзiлген радиус осы уақыт iшiнде бұрыш сызады, оны бұрыштық ығысу мемесе бұрыштық орын ауыстыру деп атайды.

Бұрыштық жылдамдық бұрыштық орын ауыстырудың осы орын ауыстыруға кеткен уақытқа қатынасына тең. Өлшем бірлігі .

.

Бұрыштық жылдамдықтың бағыты бұрыштық орын ауыстырудың бағытымен сәйкес келедi.

Дененiң шеңбер бойымен бiр қалыпты қозғалысын сипаттау үшiн айналу жиiлiгi және периоды енгiзiлген.

Дененiң шеңбер бойымен толық айналымға кеткен уақытын айналу периоды деп айтады. Өлшем бірлігі .

,

мұндағы: уақыт ішінде жасалынатын N- айналым саны.

Айналу жиiлiгi деп дененiң айналу центрiнiң маңында бiр секунд iшiнде жасайтын айналым санын айтàды. Өлшем бірлігі .

.

Сөйтiп, период пен жиiлiктiң бiр-бiрiне керi шама екенiн байқаймыз.

периодқа тең уақытта бұрыштық орын ауыстыру -ге тең болады. Сондықтан бұрыштық жылдамдық немесе ескерсек, Шеңбер бойымен бiрқалыпты қозғалған дененiң сызықтық жылдамдығы модулi жағынан тұрақты, ал бағыты бойынша үздiксiз өзгерiп отырады және траекторияның кез-келген нүктесiне жүргiзiлген жанаманың бойымен бағытталады.Бiрқалыпты қозғалыс кезiнде сызықтық жылдамдықтың модулi тұрақты болғандықтан, оның шамасын мына формуламен анықтауға болады:

.

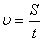Бiр айналым iшiнде (t=T) дене шеңбердiң доғасының ұзындығына тең ара қашықтықты жүрiп өтедi:

.

Сондықтан немесе екенiн ескерсек, .

Сызықтық және бұрыштық жылдамдықтар арасындағы байланыс: , яғни шеңбер бойымен бiрқалыпты қозғалыс кезiндегi сызықтық жылдамдық бұрыштық жылдамдықпен радиустың көбейтiндiсiне тең болады.

Динамика

Денелердiң өзара әсерлесуiн және осы әсерлесуден пайда болатын қозғалыстарды зерттейтiн механиканың бөлiмiн – динамика деп атайды. Динамиканың негiзiне 1687 жылы Ньютон тұжырымдаған қозғалыс заңдары жатады.

Date: 2016-05-18; view: 3732; Нарушение авторских прав