Колебание одномассовой системы при наличии жесткости

Расчетная схема колебаний одномассовой системы при наличии жесткости и отсутствии демпфирования приведена на рис.11.3.

Пусть имеется масcа m, опирающаяся на упругий элемент с жесткостью С_Р. В неподвижном состоянии вес Р = m×g уравновешивается силой сжатой пружины

,

где Z_cт – статический прогиб пружины.

Зададим массе m перемещение Z c ускорением . В результате чего возникает инерционная сила , направленная противоположно перемещению.

Перемещение массы на величину Z вызовет со стороны пружины дополнительную силу

.

Составим уравнение сил относительно вертикальной оси Z.

.

Если учесть, что имеем

.

После подстановки запишем

,

или .

Поскольку коэффициент при равен +1, поэтому выражение при Z принято 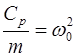, где w₀ – круговая частота собственных колебаний системы при отсутствии демпфирования в рад./с.

Частота колебаний в Гц запишется

Гц.

Если учесть, что жесткость упругого элемента соответствует , тогда окончательно частота собственных колебаний рассматриваемой системы равна

Гц, (11.2)

где Z_ст - статический прогиб упругого элемента в см.

Дифференциальное уравнение колебаний массы m имеет вид

. (11.3)

Это однородное дифференциальное уравнение второго порядка, общее решение которого будет

, (11.4)

где к_1, к₂ - корни характеристического уравнения.

Взяв производные с частного решения, имеем .

После подстановки этих значений в уравнение (11.4) получим характеристическое уравнение

.

Корни этого уравнения будут .

Подставив значения корней в уравнение (11.4) имеем

.

Воспользуемся преобразователем Эйлера

.

Тогда .

Для определения коэффициентов С ₁ и С ₂ зададимся начальными условиями.

При 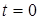, Z=Z_max.

При (T - период колебаний; Т= ; ; ; ), Z=0.

После подстановки имеем

при t=0 ; C₁=Z_max.

при ; ; С₂ =0.

Окончательно общее решение дифференциального уравнения . (11.5)

Формула (11.5) описывает незатухающие колебания при отсутствии демпфирования.

Рис. 11.4 График функции

Таким образом, при отсутствии демфирования возникают незатухающие колебания с частотой, которая будет зависеть только от статического прогиба упругого элемента.

Date: 2016-05-17; view: 476; Нарушение авторских прав