Картина эвольвентного зацепления

Построение картины внешнего эвольвентного зацепления   Пример построенной картины зацепления приведен на рисунке 13.     Рисунок 13 – Картина эвольвентного зацепления Построение картины эвольвентного зубчатого зацепления производится в следующем порядке: 1 Откладываем межосевое расстояние O1O2=αw/Kl, выбрав такой масштаб, чтобы получить LО1О2 = 850…900 мм.   2 Переводим расчетные диаметры окружностей в масштаб чертежа (поделив их значения на масштаб Kl) и определяем радиусы для вычерчивания этих окружностей.   3 Строим основные окружности с центрами в точках О1 и О2.   4 Проводим общую касательную N1N2 к основным окружностям и обозначаем полюс зацепления (W).   5 Проверяем радиусы начальных окружностей и строим эти окружности. 6 Проводим окружности вершин, находим точки пересечения с линией зацепления и определяем рабочий (активный) участок линии зацепления Р1Р2.   7 Проводим окружности впадин (радиус окружности впадин может быть больше, равен и меньше радиуса основной окружности. Это зависит от числа зубьев Z колеса и коэффициента смещения Х).   8 Строим эвольвенты, которые описывает точка (W) прямой N1N2 при перекатывании ее по основным окружностям: 1) отрезок N1W (N2W) делим на n равных частей и откладываем точно такие же части на основной окружности в обе стороны от точки N1 (N2). При этом в сторону полюса W откладывается n частей, в противоположную сторону (2-3 части);   2) полученные на основной окружности точки соединяем с центром колеса O1 (O2) и проводим в них касательные к основной окружности (перпендикуляры к соответствующим радиусам);   3) на касательных откладываем отрезки, включающие столько частей, сколько содержится в дуге основной окружности от точки касания до начала эвольвенты;   4) соединяя найденные на касательных точки, получим эвольвенту.   9 Откладываем толщину зуба (соответственно S1 и S2) на делительной окружности от построенной эвольвенты и, разделив эту толщину пополам, проводим ось симметрии зуба (она проходит через центр колеса О1 и О2 соответственно). По симметрии строим встречную эвольвенту зуба.   10 Начиная от граничной точки l   плавно сопрягаем эвольвенту с окружностью впадин. Так как по заданию не требуется точного построения переходной кривой, то сопряжение производится произвольной кривой.   11 Используя известный шаг по дуге делительной окружности (Р), строим соседние зубья. При этом можно использовать шаблоны. На каждом из колес должно быть изображено не менее 3-4 зубьев.   12 Отмечаем зону однопарного зацепления на линии зацепления, отложив основной шаг Pb (в выбранном масштабе Kl) от точек Р1 и Р2 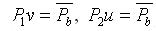  и проверяем графически коэффициент перекрытия: 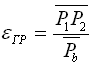  13 Отмечаем нижнюю точку Pi рабочего (активного) профиля зуба, для чего радиусом О1Р1 сносим точку Р1 на профиль зуба первого колеса – часть профиля от вершины зуба до точки Р1 является рабочей (активной) частью профиля зуба этого колеса. Аналогично отмечается рабочая часть профиля зуба второго колеса (точка Р2 сносится радиусом О2Р2 на профиль зуба этого колеса).   14 Отмечаем на профилях зубьев зону однопарного зацепления, для чего сносим точки u и v радиусами O1u и O1v – на профиль зуба первого колеса, а радиусами O2u и O2v – на профиль зуба второго колеса.   15 Обозначаем все расчетные диаметры (основных, делительных, начальных окружностей, а также окружностей вершин и впадин) в соответствии со стандартом.   16 На одном из колес отмечаем дугу зацепления на начальной окружности. Для этого строим эвольвенту зуба данного колеса в начале зацепления (проходящую через точку P1) и в конце зацепления данной пары (проходящую через точку P2). Дуга окружности между этими положениями эвольвенты является дугой зацепления на этой окружности (т.е. путь проходимый точкой зуба за время работы данной пары).   На рисунке 13 дуга cd представляет собой дугу зацепления на начальной окружности второго колеса (но дуга зацепления на начальной окружности первого равна дуге зацепления на начальной окружности второго колеса)

Date: 2016-05-17; view: 568; Нарушение авторских прав