Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Теоретические сведения к практической работе
|
|
Метод Эйлера.
Пусть требуется решить задачу Коши: найти решение дифференциального уравнения
(1)
удовлетворяющее начальному условию у(х0) = у0.
При численном решении дифференциального уравнения (1) задача ставится следующим образом: в точках х0, х0, х1, х2,...., хп найти приближения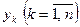 
для значений точного решения у(хк)
Разность 
называется шагом сетки. Во многих случаях величину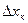 
принимают постоянной. Пусть 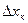= h, тогда
xk = x0 +kh где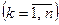 
(2)
Метод Эйлера основан на непосредственной замене производной разностным отношением по приближенной формуле
, где 
(3)
Приближенное значение ук в точке xk = x0 +kh вычисляется по формуле:
- формула Эйлера (4)
Пример 1: Методом Эйлера найти значения решения уравнения 
, для которого у(1) = 1, в пяти точках отрезка [ 1; 1,5 ], приняв h = 0,1
Решение. По формуле (2) находим точки х0 = 1, х1 = 1,1, х2 = 1,2, х3 = 1,3, х4 = 1,4, х5 = 1,5. Значения искомой функции у = у(х), удовлетворяющей условиям данной задачи Коши, вычисляем по формуле (4). Результаты вычислений занесем в таблицу.
| k | xk | yk | 2xk | f(xk , yk) = 2xk - yk | hf(xk , yk) = 0,1(2xk - yk) | yk+1 = yk + hf(xk , yk) |
| 1,0 | 1,0000 | 2,0 | 1,0000 | 0,1000 | 1,1000 | |
| 1,1 | 1,1000 | 2,2 | 1,1000 | 0,1100 | 1,2100 | |
| 1,2 | 1,2100 | 2,4 | 1,1900 | 0,1190 | 1,3290 | |
| 1,3 | 1,3290 | 2,6 | 1,2710 | 0,1271 | 1,4561 | |
| 1,4 | 1,4561 | 2,8 | 1,3439 | 0,1344 | 1,5905 | |
| 1,5 | 1,5905 | 3,0 | 1,4095 | 0,1410 | 1,7315 |
Метод Рунге – Кутта. (Один из наиболее употребляемых методов повышенной точности).
Пусть функция у определяется дифференциальным уравнением 
с начальным условием у(х0) = у0. При численном интегрировании такого уравнения по методу Рунге – Кутта определяются четыре числа:
(5)
Если положить 
, то можно доказать, что
.
Получаем следующую схему вычислений:
| x | Y | ki | Δy |
| x0 | y0 | k1 | 
|
| 
| k2 | |
|
| 
| k3 | |
| x0 + h | y0 + k3 | k4 | |
| x1 | y1 = y0 + Δy0 | k1 |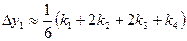 
|
| 
| k2 | |
|
| 
| k3 | |
| x1 + h | y1 + k3 | k4 | |
| x2 | y2 = y1 + Δy1 | k1 | 
|
| 
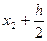
| k2 | |
|
| 
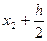
| k3 | |
| x2 + h | y2 + k3 | k4 | |
| .............. | ............. | .............. | ............... |
Пример 2:
Составь таблицу значений функции у, определяемой уравнением 
, при начальном условии у(0) = 1, 0 ≤ х ≤ 1 при h = 0,2.
Решение.
Используя формулы (5) найдем числа:
Отсюда 
Таким образом у1 = 1 + 0,1832 = 1,1832 при х = 0,2. По этой же схеме находим у2 и т.д. процесс вычисления ведем по схеме:
| x | Y | ki | Δy |
| x0 = 0 | y0 =1 | k1 = 0,2 |
= 0,1832
|
| = 0,1
| =1,1
| k2 = 0,1838 | |
| =0,1
| 1,0918
| k3 = 0,1817 | |
| x0 + h = 0,2 | y0 + k3 = 1,1817 | k4 = 0,1686 | |
| x1 = 0,2 | y1 = y0 + Δy0 = 1,1832 | k1 = 0,1690 |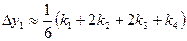
= 1,1584
|
| = 0,3
| = 1,2677
| k2 = 0,1589 | |
| = 0,3
| = 1,2626
| k3 = 0,1575 | |
| x1 + h = 0,4 | y1 + k3 = 1,3407 | k4 = 0,1488 | |
| x2 | y2 = y1 + Δy1 | k1 |
|
| .............. | ............. | .............. | ............... |
Содержание практической работы
1. Найти по методу Эйлера четыре значения функции у, определяемой уравнением 
, при начальном условии у(0) = 1, принимая h = 0,1.
| х | 0 | 0,1 | 0,2 | 0,3 | 0,4 |
| у | 1 | 1,1 | 1,22 | 1,36 | 1,52 |
Ответ:
2. По методу Рунге – Кутта проинтегрировать уравнение 
на промежутке [1; 2], при начальном условии у(1) = 0, принимая h = 0,1. В первых пяти точках.
Ответ:
| Х | 0 | 0,1 | 0,2 | 0,3 | 0,4 |
| У | -0,1158 | -0,1501 | -0,1925 | -0,2397 | -0,2944 |
3. По методу Рунге – Кутта проинтегрировать уравнение 
на промежутке [0; 1], при начальном условии у(0) = 1, принимая h = 0,1. Вычисление вести с тремя верными знаками.
Ответ:
| Х | 0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 |
| У | -1 | -0,975 | -0,949 | -0,921 | -0,888 | -0,842 | -0,802 | -0,744 | -0,675 | -0,593 | -0,495 |
Рекомендуемая литература
Основные источники
1. Григорьев С.Г., Иволгина С.В. Математика. – М.:Образовательно-издательский центр «Академия», 2011
2. Григорьев В.П., Сабурова Т.Н. Сборник задач по высшей математике. – М: Издательский центр «Академия», 2011
3. Богомолов Н.В. Практические занятия по математике. – М.: Высшая школа, 2010
4. Дадаян А.А. Математика: учеб.- М.: ФОРУМ: ИНФРА-М, 2012
Date: 2016-05-16; view: 524; Нарушение авторских прав