
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Цель: сформировать умение применять формулы интерполирования функции при решении задач
|
|
Интерполяционный полином Лагранжа.
Пусть дана таблица значений
| х | х1 | х2 | х3 | ............ | хп |
| у | у1 | у2 | у3 | ............ | уп |
Требуется составить полином (функцию) y = f (x) степени m ≤ n – 1, который принимал бы заданные значения yi при соответствующих значениях xi: yi = f (xi) (i = 1, 2, 3, ………n). Иными словами график функции должен проходить через заданные точки M (xi; yi)
Данная задача выполнима при использовании интерполяционного полинома Лагранжа:
 +
+
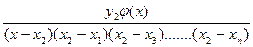 +......
+......
....+  (1)
(1)
или
 (2)
(2)
где 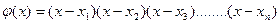 - вспомогательная функция п -й степени, в которой xi – заданные табличные значения аргумента.
- вспомогательная функция п -й степени, в которой xi – заданные табличные значения аргумента.
Пример 1: Составить полином Лагранжа, удовлетворяющий таблице значений
| х | ||||
| у |
Решение. Вспомогательная функция 
Вычислим 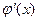 последовательно при данных значениях х:
последовательно при данных значениях х:
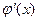 = (х - 2)(х - 3)(х - 4)+(х - 1)(х - 3)(х - 4)+(х - 1)(х - 2)(х - 4)+(х - 1)(х - 2)(х - 3);
= (х - 2)(х - 3)(х - 4)+(х - 1)(х - 3)(х - 4)+(х - 1)(х - 2)(х - 4)+(х - 1)(х - 2)(х - 3);
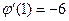 ,
,  ,
,  ,
, 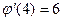 .
.
Тогда по формуле (1)
 == х + 1
== х + 1
Таким образом, в данном случае в качестве интерполяционного полинома найдена линейная функция f (x) = х + 1.
Интерполяционная формула Ньютона.
Пусть у0, у1, у2,....... – значения некоторой функции y = f (x), соответствующие равноотстоящим значениям аргументам х0, х1, х2,....... (т.е. хk+1 – xk = Δ x = const).
Введем обозначения:
Δ у0 = у1 – у0, Δ у1 = у2 – у1, Δ у2 = у3 – у2,........., Δ уп-1 = уп – уп-1 - разности первого порядка данной функции;
Δ2 у0 = Δ у1 – Δ у0, Δ2 у1 = Δ у2 – Δ у1,............. – разности второго порядка
........................................................................
Δ п+1у0 = Δ пу1 – Δ пу0, Δ п+1у1 = Δ пу2 – Δ пу1,............. – разности (п+ 1)- го порядка
Производя последовательные подстановки, получим:
Δ2 у0 = у2 -2у1 + у0, Δ3 у0 = у3 -3у2 +3 у1 – у0 ,........ 
Подобным же образом получаем:
у1 = у0 + Δ у0, у2 = у0 + 2 Δ у0 + Δ2 у0, у3 = у0 + 3 Δ у0 + 3 Δ2 у0 + Δ3 у0,......
 (3)
(3)
Запишем таблицу разностей:
х0 у0
Δ у0
х1 у1 Δ2 у0
Δ у1 Δ3 у0
х2 у2 Δ2 у1 Δ4 у0
Δ у2 Δ3 у1
х3 у3 Δ2 у2
Δ у3
х4 у4
....................................................
Если в формуле (3) положить, что п – не только целое и положительное число, а может быть любым п = t, то получим интерполяционную формулу Ньютона
 (4)
(4)
Мы получили такую функцию от t, которая обращается при t = 0 в у0, при t = 1 в у1 , при t = 2 в у2 и т. д. Поскольку последующее значение аргумента х при постоянном шаге h определяется формулой xn = x0 + nh, то  . Тогда, полагая x = x0 + th,
. Тогда, полагая x = x0 + th,  приведем формулу (3) к виду
приведем формулу (3) к виду  (3*)
(3*)
| х | |||||||
| у |
Пример 2:
Из таблицы
Найти значение у при х = 3,1, пользуясь интерполяционной формулой Ньютона.
Решение. Составим таблицу разностей:
| х | у | Δу | Δ2 у | Δ3 у |
Здесь х0 = 3, х = 3,1, h = 1. Тогда 
Интерполяционная формула Ньютона (4) для этого случая: 
Следовательно  , т.е. при х = 3,1 у = 13,71
, т.е. при х = 3,1 у = 13,71
Интерполяционная функция Ньютона (3*)  Содержание практической работы
Содержание практической работы
- Используя интерполяционную формулу Лагранжа, найти уравнение параболы проходящей через точки (2; 0), (4; 3), (6; 5), (8; 4), (10; 1).
(Ответ: у = 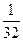 (х4 - 26х3 + 220х2 – 664х + 640))
(х4 - 26х3 + 220х2 – 664х + 640))
- Даны точки (0; 3), (2; 1), (3; 5), (4; 7). Используя интерполяционную формулу Лагранжа, составить уравнение функции, принимающей указанные значения при заданных значениях аргумента.
(Ответ: у =  (- 2х3 -15х2 + 25х -9))
(- 2х3 -15х2 + 25х -9))
- Используя интерполяционную формулу Лагранжа, построить функцию, принимающую значения заданные таблицей.
| х | ||||
| у | -7 |
(Ответ: у =  (х3 -13х2 + 69х -92))
(х3 -13х2 + 69х -92))
- Используя интерполяционную формулу Лагранжа, построить функцию, график которой проходит через точки (2; 3), (4; 7), (5; 9), (10; 19).
(Ответ: у =2х - 1)
- Найти интерполяционный полином Ньютона для функции y = f (x), если известныее значения f (1) = 6, f (3) = 24, f (4) =45.
(Ответ: у = 4х2 - 7х+ 9)
- Найти интерполяционный полином Ньютона для функции f(x)= 2x и ее значениям в точках х0 = -1, х1 = 0, х2 = 1, х3 = 2, х4 = 3 ивычислить f(-0,5) и f(2,5).
(Ответ: у =8 + 4(х - 3) + (х – 3)(х - 2)+  (х – 3)(х - 2)(х – 1) +
(х – 3)(х - 2)(х – 1) + 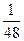 (х – 3)(х - 2)(х – 1)х, f(-0,5)= 0,700, f(2,5)= 5,658.)
(х – 3)(х - 2)(х – 1)х, f(-0,5)= 0,700, f(2,5)= 5,658.)
Практическая работа №25
Date: 2016-05-16; view: 622; Нарушение авторских прав