Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Вихідні та розрахункові дані для обчислення показників варіації інтервального ряду
|
|
| Групи господарств | Кількість господарств ni | Середина інтервалу хі | xi∙ni | │xi-`x│ni | (xi-`x)2 ni |
| 25-28 | 26,5 | 291,5 | 26,4 | 63,36 | |
| 28-31 | 29,5 | 3,6 | |||
| 31-34 | 32,5 | 7,2 | 25,92 | ||
| 34-37 | 35,5 | 13,2 | 87,12 | ||
| Разом | х | 722,5 | 52,8 |
Визначимо показники варіації для результативної ознаки Y:
- Середнє лінійне відхилення:
= 
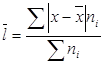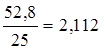
- Дисперсія:
= 
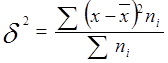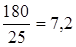
- Середнє квадратичне відхилення:
= 
.
- Розмах варіації:
R = хmax - xmin = 35,5-26,5=9
Розрахуємо коефіцієнти варіації:
v R= 
∙100% 
31,14%
v ` l = 
∙100% = 7,308%
v δ =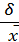 
∙100% = 9,304%
Оскільки v δ = 9,304%, і 9,304% < 33,%, то дана сукупність однорідна.
Дисперсія має ряд математичних властивостей, які спрощують її розрахунки:
ü Якщо до всіх значень варіюючої ознаки додати або відняти одне й теж число, то дисперсія не зміниться.
ü Якщо до всі значення зменшити або збільшити в якесь с число разів, то дисперсія зміниться в 
разів.
ü Дисперсія відносно середньої величини буде завжди менша ніж дисперсія будь-якої величини а, при а≠ 
.
ü Дисперсія постійної величини дорівнює нулю.
Таблиця 8
Date: 2016-05-15; view: 492; Нарушение авторских прав