
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Вихідні та розрахункові дані для обчислення середньої арифметичної
|
|
| Групи за рівнем урожайності | Кількість господарств ni | Середина інтервалу хi | Нагромаджена частота | xi×ni | 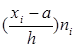
|
| 25-28 | 26,5 | 291,5 | |||
| 28-31 | 29,5 | ||||
| 31-34 | 32,5 | ||||
| 34-37 | 35,5 | ||||
| Разом | Х | X | 722,5 |
Обчислимо середню арифметичну звичайним способом:
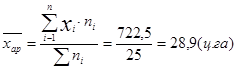
Для розрахунку середньої арифметичної способом моментів результати обчислень, наведених у таблиці, підставляємо у формулу:
m1= 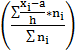 =
=  0,8
0,8  m1h + а = 0,8∙3+26,5 = 28,9 ц. га
m1h + а = 0,8∙3+26,5 = 28,9 ц. га
Середніми величинами в статистичних рядах розподілу є мода і медіана, які відносяться до класу структурних середніх. їх величини залежать лише від характеру частот, тобто від структури розподілу. На відміну від інших середніх, які залежать від усіх значень ознаки, мода і медіана не залежить від крайніх значень.
Мода (Мо) — це значення варіанти, що найчастіше повторюється в ряду розподілу. Для інтервального ряду розподілу мода обчислюється за такою формулою:
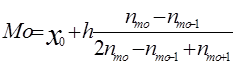 ,
,
де х0 – мінімальна межа модального інтервалу, h – розмір модального інтервалу, nmo-1 – частота інтервалу, що передує модальному, nmo– частота модального інтервалу, nmo+1– частота інтервалу, що стоїть за модальним.
Медіаною (Мe) називають варіанту, що ділить ранжирований ряд на дві рівні за обсягом частини. В інтервальному ряду розподілу медіана визначається за формулою:
Ме=  ,
,
де х0 – мінімальна межа медіанного інтервалу; h- величина медіанного інтервалу; - півсума частот (половина одиниць сукупності); SMe-1- сума нагромаджених частот, що стоять перед медіанним інтервалом; nMe – частота медіанного інтервалу.
Визначимо моду і медіану для результативної ознаки (урожайності):
Мо(Y)= 25 +3  = 28 ц. га;
= 28 ц. га;
Ме(Y)=  =28,408 ц. га.
=28,408 ц. га.
Середня арифметична має ряд властивостей.
ü якщо кожне значення варіанти поділити або помножити на певне число, то середня арифметична величина зменшиться або збільшиться у теж саме число разів.;
ü якщо до кожного значення варіюючої ознаки додати або відняти якесь число, то середня арифметична величина збільшиться або зменшиться на теж саме число;
ü якщо усі частоти поділити (або помножити) на якесь число, то середня арифметична величина не зміниться.;
ü середня арифметична постійної величини дорівнює цій постійній;
ü алгебраїчна сума відхилень окремих варіант ознаки від середньої дорівнює нулю.
Перевіримо властивості середньої арифметичної для результативної ознаки.
Таблиця 6
Date: 2016-05-15; view: 807; Нарушение авторских прав