Методические указания. 1. Общая схема методов поиска минимума на отрезке

1. Общая схема методов поиска минимума на отрезке

Пусть функция унимодальна на отрезке (т.е. имеет только один минимум). Необходимо найти точку минимума функции на этом отрезке с заданной точностью . Все методы одномерного поиска строятся на последовательном уменьшении интервала, содержащего точку минимума.

Возьмем внутри отрезка две точки и : ,

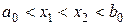и вычислим значения функции в этих точках. Из свойства унимодальности функции можно сделать вывод о том, что минимум расположен либо на отрезке , либо на отрезке . Действительно, если , то минимум не может находиться на отрезке , а если 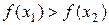, то минимум не может находиться на отрезке . Если же , то минимум находится на интервале .

Алгоритм заканчивается, когда длина интервала, содержащего минимум, становится меньше . Различные методы одномерного поиска отличаются выбором точек . Обычно сравнивают число вычислений функции, необходимое для достижения заданной точности.

2. Метод дихотомии (деления отрезка пополам)

Точки выбираются на расстоянии 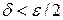от середины отрезка:

(1)

За одну итерацию интервал неопределенности уменьшается примерно в два раза (рис. 1). За итераций длина интервала будет примерно равна . Для достижения точности потребуется 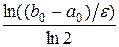итераций. На каждой итерации функция вычисляется два раза.

Рис. 1. Метод дихотомии

2. Метод золотого сечения

Точки находятся симметрично относительно середины отрезка и делят его в пропорции золотого сечения, т.е. когда длина всего отрезка относится к длине большей его части также, как длина большей части относится к длине меньшей части:

и

Отсюда

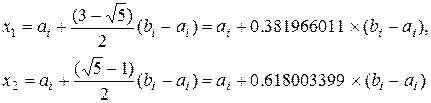(2)

За одну итерацию интервал неопределенности уменьшается в раз, но на следующей итерации мы будем вычислять функцию только один раз, так как по свойству золотого сечения и . (рис. 2). Для достижения точности потребуется итераций.

Неточное задание величины на ЭВМ уже при достаточно небольшом количестве итераций может приводить к погрешностям и потере точки минимума, так как она выпадает из интервала неопреде­ленности. Поэтому, вообще говоря, при реализации алгоритма возможность такой ситуации должна быть предусмотрена.

Рис. 2. Метод золотого сечения

3. Метод Фибоначчи

Числа Фибоначчи определяются соотношениями:

.

С помощью индукции можно показать, что -е число Фибоначчи представимо в виде (формула Бинэ):

Из этой формулы видно, что при больших : так что числа Фибоначчи с увеличением растут очень быстро.

На начальном интервале вычисляют точки

(3)

где выбирается по формуле (5), исходя из точности и начальной длины интервала.

На -м шаге метода будет получена тройка чисел , локализирующая минимум , такая, что

а точка с вычисленным значением

,

совпадает с одной из точек

(4)

расположенных на отрезке симметрично относительно его середины (рис. 3). При процесс заканчивается. В этом случае длина отрезка

а точки

совпадают и делят отрезок пополам.

Рис. 3. Метод Фибоначчи

Следовательно

.

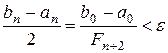Отсюда можно выбрать из условия

. (5)

С ростом , из-за того, что – бесконечная десятичная дробь, происходит искажение метода. Поэтому на очередном шаге в качестве новой точки берут из (4) наиболее удалённую от на предыдущем шаге.

4. Поиск минимума функции на прямой

В рассмотренных методах требуется знать начальный отрезок, содержащий точку минимума. Поиск на прямой заключатся в том, что осуществляются возрастающие по величине шаги, до тех пор, пока не будет пройдена точка минимума функции, т.е. убывание функции сменится на возрастание.

На первом шаге выбираем начальную точку 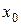и определяем направление убывания функции.

Шаг 1. Если , то полагаем , . Иначе, если , то , .

Шаг 2. Удваиваем и вычисляем .

Шаг 3. Если , то полагаем и переходим к шагу 2. Иначе – поиск прекращаем, т.к. отрезок 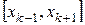содержит точку минимума.

5. Поиск минимума функции n переменных в заданном направлении

Пусть требуется найти минимум функции n переменных , где , в направлении вектора . Для этого нужно найти минимум функции 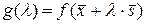рассмотренными выше методами, – величина шага в заданном направлении.

Date: 2016-05-15; view: 754; Нарушение авторских прав