При распространении упругой волны частицы среды совершают колебания около положения равновесия. Переноса вещества среды из одного места в другое не происходит

Фронт волны – геометрическое место точек среды, до которых в данный момент времени дошел волновой процесс.

Волновая поверхность – геометрическое место точек среды, колеблющихся в одинаковой фазе.

Луч – линия, касательная к которой в каждой точке совпадает с направлением распространения волны (в однородной изотропной среде луч – прямая, перпендикулярная к фронту волны и совпадающая с направлением переноса энергии волны).

Плоская волна – волна, в которой волновые поверхности представляют собой плоскости, перпендикулярные к направлению распространения волны.

Сферическая волна – волна, в которой волновые поверхности представляют собой сферы.

Два вида упругих волн в среде: 1) продольные; 2) поперечные.

Продольная механическая волна – волна, в которой частицы среды колеблются в направлении ее распространения (возникает в результате деформации сжатия - разрежения).

Поперечная механическая волна – волна, в которой частицы среды колеблются в направлении, перпендикулярном направлению ее распространения (возникает в результате деформации сдвига).

Продольные механические волны распространяются в газообразных, жидких и твердых средах.

Поперечные механические волны могут распространяться в жидкости только в одном случае – на ее поверхности. Но в возникновении этих волн принимают участие не силы упругости, а либо сила тяжести, либо силы поверхностного натяжения.

Скорость распространения волны (фазовая скорость) – физическая величина, равная расстоянию, которое за единицу времени проходит любая точка волновой поверхности (определяется упругими свойствами среды).

Скорость распространения энергии волны от источника конечна и не может превышать скорость света в вакууме (на фазовую скорость это ограничение не распространяется).

Длина волны (λ) – кратчайшее расстояние между двумя точками среды, колеблющимися в одинаковой фазе (определяется упругими свойствами среды).

Период волны (Т) – время одного полного колебания частицы среды около положения равновесия (определяется колебаниями источника волны).

Частота (ν) – физическая величина, показывающая, сколько полных колебаний совершает частица среды в единицу времени (определяется колебаниями источника волны).

Формула, связывающая длину волны, скорость ее распространения и период:

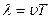, где 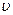– скорость волны.

Формула, связывающая скорость волны, ее длину и частоту: 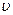= λν.

Отставание (по времени) колебаний точек среды, удаленных от источника волны на расстояние ∆x: .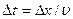

Разность фаз ∆φ колебаний двух точек среды, отстоящих друг от друга на расстоянии ∆x, взятом вдоль луча, определяется выражением: ,где λ – длина волны.

Уравнение плоской синусоидальной волны, распространяющейся вдоль координатной оси х:

, где S – смещение точки среды, удаленной от источника волны на расстояние Δx, в данный момент времени, S_m – амплитуда колебаний частиц среды в волне, ω=2πν – циклическая частота колебаний частиц среды, k = 2π/λ – волновое число, φ_o – начальная фаза колебаний.

Волновое число – число, показывающее, сколько длин волн укладывается на отрезке 2π единиц длины.

Формула для расчета объемной плотности энергии волны: 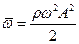,где ρ – плотность вещества, в котором распространяется волна, ω – циклическая частота колебаний частиц среды в волне, А – амплитуда колебаний частиц среды.

Формула для расчета интенсивности волны (энергии, переносимой волной в среднем в единицу времени через единицу площади поверхности, перпендикулярной к направлению ее распространения): ,где – объемная плотность энергии волны, 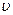– скорость волны, ρ – плотность среды, ω – циклическая частота колебаний частиц среды в волне, А – амплитуда колебаний частицы среды.

Уравнение сферической синусоидальной волны, распространяющейся в среде:

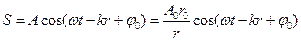, где S – значение смещения частицы среды из положения равновесия в данный момент времени, А_о – амплитуда колебаний источника волны, А – амплитуда колебаний частицы среды, r – расстояние от данной точки среды до центра сферического источника волны, r_о – радиус сферического источника волны, k – волновое число, ω – циклическая частота колебаний, φ_o – начальная фаза колебаний.

В непоглощающей энергию среде интенсивность плоской волны остается неизменной; интенсивность сферической волны убывает по закону: , где І_o – интенсивность источника волны, r_о – радиус источника волны, r – расстояние от данной точки среды до центра источника волны.

Date: 2016-06-09; view: 656; Нарушение авторских прав